▷ Résoudre l'indétermination zéro entre zéro (0/0)

Dans cet article, nous expliquons comment sauvegarder la limite d’une fonction lorsqu’elle donne l’incertitude 0/0. De plus, vous pourrez vous entraîner avec des exercices résolus sur l’indétermination de zéro entre zéro.

Comment résoudre l’indétermination zéro entre zéro (0/0)

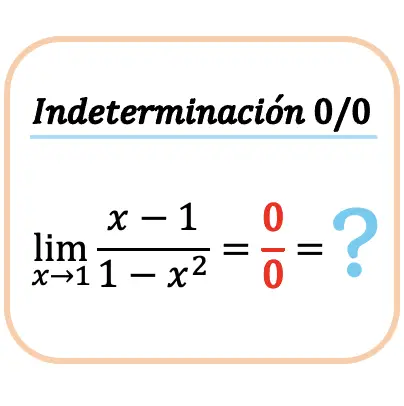
Nous verrons ensuite comment calculer la limite d’une fonction lorsqu’elle donne l’indétermination zéro entre zéro (0/0). Pour ce faire, nous allons calculer un exemple étape par étape :

$\displaystyle\lim_{x \to 2} \frac{x^2-x-2}{x^2-3x+2}$

Nous essayons d’abord de calculer la limite en substituant la valeur de x dans la fonction :

$\displaystyle\lim_{x \to 2} \frac{x^2 - x -2}{x^2-3x+2}=\frac{2^2 -2-2}{2^2-3\cdot 2+2}=\frac{0}{0}$

Mais on obtient l’indétermination 0 divisé par 0.

Lorsque la limite d’une fonction en point donne l’ incertitude 0/0 , il faut factoriser les polynômes du numérateur et du dénominateur puis simplifier les facteurs communs.

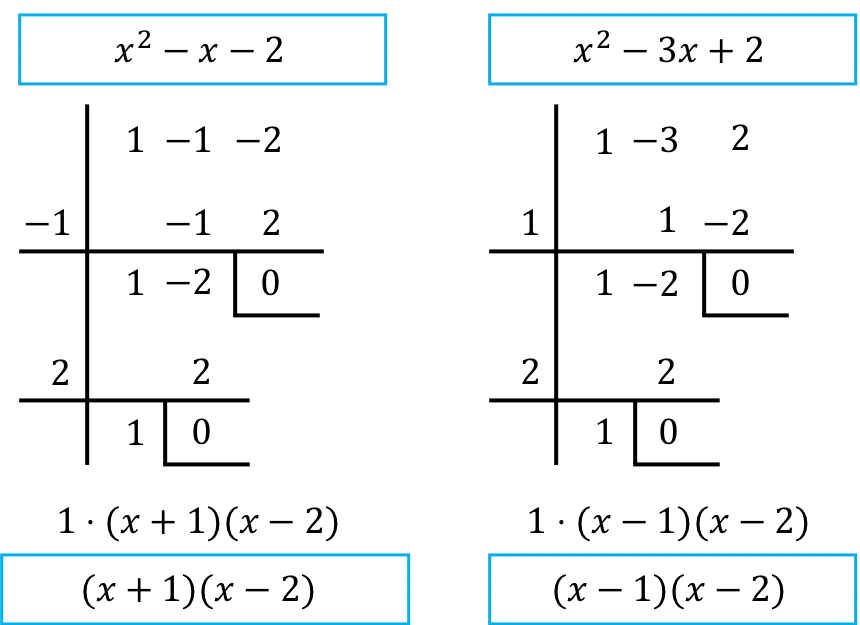
Il faut donc factoriser les polynômes du numérateur et du dénominateur de la fraction. Pour ce faire, nous utilisons la règle de Ruffini :

➤ Si vous ne savez pas factoriser un polynôme , nous vous recommandons de voir l’explication sur notre site spécialisé en polynômes : www.polinomios.org

Ainsi, une fois les polynômes factorisés, la limite est la suivante :

$\displaystyle\lim_{x \to 2} \cfrac{x^2-x-2}{x^2-3x+2}=\lim_{x \to 2}\frac{(x+1)(x-2)}{(x-1)(x-2)}$

Nous pouvons maintenant simplifier la limite en éliminant les facteurs qui se répètent au numérateur et au dénominateur de la fraction :

$\displaystyle\lim_{x \to 2} \cfrac{(x+1)\cancel{(x-2)}}{(x-1)\cancel{(x-2)}}=\lim_{x \to 2} \cfrac{(x+1)}{(x-1)}$

Et enfin, on recalcule la limite :

$\displaystyle\lim_{x \to 2} \cfrac{x+1}{x-1}=\cfrac{2+1}{2-1}=\cfrac{3}{1}=\bm{3}$

Comme vous pouvez le constater, une fois que nous avons factorisé et simplifié les polynômes, il est très facile de trouver la solution à la limite.

Indétermination 0/0 avec racines

Nous venons de voir comment se résolvent les indéterminations 0/0 des fonctions rationnelles. Cependant, si la limite est d’une fonction irrationnelle (ou radicale), l’indétermination 0/0 se résout différemment.

$\displaystyle\lim_{x \to 1} \frac{x-1}{\sqrt{x}-1}$

Tout d’abord, nous essayons de résoudre la limite en effectuant les opérations :

$\displaystyle\lim_{x \to 1} \frac{x-1}{\sqrt{x}-1}=\frac{1-1}{\sqrt{1}-1}=\frac{0}{0}$

Mais nous obtenons l’indétermination zéro sur zéro.

Si la limite d’une fonction avec racines donne l’indétermination 0/0 , il faut multiplier le numérateur et le dénominateur de la fraction par le conjugué de l’expression radicale.

➤ N’oubliez pas que le conjugué est la même expression irrationnelle mais avec le signe du milieu modifié.

Ensuite, on multiplie à la fois le numérateur et le dénominateur de la fraction par le conjugué de l’expression radicale :

$\displaystyle\lim_{x \to 1} \frac{\left(x-1\right)\cdot\left(\sqrt{x}+1\right)}{\left(\sqrt{x}-1\right)\cdot\left(\sqrt{x}+1\right)}$

Dans ce type de limites, en faisant cette étape on obtiendra toujours une identité notable que l’on pourra simplifier. Dans ce cas, au dénominateur on a le produit d’une somme et d’une différence, donc :

$\displaystyle\lim_{x \to 1} \frac{\left(x-1\right)\cdot\left(\sqrt{x}+1\right)}{\left(\sqrt{x}\right)^2-1^2}$

$\displaystyle\lim_{x \to 1} \frac{\left(x-1\right)\cdot\left(\sqrt{x}+1\right)}{x-1}$

Nous simplifions le facteur qui est répété au numérateur et au dénominateur :

$\displaystyle\lim_{x \to 1} \frac{\cancel{\left(x-1\right)}\cdot\left(\sqrt{x}+1\right)}{\cancel{x-1}}=\lim_{x \to 1}\left(\sqrt{x}+1\right)$

Et de cette façon on peut trouver le résultat de la limite :

$\displaystyle\lim_{x \to 1}\left(\sqrt{x}+1\right)=\sqrt{1}+1=2$

Exercices résolus sur l’indétermination 0/0

Ci-dessous, nous avons préparé plusieurs exercices résolus étape par étape sur les limites de fonctions qui donnent des indéterminations 0/0. Vous pouvez essayer de les faire, puis vérifier la solution.

N’oubliez pas que vous pouvez nous poser toutes vos questions sur la résolution des limites dans les commentaires !

Exercice 1

Calculez la limite de la fonction rationnelle suivante au point x=-2.

$\displaystyle\lim_{x \to -2}\frac{x^2 +2x}{x^2-x-6}$

Voir la solution

Logiquement, nous essayons d’abord de résoudre la limite :

$\displaystyle\lim_{x \to -2} \frac{x^2 +2x}{x^2-x-6}=\frac{(-2)^2+2\cdot (-2)}{(-2)^2-(-2)-6}=\frac{4-4}{4+2-6}=\frac{0}{0}$

Mais on se retrouve avec l’indétermination 0/0. Il faut donc factoriser les polynômes du numérateur et du dénominateur :

$\displaystyle\lim_{x \to -2}\frac{x^2 +2x}{x^2-x-6}=\lim_{x \to -2}\frac{x(x+2)}{(x+2)(x-3)}$

Maintenant, nous simplifions la fraction en supprimant les parenthèses qui sont répétées au numérateur et au dénominateur :

$\displaystyle\lim_{x \to -2}\frac{x\cancel{(x+2)}}{\cancel{(x+2)}(x-3)}=\lim_{x \to -2}\frac{x}{x-3}$

Et enfin, on recalcule la limite avec la fraction simplifiée :

$\displaystyle\lim_{x \to -2}\frac{x}{x-3}=\cfrac{-2}{-2-3}=\cfrac{-2}{-5}=\mathbf{\cfrac{2}{5}}$

Exercice 2

Résolvez la limite de la fonction suivante lorsque x tend vers -1 :

$\displaystyle\lim_{x \to -1}\frac{x^3+2x^2-x-2}{x^3-5x^2+2x+8}$

Voir la solution

Nous essayons d’abord de résoudre la limite comme d’habitude :

$\displaystyle\lim_{x \to -1}\frac{x^3+2x^2-x-2}{x^3-5x^2+2x+8}=\frac{(-1)^3+2(-1)^2-(-1)-2}{(-1)^3-5(-1)^2+2(-1)+8} =\frac{0}{0}$

Mais on obtient l’indétermination 0 entre 0. Il faut donc factoriser les 2 polynômes de la fraction :

$\displaystyle\lim_{x \to -1}\frac{x^3+2x^2-x-2}{x^3-5x^2+2x+8}=\lim_{x \to -1}\frac{(x-1)(x+1)(x+2)}{(x+1)(x-2)(x-4)}$

Nous pouvons maintenant simplifier les polynômes :

$\displaystyle\lim_{x \to -1}\frac{(x-1)\cancel{(x+1)}(x+2)}{\cancel{(x+1)}(x-2)(x-4)}=\lim_{x \to -1}\frac{(x-1)(x+2)}{(x-2)(x-4)}$

Et on résout la limite :

$\displaystyle\lim_{x \to -1} \frac{(x-1)(x+2)}{(x-2)(x-4)}=\frac{ (-1-1)(-1+2)}{(-1-2)(-1-4)}=\frac{(-2)\cdot (1)}{(-3)\cdot (-5)}=\frac{\bm{-2}}{\bm{15}}$

Exercice 3

Déterminer la solution de la limite de la fonction radicale suivante :

$\displaystyle\lim_{x\to 2}\frac{x^2-3x+2}{2-\sqrt{2x}}$

Voir la solution

Tout d’abord, nous vérifions si la limite donne une sorte d’indétermination :

$\displaystyle\lim_{x\to 2}\frac{x^2-3x+2}{2-\sqrt{2x}}=\frac{2^2-3\cdot2+2}{2-\sqrt{2\cdot 2}}=\frac{4-6+2}{2-2}=\frac{0}{0}$

La limite donne l’indétermination zéro divisé par zéro et on a une racine dans la fonction. Il faut donc multiplier le numérateur et le dénominateur de la fraction par le conjugué de l’expression radicale :

$\displaystyle\lim_{x\to 2}\frac{\left(x^2-3x+2\right)\cdot \left(2+\sqrt{2x}\right)}{\left(2-\sqrt{2x}\right)\cdot \left(2+\sqrt{2x}\right)}$

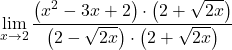
Le dénominateur correspond au développement de l’identité notable du produit d’une somme et d’une différence, on peut donc le simplifier :

$\displaystyle\lim_{x\to 2}\frac{\left(x^2-3x+2\right)\cdot \left(2+\sqrt{2x}\right)}{2^2-\left(\sqrt{2x}\right)^2}$

$\displaystyle\lim_{x\to 2}\frac{\left(x^2-3x+2\right)\cdot \left(2+\sqrt{2x}\right)}{4-2x}$

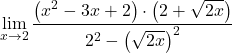
Cependant, nous ne pouvons pas encore simplifier les termes de la fraction. Il faut donc factoriser les polynômes :

$\displaystyle\lim_{x\to 2}\frac{\left(x^2-3x+2\right)\cdot \left(2+\sqrt{2x}\right)}{4-2x}=\lim_{x\to 2}\frac{(x-1)(x-2)\cdot\left(2+\sqrt{2x}\right)}{-2(x-2)}$

De cette façon, nous pouvons simplifier la fraction :

$\displaystyle\lim_{x\to 2}\frac{(x-1)\cancel{(x-2)}\left(2+\sqrt{2x}\right)}{-2\cancel{(x-2)}}=\lim_{x\to 2}\frac{(x-1)\left(2+\sqrt{2x}\right)}{-2}$

Et maintenant nous pouvons déterminer le résultat de la limite :

$\displaystyle\lim_{x\to 2}\frac{(x-1)\left(2+\sqrt{2x}\right)}{-2}=\frac{(2-1)\left(2+\sqrt{2\cdot 2}\right)}{-2}=\frac{1\cdot (2+2)}{-2}=\bm{-2}$

Exercice 4

Calculez la limite lorsque x tend vers 0 de la fonction radicale suivante :

$\displaystyle\lim_{x\to 0}\frac{x^2+6x}{3-\sqrt{4x+9}}$

Voir la solution

Tout d’abord, nous essayons de calculer la limite de la fonction comme nous le faisons toujours :

$\displaystyle\lim_{x\to 0}\frac{x^2+6x}{3-\sqrt{4x+9}}=\frac{0+0}{3-\sqrt{4\cdot 0+9}}=\frac{0}{3-3}=\frac{0}{0}$

Mais nous obtenons la forme indéterminée de 0/0. Par conséquent, on multiplie le numérateur et le dénominateur de la fonction par le conjugué de l’expression irrationnelle :

$\displaystyle\lim_{x\to 0}\frac{\left(x^2+6x\right)\cdot\left(3+\sqrt{4x+9}\right)}{\left(3-\sqrt{4x+9}\right)\cdot\left(3+\sqrt{4x+9}\right)}$

Nous appliquons la formule d’identité notable correspondante pour simplifier le dénominateur :

$\displaystyle\lim_{x\to 0}\frac{\left(x^2+6x\right)\cdot\left(3+\sqrt{4x+9}\right)}{3^2-\left(\sqrt{4x+9}\right)^2}$

$\displaystyle\lim_{x\to 0}\frac{\left(x^2+6x\right)\cdot\left(3+\sqrt{4x+9}\right)}{9-(4x+9)}$

$\displaystyle\lim_{x\to 0}\frac{\left(x^2+6x\right)\cdot\left(3+\sqrt{4x+9}\right)}{-4x}$

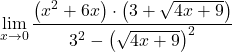
Maintenant, nous factorisons le binôme du numérateur en prenant le facteur commun :

$\displaystyle\lim_{x\to 0}\frac{\left(x^2+6x\right)\cdot\left(3+\sqrt{4x+9}\right)}{-4x}=\lim_{x\to 0}\frac{\bigl[x(x+6)\bigr]\cdot\left(3+\sqrt{4x+9}\right)}{-4x}$

Nous simplifions les facteurs qui sont répétés au numérateur et au dénominateur de la fonction :

$\displaystyle\lim_{x\to 0}\frac{\cancel{x}\left(x+6\right)\left(3+\sqrt{4x+9}\right)}{-4\cancel{x}}=\lim_{x\to 0}\frac{(x+6)\left(3+\sqrt{4x+9}\right)}{-4}$

Et, pour finir, on résout la limite de la fonction :

$\begin{array}{l}\displaystyle\lim_{x\to 0}\frac{(x+6)\left(3+\sqrt{4x+9}\right)}{-4}=\\[3ex]\displaystyle=\frac{(0+6)\left(3+\sqrt{4\cdot 0+9}\right)}{-4}=\\[3ex]\displaystyle=\frac{6\cdot (3+3)}{-4}=\frac{36}{-4}=\bm{-9}\end{array}$

Exercice 5

Résolvez la limite suivante en appliquant la méthode d’indétermination 0/0 :

$\displaystyle\lim_{x \to -1}\frac{x^3+2x^2-x-2}{x^3+5x^2+7x+3}$

➤ Voir : comment calculer les limites latérales d’une fonction

Voir la solution

Nous essayons d’abord de résoudre la limite :

$\displaystyle\lim_{x \to -1}\frac{x^3+2x^2-x-2}{x^3+5x^2+7x+3}=\frac{(-1)^3+2(-1)^2-(-1)-2}{(-1)^3+5(-1)^2+7(-1)+3}=\frac{0}{0}$

Mais à la limite on obtient l’indétermination zéro sur zéro. Par conséquent, nous factorisons les polynômes du numérateur et du dénominateur :

$\displaystyle\lim_{x \to -1}\frac{x^3+2x^2-x-2}{x^3+5x^2+7x+3}=\lim_{x \to -1}\frac{(x-1)(x+1)(x+2)}{(x+1)^2(x+3)}$

Maintenant, nous simplifions la fraction en éliminant les facteurs qui se répètent au numérateur et au dénominateur :

$\displaystyle\lim_{x \to -1} \cfrac{(x-1)\cancel{(x+1)}(x+2)}{(x+1)^{\cancel{2}}(x+3)}=\lim_{x \to -1}\cfrac{(x-1)(x+2)}{(x+1)(x+3)}$

Et on calcule à nouveau la limite :

$\displaystyle\lim_{x \to -1}\frac{(x-1)(x+2)}{(x+1)(x+3)}=\frac{(-1-1)(-1+2)}{(-1+1)(-1+3)}=\frac{-2\cdot 1}{0 \cdot 2}=\frac{-2}{0} =\infty$

Mais maintenant nous nous retrouvons avec l’indétermination d’un nombre divisé par 0. Il faut donc calculer les limites latérales de la fonction lorsque x tend vers -1.

Nous résolvons d’abord la limite latérale de la fonction au point x=-1 à gauche :

$\displaystyle\lim_{x \to -1^{-}}\frac{(x-1)(x+2)}{(x+1)(x+3)}=\frac{(-1-1)\cdot (-1+2)}{(-1+1)\cdot (-1+3)}=\frac{-2}{-0}=+\infty$

Et puis on calcule la limite latérale de la fonction au point x=-1 à droite :

$\displaystyle\lim_{x \to -1^{+}}\frac{(x-1)(x+2)}{(x+1)(x+3)}=\frac{(-1-1)\cdot (-1+2)}{(-1+1)\cdot (-1+3)}=\frac{-2}{+0}=-\infty$

Donc, puisque les deux limites latérales ne coïncident pas, la limite de la fonction en x=-1 n’existe pas :

$\displaystyle\displaystyle \lim_{x \to -1^-}f(x)= +\infty\neq\lim_{x \to -1^+}f(x)=-\infty\ \bm{\longrightarrow} \ \cancel{\exists} \lim_{x \to -1} f(x)$

Zéro indétermination entre zéro (0/0)

Comment résoudre l’indétermination zéro entre zéro (0/0)

Indétermination 0/0 avec racines

Exercices résolus sur l’indétermination 0/0

Exercice 1

Exercice 2

Exercice 3

Exercice 4

Exercice 5

Leave a Comment Cancel Reply