Vous trouverez ici ce que sont les fonctions polynomiales et quels sont tous les types de fonctions polynomiales. De plus, nous expliquons également les propriétés des fonctions polynomiales.
Qu’est-ce qu’une fonction polynomiale ?
Une fonction polynomiale est une fonction dont l’expression algébrique est un polynôme , c’est-à-dire qu’une fonction polynomiale est définie par l’addition ou la soustraction d’un nombre fini de termes de degré différent.
Par conséquent, une fonction polynomiale est décrite mathématiquement par l’expression suivante :
![]()
D’autre part, les fonctions polynomiales peuvent également être définies à l’aide de la formule suivante :
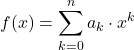
où les termes
![]() et
et![]() sont respectivement le coefficient et la variable de chaque monôme qui forme la fonction polynomiale.
sont respectivement le coefficient et la variable de chaque monôme qui forme la fonction polynomiale.
Le terme
![]() , appelé terme principal, indique le degré de la fonction polynomiale, puisqu’il s’agit du monôme de degré le plus élevé de la fonction. Autrement dit, le plus grand exposant de valeur est celui qui indique le degré de la fonction polynomiale.
, appelé terme principal, indique le degré de la fonction polynomiale, puisqu’il s’agit du monôme de degré le plus élevé de la fonction. Autrement dit, le plus grand exposant de valeur est celui qui indique le degré de la fonction polynomiale.
Bien que nous verrons plus de caractéristiques des fonctions polynomiales ci-dessous, le domaine de toute fonction polynomiale est tous les nombres réels.
Types de fonctions polynomiales
Compte tenu de la définition de fonction polynomiale, nous allons maintenant voir quels sont tous les types de fonctions polynomiales qui existent.
fonction constante
La fonction constante est une fonction polynomiale de degré 0, c’est donc un type de fonction qui prend toujours la même image pour toute valeur de la variable indépendante (x).
L’expression générale de la fonction constante est la suivante :
![]()
Par exemple, les trois fonctions suivantes sont des constantes ou des fonctions polynomiales de degré zéro :
![]()
La représentation graphique d’une fonction constante est une ligne horizontale (parallèle à l’axe des x) avec une valeur égale à la constante.

Vous pouvez voir plus de fonctionnalités sur ce type de fonction dans le lien suivant :
➤ Voir : caractéristiques de la fonction constante
Fonction linéaire
Une fonction linéaire , aussi appelée fonction affine, est une fonction polynomiale du premier degré. Ainsi une fonction polynomiale de ce type ne peut être composée que d’un terme linéaire et d’un terme indépendant :
![]()
Où
![]() est la pente de la droite et
est la pente de la droite et![]() est l’ordonnée à l’origine, c’est-à-dire là où la fonction croise l’axe Y.
est l’ordonnée à l’origine, c’est-à-dire là où la fonction croise l’axe Y.
Exemples de fonctions linéaires ou fonctions polynomiales du premier degré :
![]()
Certains distinguent la fonction linéaire de la fonction affine selon que la fonction a pour terme
![]() ou non, étant la fonction affine avec l’ordonnée à l’origine et la fonction linéaire sans.
ou non, étant la fonction affine avec l’ordonnée à l’origine et la fonction linéaire sans.
La représentation graphique des fonctions linéaires sont toujours des lignes dont le degré d’inclinaison dépend de la valeur de la pente de la fonction.
Ci-dessous vous pouvez voir graphiquement la fonction polynomiale du premier degré
![]()

Cependant, pour représenter graphiquement une fonction linéaire, vous devez être clair sur plusieurs concepts. Dans le lien suivant, vous trouverez l’explication étape par étape de la façon de représenter graphiquement une fonction polynomiale de ce type :
➤ Voir : Représentation graphique d’une fonction linéaire
Fonction quadratique
Une fonction quadratique est une fonction polynomiale de degré 2, c’est-à-dire une fonction dont le terme de degré supérieur est de second degré.
Par conséquent, la formule d’une fonction quadratique est la suivante :
![]()
Où
![]() est le terme quadratique,
est le terme quadratique,![]() le terme linéaire et
le terme linéaire et![]() le terme indépendant de la fonction polynomiale.
le terme indépendant de la fonction polynomiale.
Exemples de fonctions quadratiques ou de fonctions polynomiales du second degré :
![]()
Le graphique d’une fonction quadratique est toujours une parabole et sa forme dépend du signe du coefficient directeur.
![]()
- Si le coefficient
 est positif, la fonction quadratique est convexe (en forme de
est positif, la fonction quadratique est convexe (en forme de ).
). - Au lieu de cela, si le coefficient
 est négatif, la fonction quadratique est concave (en forme de
est négatif, la fonction quadratique est concave (en forme de ).
).


Ainsi, avec le signe du coefficient principal de la fonction polynomiale du second degré, nous pouvons connaître la forme que prendra son graphique, mais pour en faire sa représentation graphique exacte, une procédure spécifique doit être suivie. Vous pouvez voir cette procédure dans le lien suivant :
➤ Voir : Représentation graphique d’une fonction quadratique
fonction cubique
Une fonction cubique est une fonction polynomiale du troisième degré. Par conséquent, ce type de fonctions polynomiales s’exprime algébriquement comme suit :
![]()
Exemples de fonctions cubiques ou de fonctions polynomiales du troisième degré :
![]()
![]()
Les représentations graphiques des fonctions cubiques correspondent à des courbes cubiques. Cependant, pour représenter ce type de fonctions dans un graphe, une procédure compliquée doit être suivie (elle inclut les dérivées). Vous pouvez voir comment c’est fait ici :
➤ Voir : Comment représenter une fonction
Comme vous pouvez le voir, les types de fonctions polynomiales sont en fait infinis, puisqu’un polynôme peut avoir des termes infinis. Ainsi, par exemple, une fonction quartique est comme une fonction cubique mais avec l’ajout d’un terme quadratique. L’important est que vous compreniez que le type de fonction polynomiale est marqué par le degré de la fonction.
Propriétés des fonctions polynomiales
Les fonctions polynomiales ont les caractéristiques suivantes :
- Le domaine de toute fonction polynomiale est l’ensemble des nombres réels.
![]()
- Toutes les fonctions polynomiales sont continues.
- Les fonctions polynomiales de degré supérieur à 1 n’ont pas d’asymptotes.
- Quel que soit le type de fonction polynomiale dont il s’agit, le seul point d’intersection avec l’axe des ordonnées (axe Y) est à la hauteur de son terme indépendant, c’est-à-dire au point suivant :
![]()
- Par contre, une fonction polynomiale intercepte l’axe des abscisses (axe X), au plus, autant de fois que le degré de la fonction.
- Si une fonction polynomiale n’a que des termes de degré pair, cela implique qu’elle est symétrique par rapport à l’axe OY. D’autre part, si une fonction polynomiale n’a que des termes de degré impair, cela signifie que la fonction est symétrique par rapport à l’origine des coordonnées.
- Le nombre d’extrema relatifs (maximum ou minimum) d’une fonction polynomiale est, au plus, le degré du polynôme de la fonction moins 1.
- Le nombre de points d’inflexion d’une fonction polynomiale est au plus égal au degré du polynôme de la fonction moins 2.
- Les opérations peuvent être effectuées avec des fonctions polynomiales :
- La somme de deux fonctions polynomiales donne une autre fonction polynomiale.
- Le produit de deux fonctions polynomiales donne naissance à une autre fonction polynomiale.
- La multiplication d’une fonction polynomiale par un scalaire (nombre réel) donne une fonction polynomiale similaire mais avec son graphique réduit ou développé.
- La composition de deux fonctions polynomiales est égale à une autre fonction polynomiale.