Dans cet article, nous verrons comment représenter tout type de fonction sur un graphique. De plus, vous trouverez des exercices résolus étape par étape sur la représentation de fonctions sur un graphique.
Comment représenter une fonction sur un graphique
Pour représenter une fonction sur un graphique, les étapes suivantes doivent être effectuées :
- Trouvez le domaine de la fonction.
- Calculez les points de coupure de la fonction avec les axes cartésiens.
- Calculez les asymptotes de la fonction.
- Étudiez la monotonie de la fonction et trouvez ses extrêmes relatifs .
- Étudiez la courbure de la fonction et trouvez ses points d’inflexion .
- Tracez les points de coupure, les asymptotes, les extrema relatifs et les points d’inflexion, puis tracez la fonction.
Exemple de représentation d’une fonction
Afin que vous puissiez voir comment une fonction est représentée graphiquement, nous allons résoudre l’exercice suivant étape par étape :
- Représentez la fonction rationnelle suivante sur un graphique :
![]()
La première chose à faire est de calculer le domaine de la fonction . C’est une fonction rationnelle, nous devons donc mettre le dénominateur égal à zéro pour voir quels nombres n’appartiennent pas au domaine de la fonction :
![]()
![]()
Ainsi, lorsque x vaut 1, le dénominateur sera 0 et, par conséquent, la fonction n’existera pas. Le domaine de la fonction est donc constitué de tous les nombres réels sauf x=1.
![]()
Pour trouver le point d’intersection avec l’axe X , il faut résoudre l’équation
![]() Puisque la fonction a toujours une valeur de 0 sur l’axe X :
Puisque la fonction a toujours une valeur de 0 sur l’axe X :
![]()
![]()
Le terme
![]() Il s’agit de diviser tout le côté gauche, nous pouvons donc le multiplier par tout le côté droit :
Il s’agit de diviser tout le côté gauche, nous pouvons donc le multiplier par tout le côté droit :
![]()
![]()
![]()
Le point d’intersection avec l’axe OX est donc :
![]()
Et pour trouver le point d’intersection avec l’axe Y , on calcule
![]() Parce que x est toujours égal à 0 sur l’axe Y :
Parce que x est toujours égal à 0 sur l’axe Y :
![]()
Par conséquent, le point de coupure avec l’axe OY est :
![]()
Dans ce cas, lorsque la fonction passe par l’origine des coordonnées, le point d’intersection avec l’axe X coïncide avec le point d’intersection avec l’axe Y.
Une fois que nous connaissons le domaine et les points de coupure, nous devons calculer les asymptotes de la fonction .
Pour voir si la fonction a des asymptotes verticales, nous devons calculer la limite de la fonction en des points qui n’appartiennent pas au domaine (dans ce cas x=1). Et si le résultat est infini, c’est une asymptote verticale. Pourtant:
![]()
Puisque la limite de la fonction lorsque x tend vers 1 donne l’infini, x=1 est une asymptote verticale :
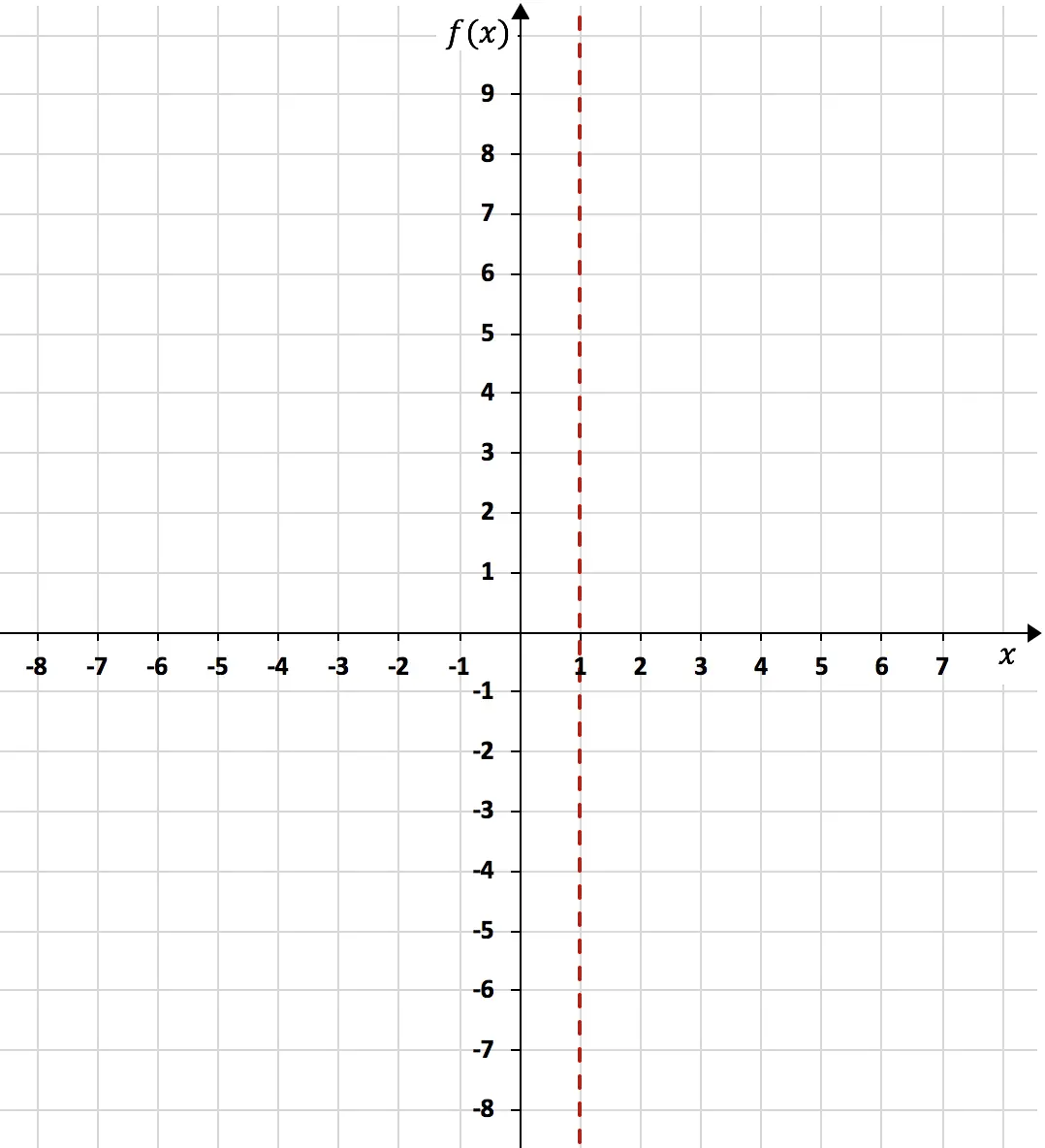
Une fois l’asymptote verticale calculée, il faut calculer les limites latérales de la fonction par rapport à elle. Puisque nous ne savons pas si la fonction tendra vers -∞ ou +∞ lorsqu’elle s’approche de x=1 par la gauche, et nous ne savons pas quand elle s’approche de x=1 par la droite.
Ainsi, nous procédons au calcul de la limite latérale gauche de la fonction à x=1 :
![]()
Pour calculer numériquement une limite latérale en un point, nous devons substituer un nombre dans la fonction qui est très proche du point. Dans ce cas, nous voulons un nombre très proche de 1 à gauche, comme 0,9. On substitue donc le point 0.9 dans la fonction :
![]()
Les limites latérales à une asymptote ne peuvent donner que +∞ ou -∞. Et comme en substituant dans la fonction un nombre très proche de 1 à gauche on a obtenu un résultat négatif, la limite à gauche est -∞ :
![]()
Maintenant, nous faisons la même procédure avec la limite latérale à droite :
![]()
Nous substituons dans la fonction un nombre très proche de 1 à droite. Par exemple le point 1.1 :
![]()
Dans ce cas, le résultat de la limite latérale est un nombre positif. La limite à droite est donc +∞ :
![]()
En conclusion, à x=1 la fonction tend vers moins l’infini à gauche, et plus l’infini à droite :
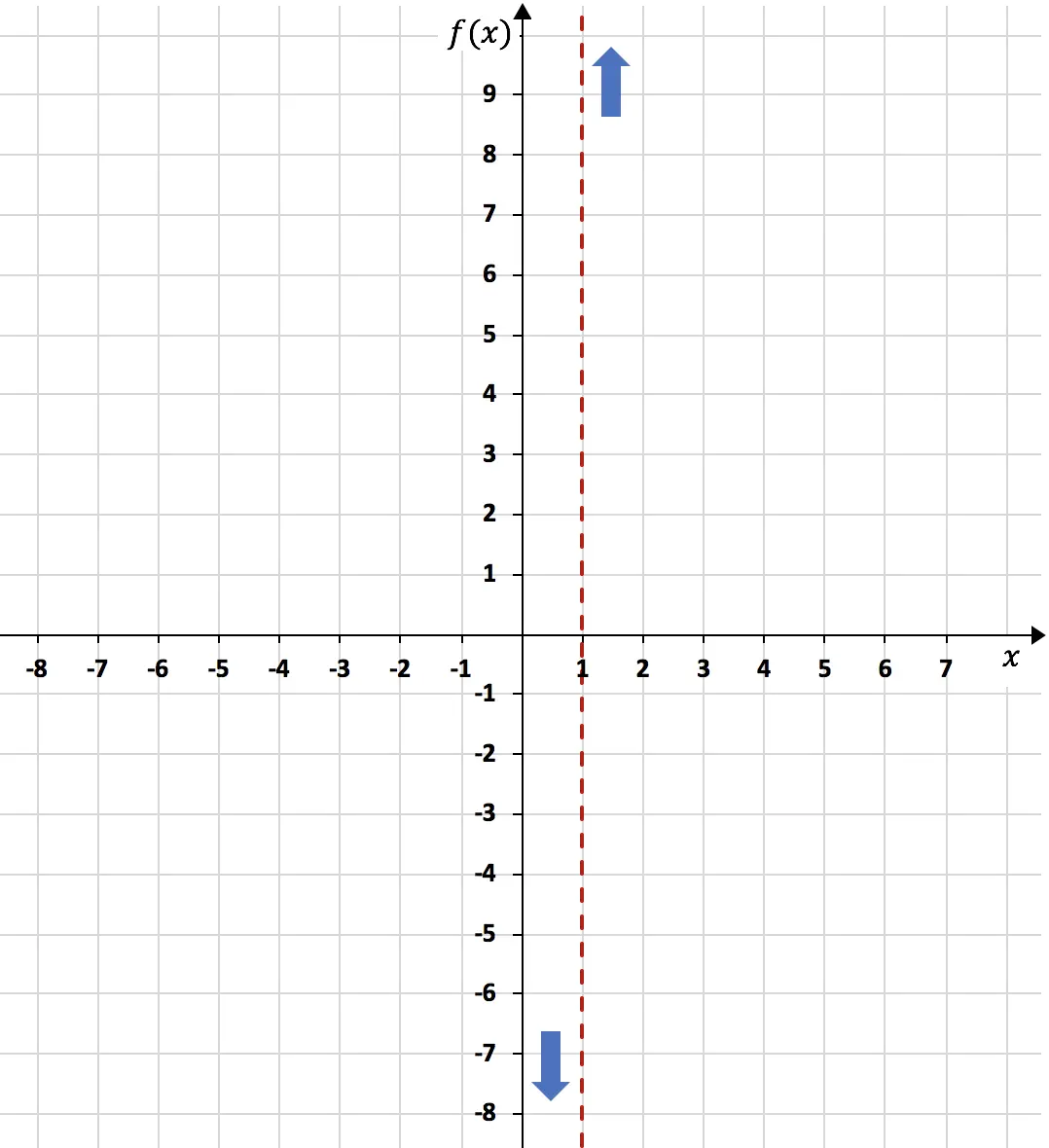
En revanche, l’asymptote horizontale de la fonction sera le résultat de la limite infinie de la fonction. Pourtant:
![]()
Rappelez-vous comment calculer les limites infinies des fonctions rationnelles :
![Rendered by QuickLaTeX.com \displaystyle \lim_{x \to \pm \infty}}\frac{a_nx^r+a_{n-1}x^{r-1}+a_{n-2}x^{r-2}+\dots}{b_nx^s+b_{n-1}x^{s-1}+b_{n-2}x^{s-2}+\dots}=\left\{ \begin{array}{lcl} 0 & \text{si} & r<s \\[3ex]="" \cfrac{a_n}{b_n}="" &="" \text{si}="" r="s" \\[5ex]="" \pm="" \infty="">s \end{array}\right.](https://mathority.org/wp-content/ql-cache/quicklatex.com-2c969e4b99985b44006e57d554ff0247_l3.png)
La limite infinie de la fonction nous a donné +∞, donc la fonction n’a pas d’asymptote horizontale.
Nous calculons maintenant l’asymptote oblique. Les asymptotes obliques sont de la forme
![]() . ET
. ET![]() Il est calculé avec la formule suivante :
Il est calculé avec la formule suivante :
![]()
![]()
Le x est comme s’il avait un 1 comme dénominateur :
![]()
C’est une division de fractions, donc on les multiplie transversalement :
![]()
![]()
Et on calcule la limite :
![]()
Donc m=1. Maintenant on calcule
![]() avec la formule suivante :
avec la formule suivante :
![]()
![Rendered by QuickLaTeX.com \displaystyle n = \lim_{x \to +\infty} \left[\cfrac{x^2}{x-1}-1x\right] = \cfrac{+\infty}{+\infty} -(+\infty) = +\infty - \infty](https://mathority.org/wp-content/ql-cache/quicklatex.com-10dfa8fdcfbf0c978e02374654a66b7d_l3.png)
Mais on obtient l’indétermination infini moins l’infini, il faut donc réduire les termes à un dénominateur commun. Pour ce faire, on multiplie et divise le terme x par le dénominateur de la fraction :
![Rendered by QuickLaTeX.com \displaystyle n = \lim_{x \to +\infty}\left[\cfrac{x^2}{x-1}-x\right] = \lim_{x \to +\infty} \left[\cfrac{x^2}{x-1}-\cfrac{x\cdot (x-1)}{x-1} \right] = \lim_{x \to +\infty} \left[\cfrac{x^2}{x-1}-\cfrac{x^2-x}{x-1}\right]](https://mathority.org/wp-content/ql-cache/quicklatex.com-70026c2aed1bb58a120f8c18423d9ef5_l3.png)
Maintenant que les deux termes ont le même dénominateur, on peut les regrouper :
![Rendered by QuickLaTeX.com \displaystyle n = \lim_{x \to +\infty} \left[\cfrac{x^2-(x^2-x)}{x-1} \right] =\lim_{x \to +\infty} \left[\cfrac{x}{x-1} \right]](https://mathority.org/wp-content/ql-cache/quicklatex.com-7702287a02af6d8e3dddaa3f0c6eb1b5_l3.png)
Et enfin nous résolvons la limite :
![Rendered by QuickLaTeX.com \displaystyle n =\lim_{x \to +\infty} \left[\cfrac{x}{x-1} \right] = \cfrac{+\infty}{+\infty} = \cfrac{1}{1} = 1](https://mathority.org/wp-content/ql-cache/quicklatex.com-feb5faa9dc5d3b68d3273ad4d75d2bb1_l3.png)
Donc n = 1. L’asymptote oblique est donc :
![]()
![]()
![]()
Une fois que l’on a calculé l’asymptote oblique, on la représente sur le même graphique en faisant un tableau de valeurs :
![]()

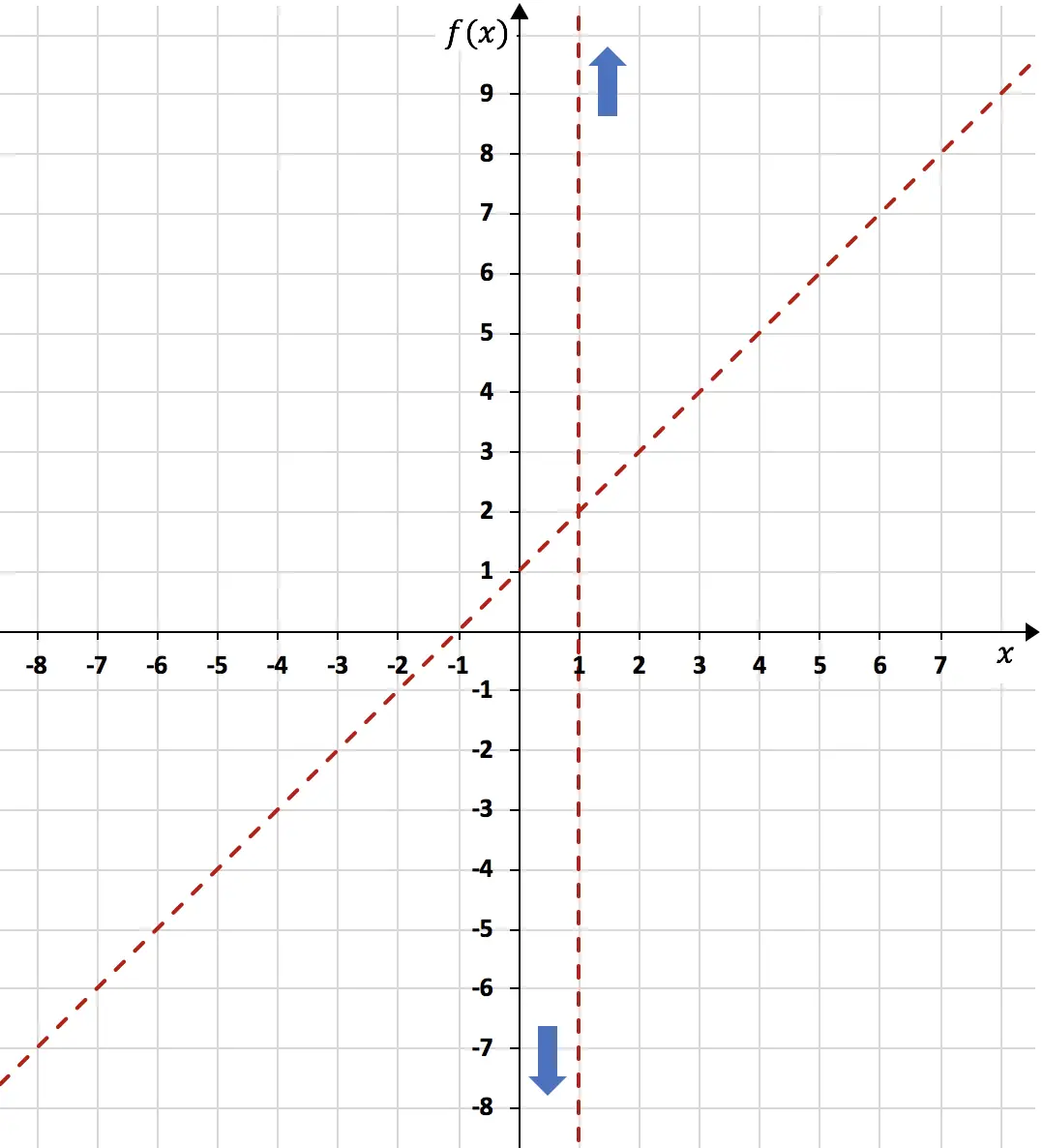
Maintenant que nous connaissons toutes les asymptotes de la fonction, nous devons analyser la monotonie de la fonction . Autrement dit, nous devons étudier dans quels intervalles la fonction augmente et dans quels intervalles elle diminue. On calcule donc la dérivée première de la fonction :
![]()
![]()
Et maintenant, nous fixons la dérivée égale à 0 et résolvons l’équation :
![]()
![]()
Le terme
![]() Il s’agit de diviser tout le côté gauche, nous pouvons donc le multiplier par tout le côté droit :
Il s’agit de diviser tout le côté gauche, nous pouvons donc le multiplier par tout le côté droit :
![]()
![]()
Nous extrayons le facteur commun pour résoudre l’équation quadratique :
![]()
Pour que la multiplication soit égale à 0, il faut qu’un des deux éléments de la multiplication soit nul. Par conséquent, nous fixons chaque facteur égal à 0 et obtenons les deux solutions de l’équation :
![Rendered by QuickLaTeX.com \displaystyle x\cdot(x-2) =0 \longrightarrow \begin{cases} \bm{x=0} \\[2ex] x-2=0 \ \longrightarrow \ \bm{x= 2} \end{cases}](https://mathority.org/wp-content/ql-cache/quicklatex.com-55127e675ce8f7742db17d565c2ae507_l3.png)
Nous représentons maintenant sur la droite numérique tous les points critiques trouvés, c’est-à-dire les points qui n’appartiennent pas au domaine (x=1) et ceux qui annulent la dérivée (x=0 et x=2) :

Et on évalue le signe de la dérivée dans chaque intervalle, pour savoir si la fonction augmente ou diminue. Nous prenons donc un point dans chaque intervalle (jamais les points critiques) et regardons quel signe la dérivée a à ce point :
![]()
![]()
![]()
![]()
![]()
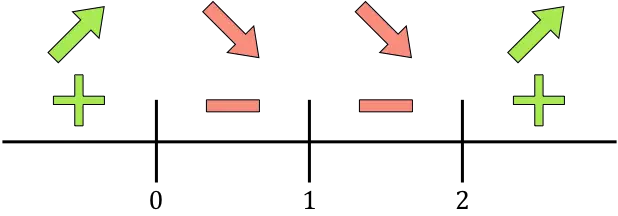
Si la dérivée est positive, cela signifie que la fonction augmente, et si la dérivée est négative, cela signifie que la fonction diminue. Par conséquent, les intervalles de croissance et de diminution sont :
Croissance:
![]()
Diminuer:
![]()
De plus, à x=0 la fonction passe de croissante à décroissante, donc x=0 est un maximum relatif de la fonction. Et à x=2, la fonction passe de décroissante à croissante, donc x=2 est un minimum relatif de la fonction.
Enfin, nous substituons les extrêmes trouvés dans la fonction d’origine pour trouver la coordonnée Y des points :
![]()
![]()
Les extrêmes relatifs de la fonction sont donc :
Maximum sur le point
![]()
Minimum au point
![]()
Nous représentons le maximum et le minimum sur le graphique :
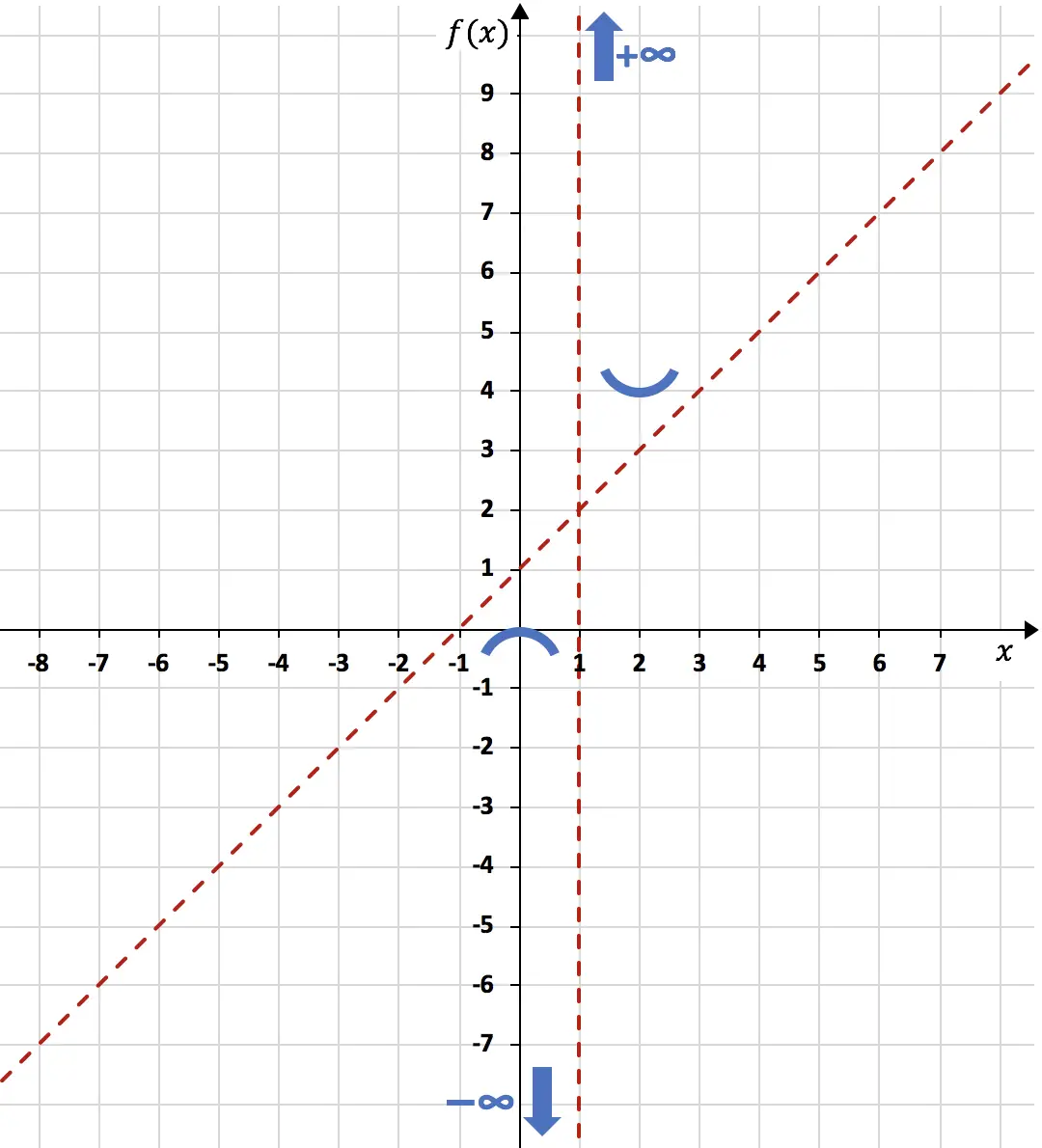
Enfin, il suffit d’ étudier la courbure de la fonction , c’est-à-dire d’étudier les intervalles de concavité et de convexité de la fonction. Pour ce faire, on calcule sa dérivée seconde :
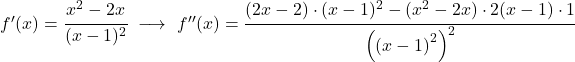
![]()
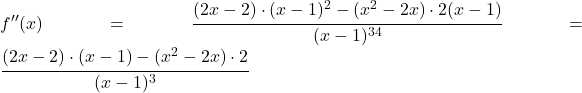
![]()
![]()
Et maintenant, nous fixons la dérivée seconde égale à zéro et résolvons l’équation :
![]()
![]()
![]()
![]()
2 ne sera jamais égal à 0, donc l’équation
![]() Il n’y a pas de solution.
Il n’y a pas de solution.
Nous représentons maintenant sur la droite numérique tous les points critiques trouvés, c’est-à-dire les points qui n’appartiennent pas au domaine (x=1) et ceux qui annulent la dérivée seconde (dans ce cas il n’y en a pas) :
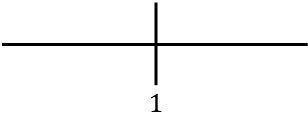
Et on évalue le signe de la dérivée dans chaque intervalle, pour savoir si la fonction est convexe ou concave. Nous prenons donc un point dans chaque intervalle (jamais les points singuliers) et regardons quel signe la dérivée a à ce point :
![]()
![]()
![]()

Et enfin on en déduit les intervalles de concavité et de convexité de la fonction. Si la dérivée seconde est positive, cela signifie que la fonction est convexe.
![]() , et si la dérivée seconde est négative cela signifie que la fonction est concave
, et si la dérivée seconde est négative cela signifie que la fonction est concave![]() . Les intervalles de concavité et de convexité sont donc :
. Les intervalles de concavité et de convexité sont donc :
Convexe
![]() :
:![]()
Concave
![]() :
:![]()
Cependant, même s’il y a un changement de courbure à x=1, il ne s’agit pas d’un point d’inflexion. Parce que x=1 n’appartient pas au domaine de la fonction.
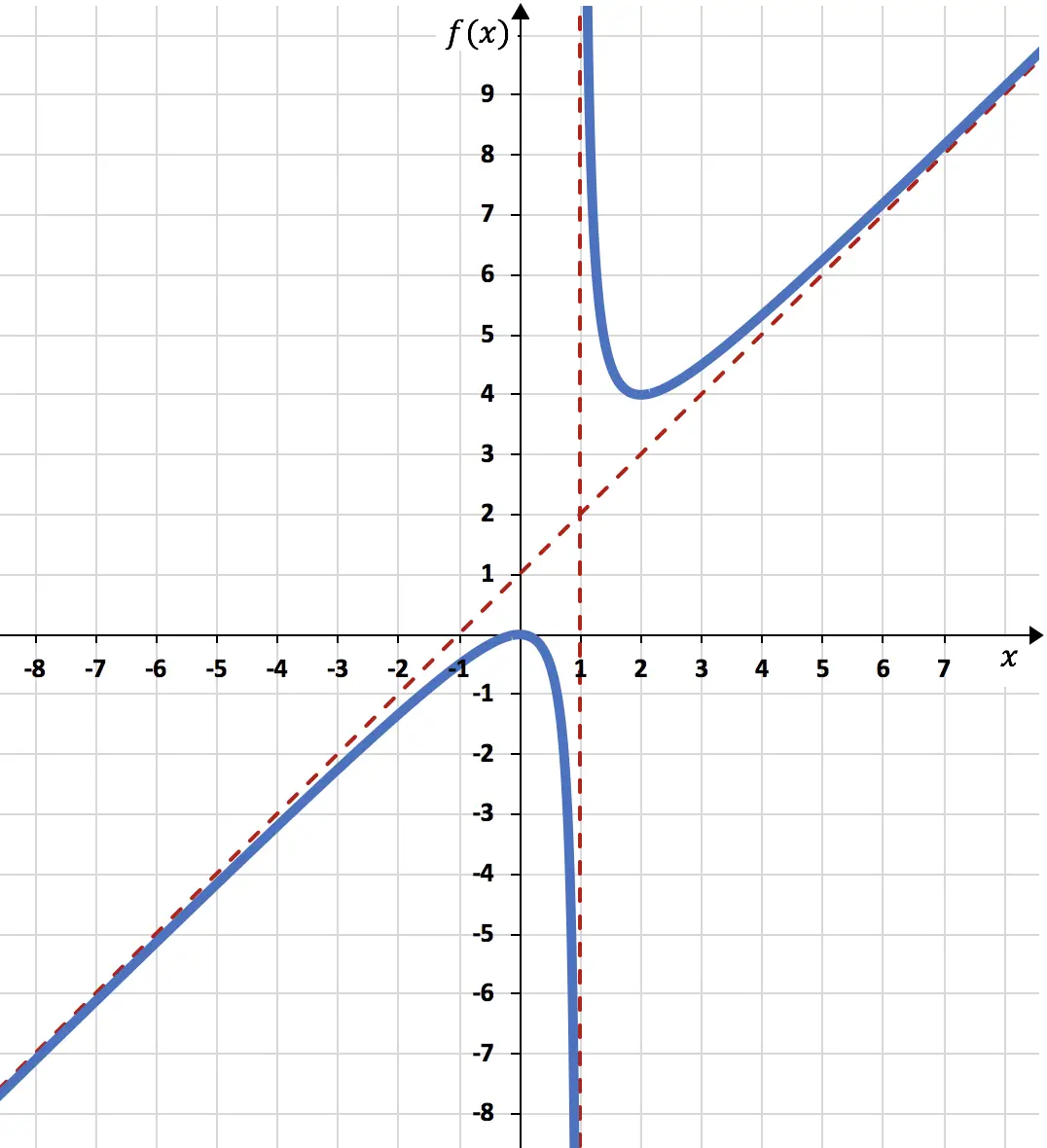
Nous pouvons donc finir de représenter la fonction à l’aide de tout ce que nous avons calculé :
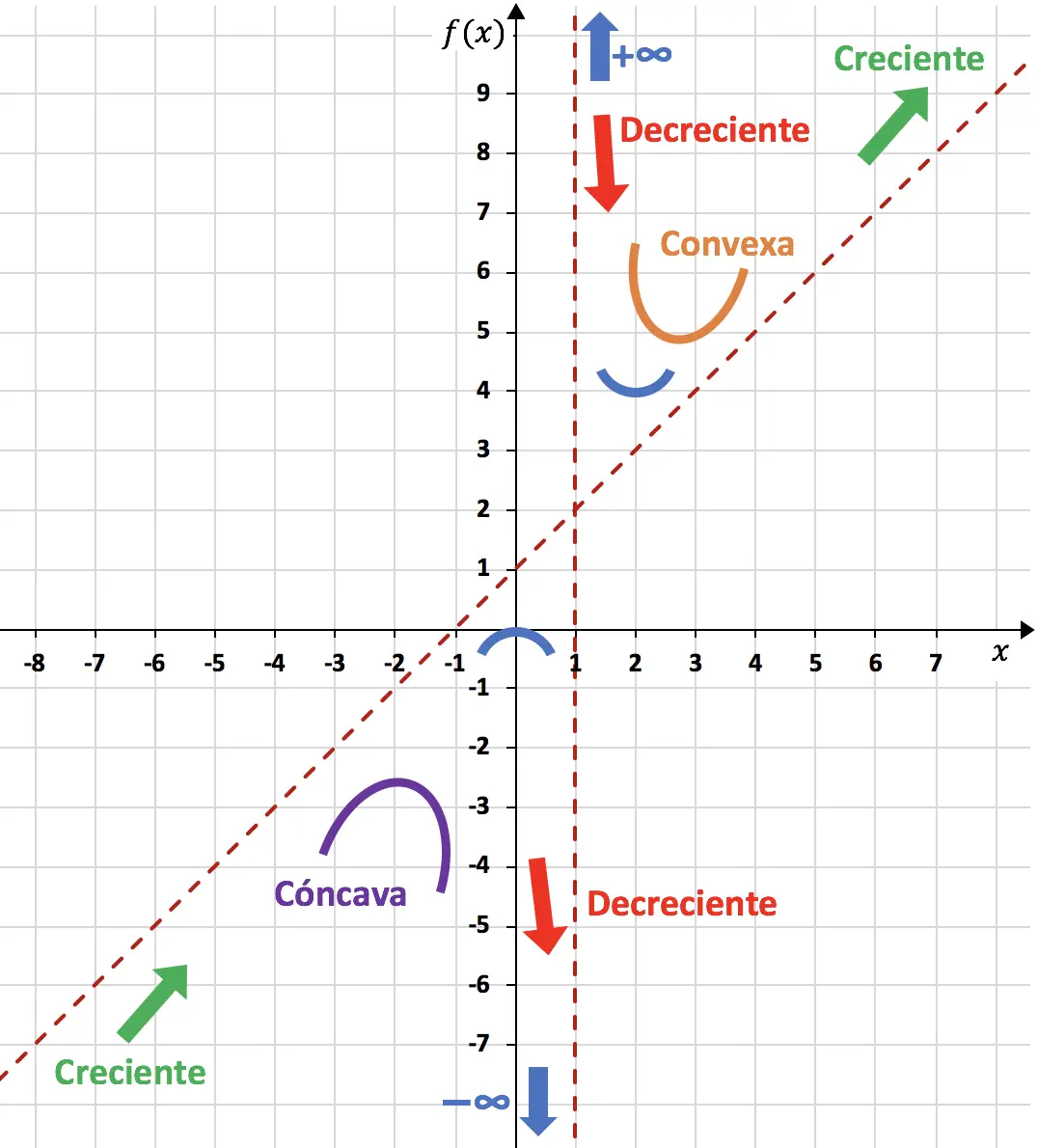
La fonction représentée sur le graphique ressemble donc à ceci :
Exercices résolus pour représenter des fonctions
Exercice 1
Représentez la fonction polynomiale suivante sur un graphique :
![]()
La première chose à faire est de calculer le domaine de définition de la fonction. Il s’agit d’une fonction polynomiale, donc le domaine est composé uniquement de nombres réels :
![]()
Pour trouver le point d’intersection avec l’axe X, on résout
![]()
![]()
![]()
Il s’agit d’une équation de degré supérieur à 2. Par conséquent, nous factorisons l’équation :
![]()
Donc x=-1 est une solution. Et on calcule les autres solutions en résolvant l’équation quadratique résultante :
![Rendered by QuickLaTeX.com \begin{aligned}x & =\cfrac{-b \pm \sqrt{b^2-4ac}}{2a} =\cfrac{-(-4) \pm \sqrt{(-4)^2-4\cdot 1 \cdot 4}}{2\cdot 1} \\[2ex] &=\cfrac{+4 \pm \sqrt{16-16}}{2} =\cfrac{4 \pm \sqrt{0}}{2} = \cfrac{4 }{2 } = 2\end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-e79a2a2f6650c4095c0dca52188c40c3_l3.png)
Les points d’intersection avec l’axe X sont donc :
![]() et
et![]()
Et pour trouver le point d’intersection avec l’axe Y, on calcule
![]() Puisque x est toujours égal à 0 sur l’axe Y :
Puisque x est toujours égal à 0 sur l’axe Y :
![]()
Le point d’intersection avec l’axe Y est donc :
![]()
Pour voir si la fonction a des asymptotes verticales, nous devons calculer la limite de la fonction en des points qui n’appartiennent pas au domaine. Dans ce cas, le domaine inclut tous les nombres réels. La fonction n’a donc pas d’asymptote verticale.
En revanche, l’asymptote horizontale de la fonction sera le résultat de la limite infinie de la fonction. Pourtant:
![]()
La limite infinie de la fonction nous a donné +∞, donc la fonction n’a pas d’asymptote horizontale.
Nous calculons maintenant l’asymptote oblique. Les asymptotes obliques sont de la forme
![]() ET
ET![]() Il est calculé avec la formule suivante :
Il est calculé avec la formule suivante :
![]()
![]()
La limite nous a donné +∞, donc la fonction n’a pas non plus d’asymptote oblique.
Pour étudier la monotonie de la fonction, il faut d’abord calculer sa dérivée :
![]()
Maintenant, nous fixons la dérivée égale à 0 et résolvons l’équation :
![]()
![]()
![]()
![Rendered by QuickLaTeX.com \displaystyle x\cdot(3x-6) =0 \longrightarrow \begin{cases} \bm{x=0} \\[2ex] 3x-6=0 \ \longrightarrow \ x= \cfrac{6}{3} = 2 \end{cases}](https://mathority.org/wp-content/ql-cache/quicklatex.com-d23e2b378508baca9f51117fc8767e90_l3.png)
Nous représentons maintenant sur la droite numérique tous les points singuliers obtenus, c’est-à-dire les points qui n’appartiennent pas au domaine (dans ce cas, ils appartiennent tous) et ceux qui annulent la dérivée (x=0 et x=2) :

Et on évalue le signe de la dérivée dans chaque intervalle, pour savoir si la fonction augmente ou diminue. Nous prenons donc un point dans chaque intervalle (jamais les points singuliers) et regardons quel signe la dérivée a à ce point :
![]()
![]()
![]()

Si la dérivée est positive, cela signifie que la fonction augmente, et si la dérivée est négative, cela signifie que la fonction diminue. Par conséquent, les intervalles de croissance et de diminution sont :
Croissance:
![]()
Diminuer:
![]()
La fonction passe de croissante à décroissante à x=0, donc x=0 est un maximum de la fonction. Et la fonction passe de décroissante à croissante à x=2, donc x=2 est un minimum de la fonction.
Enfin, nous substituons les extrêmes trouvés dans la fonction d’origine pour trouver les coordonnées Y des points :
![]()
![]()
Les extrêmes relatifs de la fonction sont donc :
Maximum sur le point
![]()
Minimum au point
![]()
Pour étudier la courbure de la fonction, on calcule sa dérivée seconde :
![]()
Maintenant, nous fixons la dérivée seconde égale à 0 et résolvons l’équation :
![]()
![]()
![]()
![]()
On représente sur la ligne tous les points singuliers trouvés, c’est-à-dire les points qui n’appartiennent pas au domaine (dans ce cas ils appartiennent tous) et ceux qui annulent la dérivée (x=1) :

Et maintenant nous évaluons le signe de la dérivée seconde dans chaque intervalle, pour savoir si la fonction est concave ou convexe. Nous prenons donc un point dans chaque intervalle (jamais les points singuliers) et regardons quel signe la dérivée seconde a à ce point :
![]()
![]()

Si la dérivée seconde est positive, cela signifie que la fonction est convexe.
![]() , et si la dérivée seconde est négative cela signifie que la fonction est concave
, et si la dérivée seconde est négative cela signifie que la fonction est concave![]() . Les intervalles de concavité et de convexité sont donc :
. Les intervalles de concavité et de convexité sont donc :
Convexe
![]() :
:![]()
Concave
![]() :
:![]()
De plus, la fonction passe de concave à convexe en x=1, donc x=1 est un point d’inflexion de la fonction.
Enfin, nous substituons les points d’inflexion trouvés dans la fonction d’origine pour trouver la coordonnée Y des points :
![]()
Les tournants de la fonction sont donc :
Points tournants :
![]()
Enfin, sur la base de toutes les informations que nous avons calculées, nous représentons graphiquement la fonction :
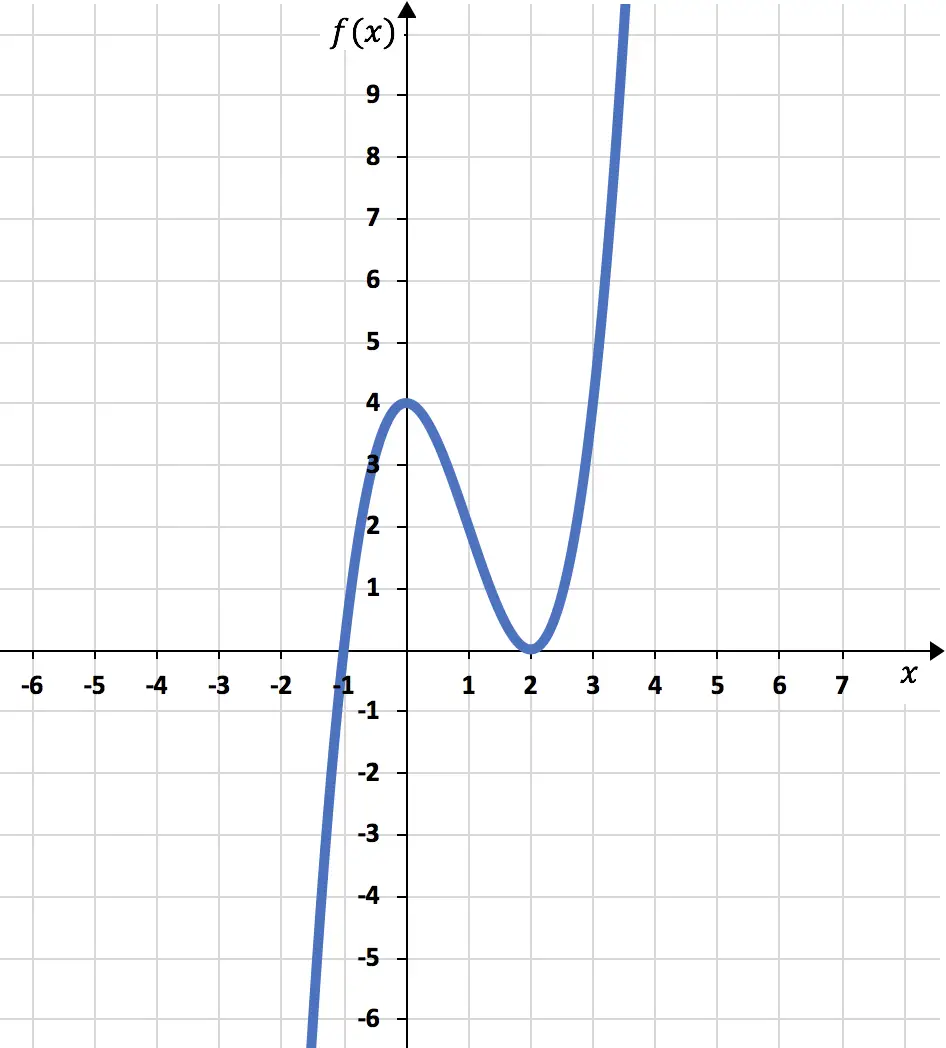
Exercice 2
Représentez graphiquement la fonction rationnelle suivante :
![]()
Pour trouver le domaine de la fonction, nous fixons le dénominateur égal. ramener la fraction à zéro et résoudre l’équation résultante :
![]()
![]()
![]()
![]()
![]()
Deuxièmement, nous déterminons les seuils de la fonction avec l’axe des abscisses égal à l’expression algébrique de la fonction. acier:
![]()
![]()
![]()
![]()
![]()
![]()
Il n’existe pas de racine carrée d’un nombre négatif. Par conséquent, la fonction ne coupe pas l’axe X.
Et pour trouver le point d’intersection avec l’axe des ordonnées, on évalue la fonction à x=0.
![]()
Le point d’intersection avec l’axe Y est donc :
![]()
Pour voir si la fonction a des asymptotes verticales, nous devons calculer la limite de la fonction en des points qui n’appartiennent pas au domaine (dans ce cas x=-1 et x=+1). Et si le résultat est infini, c’est une asymptote verticale. Pourtant:
![]()
Puisque la limite de la fonction lorsque x s’approche de -1 donne l’infini, x=-1 est une asymptote verticale.
On calcule les limites latérales de l’asymptote x=-1 en substituant dans la fonction un nombre qui en est très proche :
![]()
![]()
Voyons maintenant si x=+1 est une asymptote verticale :
![]()
Puisque la limite de la fonction lorsque x s’approche de +1 donne l’infini, x=+1 est une asymptote verticale.
On calcule les limites latérales de l’asymptote x=1 en substituant un nombre qui en est très proche dans la fonction :
![]()
![]()
En revanche, l’asymptote horizontale de la fonction sera le résultat de la limite infinie de la fonction. Pourtant:
![]()
La limite infinie de la fonction nous a donné 1, donc la fonction a une asymptote horizontale en y=1.
Puisque la fonction a une asymptote horizontale, elle n’aura pas d’asymptote oblique.
Nous dérivons la fonction puis étudions les intervalles de croissance et de diminution :
![]()
![]()
Maintenant, nous fixons la dérivée égale à 0 et résolvons l’équation :
![]()
![]()
![]()
![]()
![]()
On représente sur la ligne tous les points critiques calculés, qui sont les points qui n’appartiennent pas au domaine (x=-1 et x=+1) et ceux qui annulent la dérivée (x=0) :

Et on évalue le signe de la dérivée dans chaque intervalle, pour savoir si la fonction augmente ou diminue. Nous prenons donc un point dans chaque intervalle (jamais les points singuliers) et regardons quel signe la dérivée a à ce point :
![]()
![]()
![]()
![]()
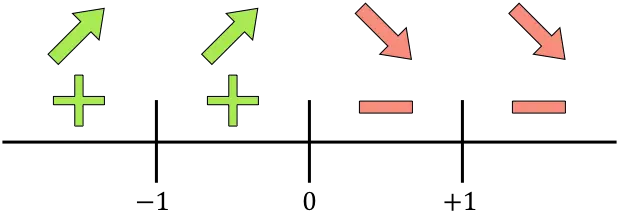
La fonction augmente là où la dérivée est positive et la fonction diminue là où la fonction est négative :
Croissance:
![]()
Diminuer:
![]()
La fonction passe de croissante à décroissante à x=0, donc x=0 est un maximum local de la fonction.
Nous substituons l’extremum trouvé dans la fonction d’origine pour trouver la coordonnée Y du point :
![]()
Les extrêmes relatifs de la fonction sont donc :
Maximum sur le point
![]()
Pour étudier la courbure de la fonction, on calcule sa dérivée seconde :
![Rendered by QuickLaTeX.com f'(x)=\cfrac{-6x}{\left(x^2-1 \right)^2} \ \longrightarrow <span class="ql-right-eqno"> </span><span class="ql-left-eqno"> </span><img src="https://mathority.org/wp-content/ql-cache/quicklatex.com-273969cf60ee8cf3413ee2f8b1db7688_l3.png" height="129" width="476" class="ql-img-displayed-equation quicklatex-auto-format" alt="\[f''(x)= \cfrac{-6 \cdot \left(x^2-1 \right)^2 - (-6x) \cdot 2(x^2-1) \cdot 2x}{ \left(\left(x^2-1 \right)^2\right)^2}$$ f''(x)= \cfrac{-6 \left(x^2-1 \right)^2 -(-6x)\cdot 4x(x^2-1)}{\left(x^2 -1\right)^4} =\]" title="Rendered by QuickLaTeX.com"/> \cfrac{-6 \left(x^2-1 \right)^2 + 24x^2(x^2-1)}{\left(x^2 -1\right)^4}](https://mathority.org/wp-content/ql-cache/quicklatex.com-802852beb818dd5a0dce2f30374f3a88_l3.png)
Tous les termes ont
![]() , on peut donc simplifier la fraction :
, on peut donc simplifier la fraction :
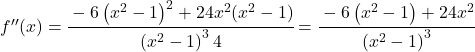
![]()
Maintenant, nous fixons la dérivée seconde égale à 0 et résolvons l’équation :
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Il n’existe pas de racine carrée d’un nombre négatif. Il n’y a donc aucun point qui corresponde
![]()
Maintenant nous représentons sur la ligne tous les points singuliers trouvés, c’est-à-dire les points qui n’appartiennent pas au domaine (x=-1 et x=+1) et ceux qui annulent la dérivée seconde (dans ce cas il n’y en a pas) :
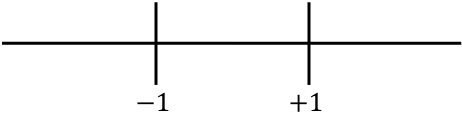
Et on évalue le signe de la dérivée seconde dans chaque intervalle, pour savoir si la fonction est concave ou convexe. Nous prenons donc un point dans chaque intervalle (jamais les points singuliers) et regardons quel signe la dérivée seconde a à ce point :
![]()
![]()
![]()

Si la dérivée seconde est positive, cela signifie que la fonction est convexe.
![]() , et si la dérivée seconde est négative cela signifie que la fonction est concave
, et si la dérivée seconde est négative cela signifie que la fonction est concave![]() . Les intervalles de concavité et de convexité sont donc :
. Les intervalles de concavité et de convexité sont donc :
Convexe
![]() :
:![]()
Concave
![]() :
:![]()
Cependant, bien qu’il y ait un changement de courbure à x=-1 et à x=1, ce ne sont pas des points d’inflexion. Parce qu’ils n’appartiennent pas au domaine de la fonction.
Et enfin, nous représentons graphiquement la fonction en utilisant tous les calculs effectués :
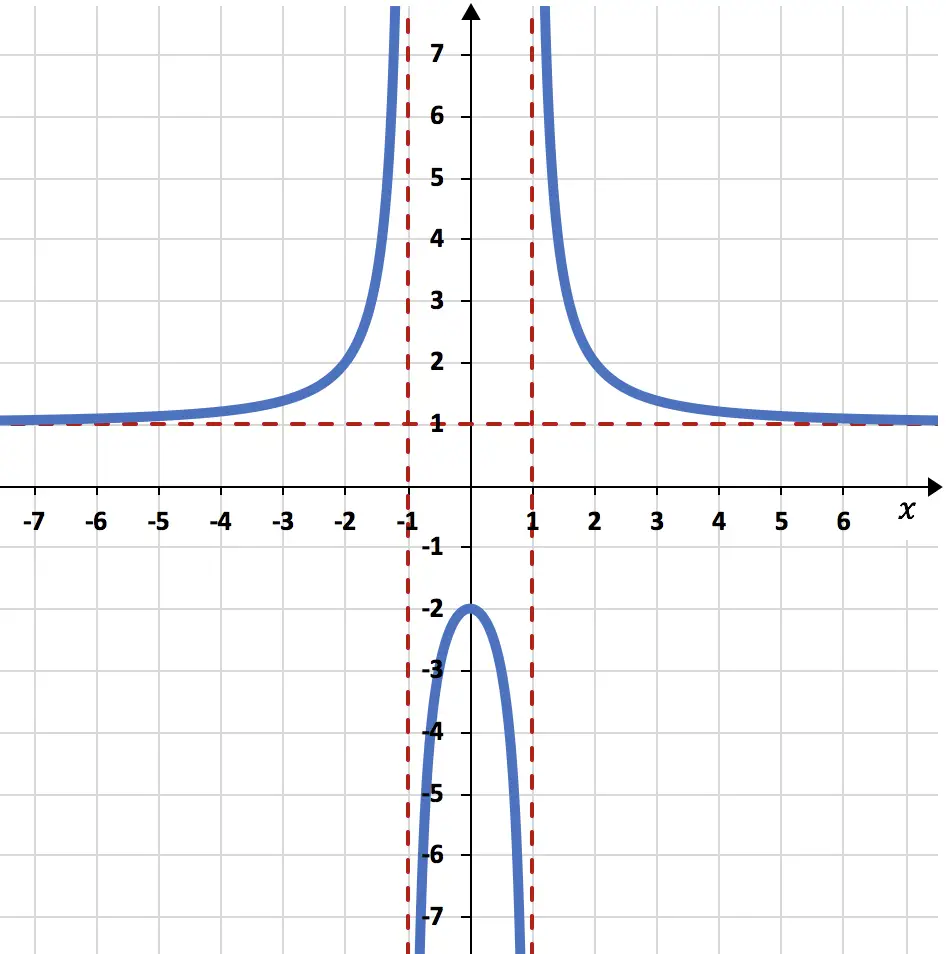
Exercice 3
Représentez la fonction rationnelle suivante sur un graphique :
![]()
C’est une fonction rationnelle, nous devons donc mettre le dénominateur égal à 0 pour voir quels nombres n’appartiennent pas au domaine de la fonction :
![]()
![]()
![]()
![]()
![]()
Pour trouver le point d’intersection avec l’axe X, on résout
![]() Puisque la fonction a toujours une valeur de 0 sur l’axe X :
Puisque la fonction a toujours une valeur de 0 sur l’axe X :
![]()
![]()
![]()
![]()
![]()
Le point d’intersection avec l’axe X est donc :
![]()
Et pour trouver le point d’intersection avec l’axe Y, on calcule
![]() Puisque x est toujours égal à 0 sur l’axe Y :
Puisque x est toujours égal à 0 sur l’axe Y :
![]()
Le point d’intersection avec l’axe Y est donc :
![]()
Dans ce cas, le point d’intersection avec l’axe X coïncide avec le point d’intersection avec l’axe Y, puisque la fonction passe par l’origine des coordonnées.
Pour voir si la fonction a des asymptotes verticales, nous devons calculer la limite de la fonction en des points qui n’appartiennent pas au domaine (dans ce cas x=-2 et x=+2). Et si le résultat est infini, c’est une asymptote verticale. Pourtant:
![]()
Puisque la limite de la fonction lorsque x tend vers -2 donne l’infini, x=-2 est une asymptote verticale.
On calcule les limites latérales de l’asymptote x=-2 en substituant dans la fonction un nombre qui en est très proche :
![]()
![]()
Voyons maintenant si x=+2 est une asymptote verticale :
![]()
Puisque la limite de la fonction lorsque x s’approche de +2 donne l’infini, x=+2 est une asymptote verticale.
On calcule les limites latérales de l’asymptote x=2 en substituant un nombre qui en est très proche dans la fonction :
![]()
![]()
En revanche, l’asymptote horizontale de la fonction sera le résultat de la limite infinie de la fonction. Pourtant:
![]()
La limite infinie de la fonction nous a donné +∞, donc la fonction n’a pas d’asymptote horizontale.
Nous calculons maintenant l’asymptote oblique. Les asymptotes obliques sont de la forme
![]() ET
ET![]() Il est calculé avec la formule suivante :
Il est calculé avec la formule suivante :
![]()
![]()
![]()
Une fois que l’on connaît la pente de l’asymptote oblique, on détermine l’ordonnée à l’origine à l’aide de la formule suivante :
![Rendered by QuickLaTeX.com \displaystyle n = \lim_{x \to +\infty} \left[f(x)-mx\right] = \lim_{x \to +\infty} \left[ \cfrac{x^3}{x^2-4}-1x\right]](https://mathority.org/wp-content/ql-cache/quicklatex.com-de4326a40acf34b64a28c9da8250bf00_l3.png)
![Rendered by QuickLaTeX.com \displaystyle n = \lim_{x \to +\infty} \left[ \cfrac{x^3}{x^2-4}-x\right] = \cfrac{+\infty}{+\infty} - (+\infty) = \bm{+\infty - \infty}](https://mathority.org/wp-content/ql-cache/quicklatex.com-13478ac6f6fac958ec8b2a714c28bc3d_l3.png)
Mais on obtient l’indétermination ∞ – ∞. Il faut donc réduire les termes à un dénominateur commun. Pour ce faire, on multiplie et divise le x par le dénominateur de la fraction :
![Rendered by QuickLaTeX.com \displaystyle n = \lim_{x \to +\infty} \left[ \cfrac{x^3}{x^2-4}-\cfrac{x \cdot (x^2-4)}{(x^2-4)}\right] =\lim_{x \to +\infty} \left[ \cfrac{x^3}{x^2-4}-\cfrac{x^3-4x}{x^2-4}\right]](https://mathority.org/wp-content/ql-cache/quicklatex.com-5e939b43a3405ba644d4b60bb4bacadb_l3.png)
![]()
![]()
En bref, l’asymptote oblique est :
![]()
![]()
![]()
Pour étudier la monotonie de la fonction, il faut d’abord calculer sa dérivée :
![]()
![]()
Maintenant, nous fixons la dérivée égale à 0 et résolvons l’équation :
![]()
![]()
![]()
![]()
![]()
![Rendered by QuickLaTeX.com \displaystyle x^2\cdot(x^2-12) =0 \longrightarrow \begin{cases} x^2 =0 \ \longrightarrow \ \bm{x=0} \\[2ex] x^2-12=0 \ \longrightarrow \ x=\sqrt{12} \ \longrightarrow \ \bm{x= \pm 3,46} \end{cases}](https://mathority.org/wp-content/ql-cache/quicklatex.com-dc1f64cdcd293da4fee1ef02fff9a588_l3.png)
Nous représentons maintenant sur la ligne tous les points singuliers trouvés, c’est-à-dire les points qui n’appartiennent pas au domaine (x=-2 et x=+2) et ceux qui annulent la dérivée (x=0, x=-3,46 et x= +3,46) :

Et on évalue le signe de la dérivée dans chaque intervalle, pour savoir si la fonction augmente ou diminue. Nous prenons donc un point dans chaque intervalle (jamais les points singuliers) et regardons quel signe la dérivée a à ce point :
![]()
![]()
![]()
![]()
![]()
![]()
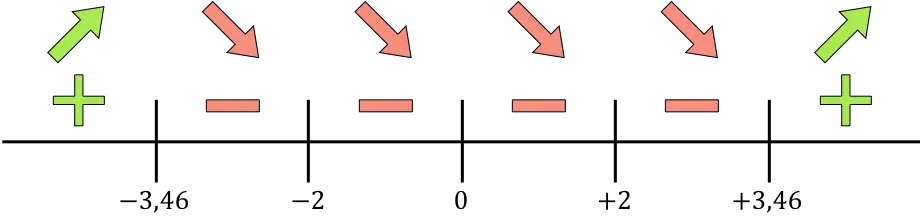
Si la dérivée est positive, cela signifie que la fonction augmente, et si la dérivée est négative, cela signifie que la fonction diminue. Par conséquent, les intervalles de croissance et de diminution sont :
Croissance:
![]()
Diminuer:
![]()
La fonction passe de croissante à décroissante à x=-3,46, donc x=-3,46 est un maximum de la fonction. Et la fonction passe de décroissante à croissante à x=3,46, donc x=3,46 est un minimum de la fonction.
On détermine les coordonnées Y des extrémités relatives :
![]()
![]()
Les extrêmes relatifs de la fonction sont donc :
Maximum sur le point
![]()
Minimum au point
![]()
Pour étudier la courbure de la fonction, on calcule la dérivée seconde de la fonction :
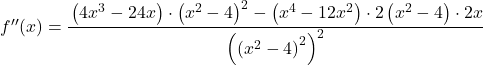
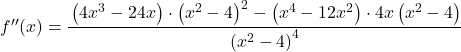
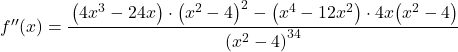
![]()
![]()
![]()
![]()
Maintenant, nous fixons la dérivée seconde égale à 0 et résolvons l’équation :
![]()
![]()
![]()
![]()
![]()
![Rendered by QuickLaTeX.com \displaystyle x\cdot(8x^2+96) =0 \longrightarrow \begin{cases} \bm{x =0} \\[2ex] 8x^2+96=0 \ \longrightarrow \ x^2=\cfrac{-96}{8}} = -12 \ \longrightarrow \ x= \sqrt{-12} \ \color{red}\bm{\times} \end{cases}](https://mathority.org/wp-content/ql-cache/quicklatex.com-31adba554b44aa92fd7227506440ccaf_l3.png)
![]() Il n’y a pas de solution puisqu’il n’existe pas de racine négative d’un nombre réel.
Il n’y a pas de solution puisqu’il n’existe pas de racine négative d’un nombre réel.
Nous représentons maintenant sur la ligne tous les points singuliers trouvés, c’est-à-dire les points qui n’appartiennent pas au domaine (x=-2 et x=+2) et ceux qui annulent la dérivée seconde (x=0) :

Et on évalue le signe de la dérivée seconde dans chaque intervalle, pour savoir si la fonction est concave ou convexe. Nous prenons donc un point dans chaque intervalle (jamais les points singuliers) et regardons quel signe la dérivée seconde a à ce point :
![]()
![]()
![]()
![]()

Si la dérivée seconde est positive, cela signifie que la fonction est convexe.
![]() , et si la dérivée seconde est négative cela signifie que la fonction est concave
, et si la dérivée seconde est négative cela signifie que la fonction est concave![]() . Les intervalles de concavité et de convexité sont donc :
. Les intervalles de concavité et de convexité sont donc :
Convexe
![]() :
:![]()
Concave
![]() :
:![]()
Cependant, bien qu’il y ait un changement de courbure à x=-2 et x=+2, ce ne sont pas des points d’inflexion. Parce que x=-2 et x=+2 n’appartiennent pas au domaine de la fonction. Par contre, à x=0 il y a un changement de courbure (la fonction passe de convexe à concave) et cela appartient à la fonction, donc x=0 est un point d’inflexion.
Nous substituons les points d’inflexion trouvés dans la fonction d’origine pour trouver l’autre coordonnée du point d’inflexion :
![]()
Les tournants de la fonction sont donc :
Points tournants :
![]()
Enfin, sur la base de toutes les informations que nous avons calculées, nous représentons la fonction :
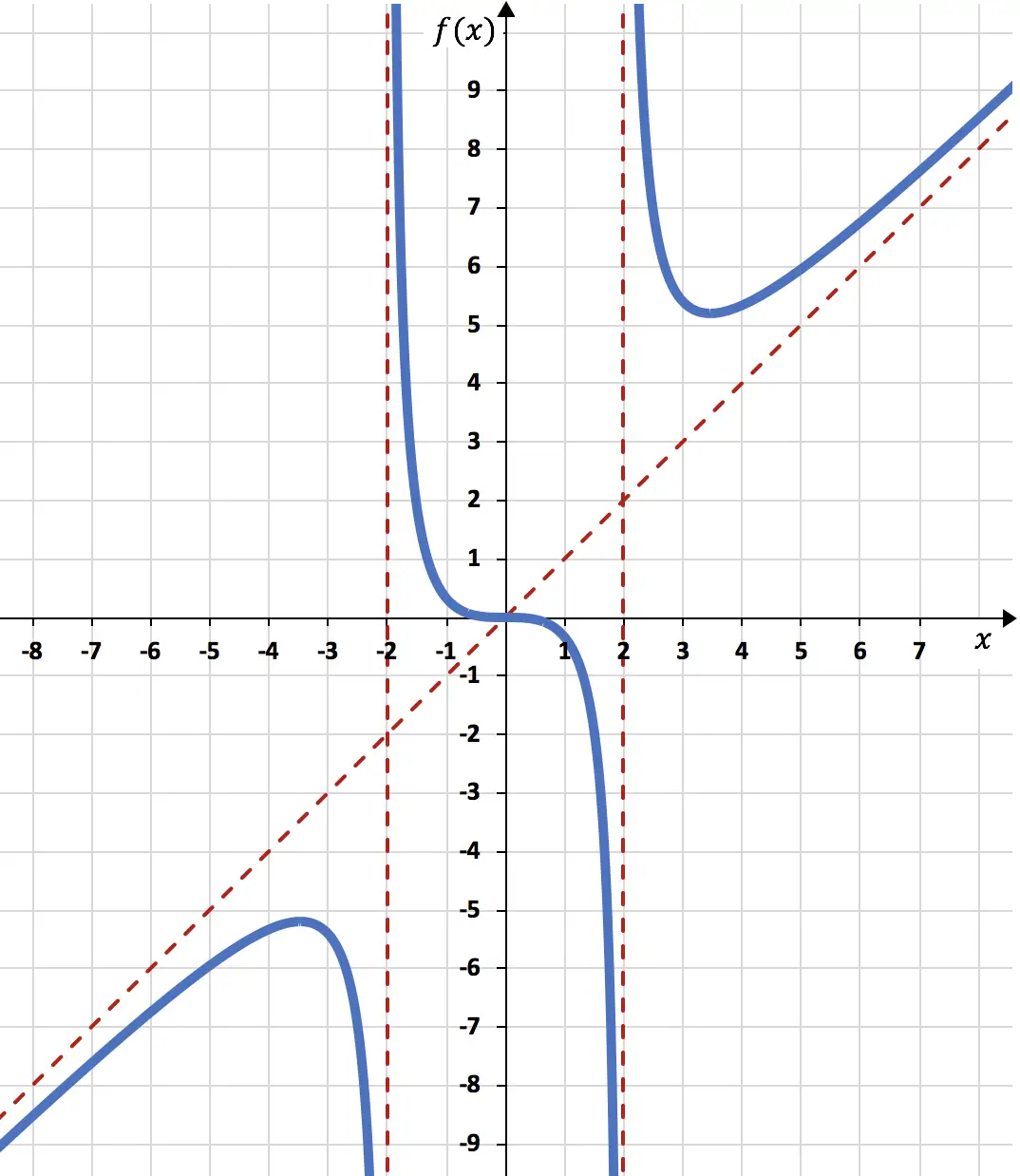
Commentaire : Notez que la fonction croise l’asymptote oblique au point
![]() En effet, les asymptotes obliques déterminent avant tout le comportement de la fonction lorsque x tend vers +∞ et -∞, en effet, la fonction ne traverse jamais l’asymptote oblique à droite du graphe (x→+∞) et à gauche du graphique (x→-∞). Il est néanmoins très rare que la fonction traverse l’asymptote oblique au milieu, c’est un cas très particulier.
En effet, les asymptotes obliques déterminent avant tout le comportement de la fonction lorsque x tend vers +∞ et -∞, en effet, la fonction ne traverse jamais l’asymptote oblique à droite du graphe (x→+∞) et à gauche du graphique (x→-∞). Il est néanmoins très rare que la fonction traverse l’asymptote oblique au milieu, c’est un cas très particulier.