Vous trouverez ici ce qu’est la fonction d’identité. De plus, vous pourrez voir comment représenter graphiquement la fonction identité et quelles sont ses caractéristiques.
Qu’est-ce qu’une fonction identité ?
Une fonction d’identité est cette fonction qui a comme image la même valeur que l’argument. La fonction d’identité peut être exprimée avec le terme id .
Par conséquent, l’expression mathématique de la fonction d’identité est :
![]()
Par exemple, l’image de la fonction identité pour x=1 vaut 1, l’image de x=2 vaut 2, l’image de x=3 vaut 3,…
![Rendered by QuickLaTeX.com \begin{array}{c}f(1)=1\\[2ex]f(2)=2\\[2ex]f(3)=3\\ \bm{\vdots}\end{array}](https://mathority.org/wp-content/ql-cache/quicklatex.com-4b85e48e3f36d1eb4271b265aaf35bef_l3.png)
La fonction identité est un exemple de fonction linéaire. Dans le lien suivant, vous pouvez voir plus d’exemples de ce type de fonctions :
➤ Voir : exemples de fonctions linéaires
Représentation graphique de la fonction identité
Le graphique de la fonction identité correspond à une droite qui est la bissectrice des premier et troisième quadrants.
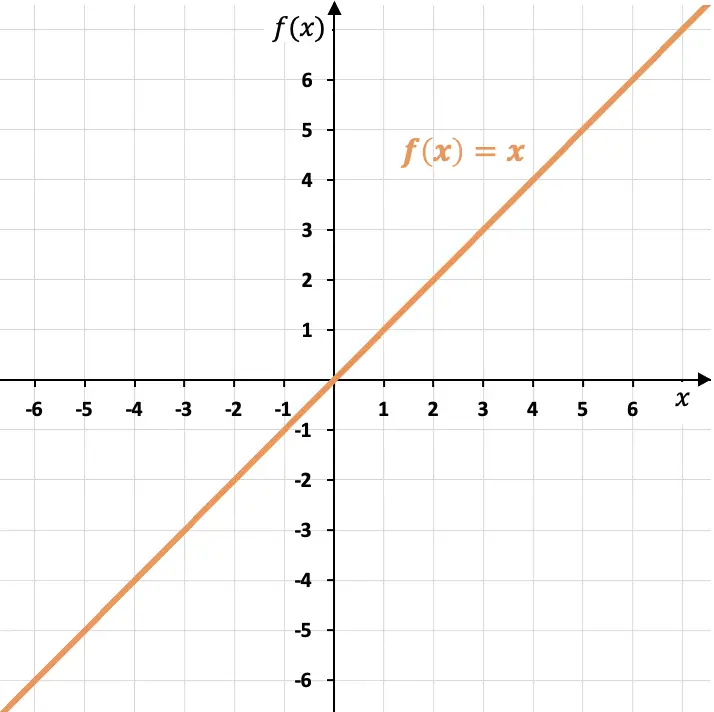
Comme vous pouvez le voir, la fonction identité passe par l’origine des coordonnées (point (0,0)) et a une pente égale à l’unité (m=1), puisqu’une unité de la variable croît et pour chaque valeur de la variable indépendante X. De plus, la fonction d’identité forme un angle de 45º avec l’axe X.
Caractéristiques de la fonction identité
La fonction d’identité a les propriétés suivantes :
- Le domaine de la fonction d’identité est tous les nombres réels :
![]()
- La plage (ou plage) de la fonction d’identité est également constituée de tous les nombres réels :
![]()
- La fonction identité est une fonction continue et bijective.
- De plus, la fonction identité consiste en une fonction impaire, ce qui signifie qu’il s’agit d’une fonction symétrique par rapport à l’origine des coordonnées.
![]()
➤ Voir : fonction symétrique impaire
- La fonction identité est croissante sur tout son domaine, et sa pente est égale à 1.
![]()
- Coupe l’axe des abscisses (axe OX) et l’axe des ordonnées (axe Y) au même point : l’origine des coordonnées.
![]()
- Elle peut être classée comme une fonction polynomiale du premier degré.
- La fonction identité agit comme un élément neutre de la composition des fonctions . De sorte que toute fonction composée avec la fonction identité aboutit à la fonction elle-même.
![]()
- La valeur
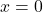 est la seule racine de ce type de fonction.
est la seule racine de ce type de fonction.
- La limite de la fonction d’identité lorsque x tend vers plus l’infini ou moins l’infini donne respectivement plus l’infini et moins l’infini :
![]()
![]()
- La fonction identité n’a donc pas d’asymptote.
- La dérivée de la fonction identité est la fonction constante de valeur 1 :
![]()
- L’intégrale de la fonction identité est la fonction quadratique :
![]()
➤ Voir : formule de la fonction quadratique