Vous trouverez ici comment dériver l’arc tangente hyperbolique d’une fonction. Vous pourrez également voir des exemples résolus de ce type de dérivées trigonométriques et, enfin, nous vous montrerons la formule de la dérivée de l’arc tangente hyperbolique.
Formule de la dérivée de l’arc tangente hyperbolique
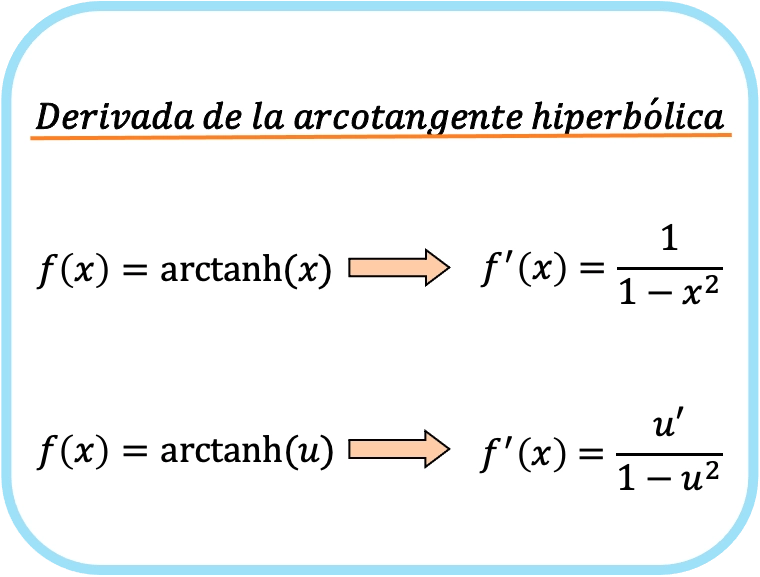
La dérivée de l’arc tangente hyperbolique de x est un sur un moins x au carré.
![]()
Par conséquent, la dérivée de l’arc tangente hyperbolique d’une fonction est égale au quotient de la dérivée de cette fonction divisé par un moins ladite fonction au carré.
![]()
En fait, les deux formules sont identiques, mais dans la seconde, la règle de la chaîne est appliquée. Par exemple, remplacer x par u nous donne exactement la première formule puisque la dérivée de x est 1.
Tout comme l’arc tangente est la fonction inverse de la tangente, l’arc tangente hyperbolique est l’inverse de la tangente hyperbolique. Même ainsi, leurs dérivées sont très différentes, vous pouvez vérifier la dérivée de cette fonction trigonométrique ici :
➤ Voir : formule de la dérivée de la tangente hyperbolique
Exemples de dérivée de l’arc tangente hyperbolique
Exemple 1
![]()
Logiquement, il faut appliquer la règle de la dérivée de l’arc tangente hyperbolique :
![]()
La dérivée de 2x est 2, donc au numérateur de la fraction il faut mettre un deux et au dénominateur un moins 2x au carré :
![]()
Exemple 2
![]()
Pour résoudre la dérivée de cette fonction, nous devons utiliser la formule de la dérivée de l’arc tangente hyperbolique.
![]()
De plus, la fonction de l’argument de l’arc tangente hyperbolique est une fonction composée, nous devrons donc également appliquer la règle de chaîne :
![]()
Preuve de la dérivée de l’arc tangente hyperbolique
Dans cette dernière section, nous allons démontrer la formule de la dérivée de l’arc tangente hyperbolique.
![]()
Puisque l’arc tangente hyperbolique est la tangente hyperbolique inversée, nous pouvons exprimer l’égalité précédente d’une autre manière :
![]()
Maintenant, nous dérivons les deux côtés de l’équation :
![]()
Nous vous dédouanons :
![]()
Par contre, on sait que la différence des carrés du cosinus hyperbolique et du sinus hyperbolique donne 1. On peut donc transformer l’expression précédente en une fraction :
![]()
![]()
On divise tous les termes de la fraction par le carré du cosinus hyperbolique :
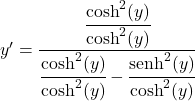
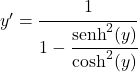
Le quotient du sinus hyperbolique entre le cosinus hyperbolique est égal à la tangente hyperbolique, donc :
![]()
![]()
Mais, comme nous l’avons vu au début de la preuve, la tangente hyperbolique est équivalente à la variable x, nous pouvons donc substituer l’expression obtenant ainsi la formule de la dérivée de l’arc tangente hyperbolique :
![]()