Dérivée de la tangente hyperbolique

Vous trouverez ici quelle est la dérivée de la tangente hyperbolique d’une fonction. De plus, vous pourrez voir plusieurs exemples résolus de dérivées de tangentes hyperboliques. Et enfin, nous vous montrons la formule de la dérivée de la tangente hyperbolique.

Formule de la dérivée de la tangente hyperbolique

La dérivée de la tangente hyperbolique de x est égale à 1 divisé par le carré du cosinus hyperbolique de x. La dérivée de la tangente de x est aussi équivalente au carré de la sécante hyperbolique de x, et à 1 moins le carré de la tangente hyperbolique de x.

$\begin{array}{c}f(x)=\text{tanh}(x)\\[1.5ex]\color{orange}\bm{\downarrow}\color{black}\\ f'(x)=\cfrac{1}{\text{cosh}^2(x)}=\text{sech}^2(x)=1-\text{tanh}^2(x)\end{array}$

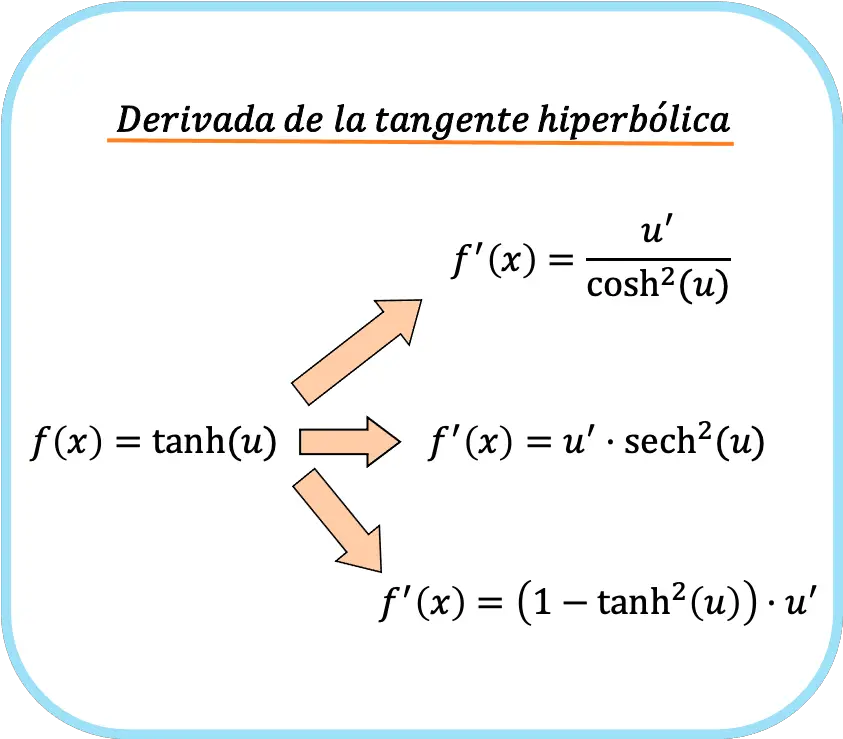
D’autre part, si dans l’argument de la fonction nous avons une fonction différente de x, nous devons appliquer la règle de la chaîne. Et puis les trois formules pour la dérivée de la tangente hyperbolique sont :

$\begin{array}{c}f(x)=\text{tanh}(u)\\[1.5ex]\color{orange}\bm{\downarrow}\color{black}\\ f'(x)=\cfrac{u'}{\text{cosh}^2(u)}=\text{sech}^2(u)\cdot u'=\left(1-\text{tanh}^2(u)\right)\cdot u'\end{array}$

Cela ne signifie pas que chaque fois que nous dérivons la tangente hyperbolique, nous devons utiliser les trois formules, mais plutôt que nous pouvons utiliser n’importe laquelle d’entre elles pour la dériver. Ainsi, selon la fonction de l’argument de la tangente hyperbolique, il sera préférable d’utiliser une formule ou une autre. Vous trouverez ci-dessous plusieurs exemples dans lesquels vous pouvez voir comment la tangente hyperbolique d’une fonction est dérivée.

La dérivée de la tangente hyperbolique est presque identique à la dérivée de la tangente, mais elle a un petit détail qui les rend totalement différentes. Vous pouvez voir quelle est la différence dans le lien suivant :

➤ Voir : formule dérivée tangente

Exemples de dérivée de la tangente hyperbolique

Après avoir vu quelle est la formule de la dérivée de la tangente hyperbolique, voici plusieurs exemples résolus de dérivées de ce type de fonctions trigonométriques afin que vous compreniez parfaitement comment dériver la tangente hyperbolique.

Exemple 1 : Dérivée de la tangente hyperbolique de 2x

$f(x)=\text{tanh}(2x)$

Pour dériver la tangente hyperbolique dans cet exemple, nous utiliserons la formule du cosinus hyperbolique, bien que vous puissiez bien sûr utiliser celle que vous préférez.

$f(x)=\text{tanh}(u)\quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=\cfrac{u'}{\text{cosh}^2(u)}$

Nous savons que la dérivée de 2x est 2, donc la dérivée de la fonction entière est :

$f(x)=\text{tanh}(2x)\quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=\cfrac{2}{\text{cosh}^2(2x)}$

Exemple 2 : Dérivée de la tangente hyperbolique de x au carré

$f(x)=\text{tanh}(x^2)$

La règle de la dérivée de la tangente hyperbolique d’une fonction est :

$f(x)=\text{tanh}(u)\quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=\cfrac{u'}{\text{cosh}^2(u)}$

D’une part, nous dérivons la fonction de l’argument x ² , ce qui donne 2x, puis nous résolvons la dérivée de la fonction entière à l’aide de la formule :

$f(x)=\text{tanh}(x^2)\quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=\cfrac{2x}{\text{cosh}^2(x^2)}$

Exemple 3 : Dérivée de la tangente hyperbolique au cube

$f(x)=\text{tanh}^3(7x^2)$

Dans ce cas, il faut dériver la tangente hyperbolique d’une fonction qui, de plus, est élevée à une puissance. Nous devons donc utiliser la formule de la dérivée d’une fonction potentielle, la règle de la dérivée de la tangente hyperbolique et la règle de la chaîne :

$f'(x)=3\text{tanh}^2(7x^2)\cdot \cfrac{14x}{\text{cosh}^2(7x^2)}}=\cfrac{42x\cdot \text{tanh}^2(7x^2)}{\text{cosh}^2(7x^2)}}$

Preuve de la dérivée de la tangente

Dans cette section, nous démontrerons la formule de la dérivée de la tangente hyperbolique. Et, pour cela, nous partirons de l’identité trigonométrique qui relie les trois rapports trigonométriques hyperboliques :

$\text{tanh}(x)=\cfrac{\text{senh}(x)}{\text{cosh}(x)}$

➤ Remarque : Pour comprendre la preuve, vous devez savoir quelle est la dérivée du sinus hyperbolique et quelle est la dérivée du cosinus hyperbolique . C’est pourquoi nous vous recommandons de visiter les pages liées avant de continuer.

Maintenant, appliquons la formule de la dérivée d’un quotient :

$\displaystyle\left(\text{tanh}(x)\right)'=\left(\frac{\text{senh}(x)}{\text{cosh}(x)}\right)'$

$\text{tanh}'(x)=\cfrac{\text{cosh}(x)\cdot \text{cosh}(x)-\text{senh}(x)\text{senh}(x) }{\text{cosh}^2(x)}$

$\text{tanh}'(x)=\cfrac{\text{cosh}^2(x)-\text{senh}^2(x)}{\text{cosh}^2(x)}$

On réduit l’expression du numérateur de la fraction à l’aide de la formule suivante :

$\text{cosh}^2(x)-\text{senh}^2(x)=1$

$\text{tanh}'(x)=\cfrac{1}{\text{cosh}^2(x)}$

Comme vous pouvez le voir, l’égalité précédente correspond à la première formule de la dérivée de la tangente hyperbolique. De même, la sécante hyperbolique est l’inverse multiplicatif du cosinus hyperbolique, donc la deuxième formule est également prouvée :

$\text{tanh}'(x)=\text{sech}^2(x)$

Enfin, nous pouvons arriver à la troisième règle de la dérivée de la tangente hyperbolique en convertissant la fraction de l’étape précédente en une soustraction de fractions :

$\text{tan}'(x)=\cfrac{\text{cosh}^2(x)-\text{senh}^2(x)}{\text{cosh}^2(x)}$

$\text{tanh}'(x)=\cfrac{\text{cosh}^2(x)}{\text{cosh}^2(x)}-\cfrac{\text{senh}^2(x)}{\text{cosh}^2(x)}$

$\text{tanh}'(x)=1-\text{tanh}^2(x)$