Vous trouverez ici comment dériver le sinus hyperbolique (formule). De plus, vous pourrez voir plusieurs exemples résolus de la dérivée du sinus hyperbolique. Et enfin, nous prouvons la formule de la dérivée de ce type de fonction trigonométrique.
Formule dérivée du sinus hyperbolique
La dérivée du sinus hyperbolique de x est le cosinus hyperbolique de x.
![]()
Par conséquent, la dérivée du sinus hyperbolique d’une fonction est égale au produit du cosinus hyperbolique de la fonction par la dérivée de cette fonction.
![]()
En fait, les deux formules ci-dessus sont les mêmes, la seule différence est que dans la deuxième formule, nous appliquons la règle de la chaîne. Et puisque la dérivée de x est 1, cela ne change pas la fonction.
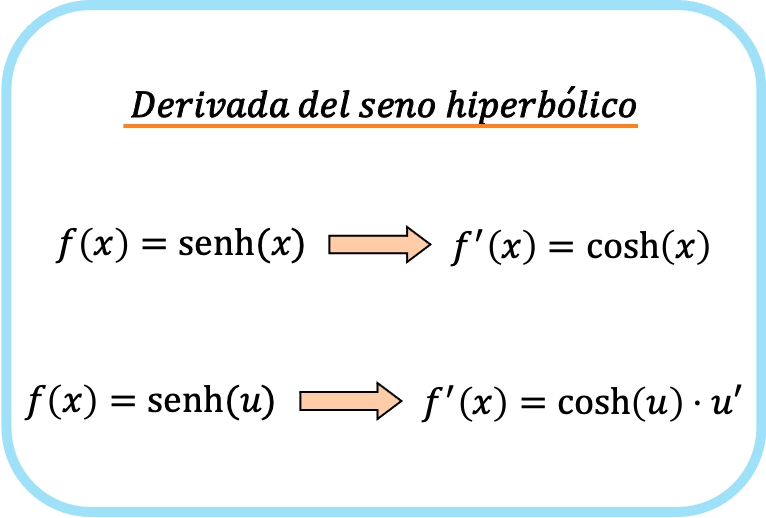
Comme vous pouvez le voir, la formule de la dérivée du sinus hyperbolique est très similaire à la formule de la dérivée du sinus .
Exemples de la dérivée du sinus hyperbolique
Une fois que nous avons déjà vu ce qu’est la formule de la dérivée du sinus hyperbolique, nous procédons maintenant à la résolution de plusieurs exemples de la dérivée du sinus hyperbolique. Donc, vous n’avez sûrement aucun doute sur la façon dont cela est fait.
Exemple 1 : Dérivée du sinus hyperbolique de 2x
![]()
Dans ce cas, dans l’argument du sinus hyperbolique, nous avons une fonction différente de x, par conséquent, nous devons utiliser la formule de la dérivée du sinus hyperbolique avec la règle de la chaîne pour trouver la dérivée :
![]()
La dérivée de 2x est 2, donc la dérivée du sinus hyperbolique de 2x sera le cosinus hyperbolique de 2x fois 2.
![]()
Exemple 2 : Dérivée du sinus hyperbolique de x au carré
![]()
La formule de la dérivée de la fonction sinus hyperbolique est :
![]()
D’autre part, la dérivée de la fonction quadratique x 2 est 2x. La dérivée de la fonction entière est donc :
![]()
Preuve de la formule de la dérivée du sinus hyperbolique
Enfin, nous allons démontrer la formule de la dérivée du sinus hyperbolique. Pour ce faire, nous partirons de la définition mathématique du sinus hyperbolique :
![]()
On déduit maintenant les deux côtés de l’égalité :
![]()
Pour dériver le côté droit de l’équation, nous utiliserons la formule de la dérivée d’une division :
![]()
➤ Voir : dérivée de la fonction exponentielle de base e
Et précisément nous sommes arrivés à l’expression qui définit le cosinus hyperbolique. De sorte que la dérivée du sinus hyperbolique est prouvée :
![]()