▷ Dérivée de la tangente (formule et exercices résolus)

Vous découvrirez ici comment la fonction tangente est dérivée. De plus, vous pourrez voir des exemples de dérivée de la tangente et même vous entraîner avec des exercices résolus étape par étape. Enfin, nous démontrons également la formule de la dérivée de la tangente et vous montrons la formule de la dérivée de la tangente inverse.

Quelle est la dérivée de la tangente ?

La dérivée de la tangente de x est égale à 1 sur le carré du cosinus de x. La dérivée de la tangente de x est également équivalente au carré de la sécante de x, et 1 plus le carré de la tangente de x.

$\begin{array}{c}f(x)=\text{tan}(x)\\[1.5ex]\color{orange}\bm{\downarrow}\color{black}\\ f'(x)=\cfrac{1}{\text{cos}^2(x)}=\text{sec}^2(x)=1+\text{tan}^2(x)\end{array}$

Toutes les expressions sont équivalentes, donc la fonction tangente a trois formules possibles pour la dériver.

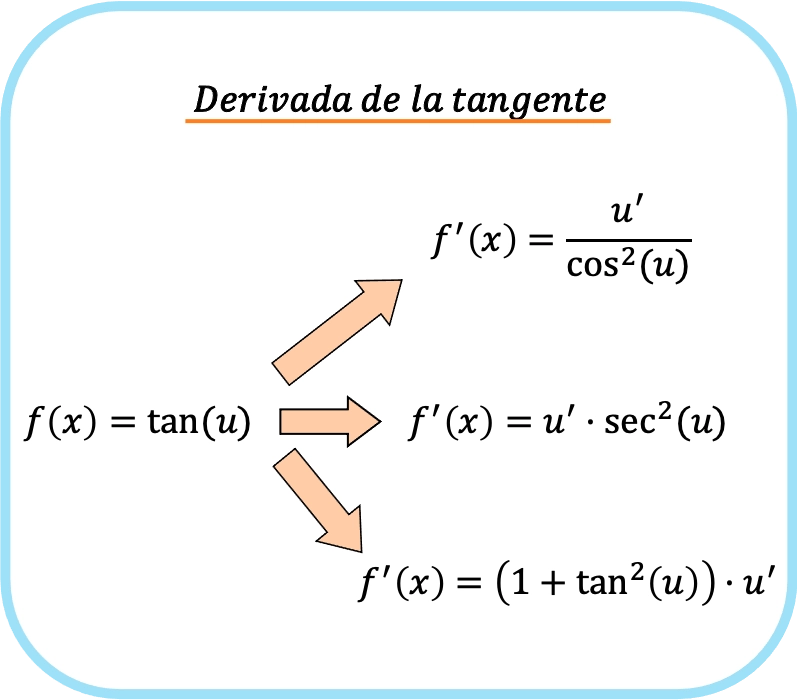
En revanche, lorsque dans l’argument tangente nous avons une fonction différente de x (appelons-la u), nous devons appliquer la règle de la chaîne. La dérivée de la tangente de u est donc :

$\begin{array}{c}f(x)=\text{tan}(u)\\[1.5ex]\color{orange}\bm{\downarrow}\color{black}\\ f'(x)=\cfrac{u'}{\text{cos}^2(u)}=\text{sec}^2(u)\cdot u'=\left(1+\text{tan}^2(u)\right)\cdot u'\end{array}$

En bref, la règle de dérivée tangente peut être résumée comme suit :

Exemples de dérivée de la tangente

Étant donné la formule de la dérivée de la tangente, dans cette section nous allons résoudre plusieurs exemples de ce type de dérivées trigonométriques afin que vous compreniez comment dériver la fonction tangente.

Exemple 1 : Dérivée de la tangente de 2x

$f(x)=\text{tan}(2x)$

Pour calculer la dérivée de la tangente, vous pouvez utiliser l’une des trois formules que nous avons vues ci-dessus. Dans ce cas, nous utiliserons la formule du cosinus :

$f(x)=\text{tan}(u)\quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=\cfrac{u'}{\text{cos}^2(u)}$

La fonction 2x est linéaire, donc sa dérivée est 2. Donc la dérivée de la tangente de 2x est 2 sur le carré du cosinus de 2x :

$f(x)=\text{tan}(2x)\quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=\cfrac{2}{\text{cos}^2(2x)}$

Exemple 2 : Dérivée de la tangente de x au carré

$f(x)=\text{tan}(x^2)$

Dans cet exemple, la fonction de l’argument tangent n’est pas un x, mais une fonction avec une dérivée. Ce qui signifie que nous devons appliquer la règle de la chaîne pour le dériver.

$f(x)=\text{tan}(u)\quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=\cfrac{u'}{\text{cos}^2(u)}$

La dérivée de x au carré est 2x, donc la dérivée de la tangente de x ² est :

$f(x)=\text{tan}(x^2) \quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=\cfrac{2x}{\text{cos}^2(x^2)}$

Exemple 3 : Dérivée de la tangente au cube

$f(x)=\text{tan}^3(9x^2-4x)$

Dans ce problème, nous avons une fonction composite, nous devrons donc également utiliser la règle de chaîne pour différencier la tangente.

$f(x)=\text{tan}(u)\quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=\cfrac{u'}{\text{cos}^2(u)}$

De plus, la tangente est élevée à la puissance 3, ce qui signifie qu’avant d’appliquer la formule de la dérivée de la tangente il faut utiliser la formule de la dérivée d’une puissance :

$\begin{aligned}f'(x)&=3\text{tan}^2(9x^2-4x)\cdot \cfrac{18x-4}{\text{cos}^2(9x^2-4x)} \\[2ex]&=\cfrac{3\text{tan}^2(9x^2-4x)\cdot(18x-4)}{\text{cos}^2(9x^2-4x)}\end{aligned}$

Dérivée de la tangente inverse

Comme toute fonction inverse, la fonction tangente a également un inverse, la fonction arctangente. Bien que la formule pour la dériver ne soit pas similaire à la formule tangente, nous vous la montrons car elle peut être utile dans certains cas.

La dérivée de la tangente inverse d’une fonction est le quotient de la dérivée de la fonction divisée par un plus ladite fonction au carré

$f(x)=\text{tan}^{-1}(u) \quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=\cfrac{u'}{1+u^2}$

Par exemple, la dérivée de la tangente inverse de 3x est la suivante :

$f(x)=\text{tan}^{-1}(3x) \quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=\cfrac{3}{1+(3x)^2}=\cfrac{3}{1+9x^2}$

Exercices résolus sur la dérivée de la tangente

Calculez la dérivée des fonctions tangentes suivantes :

$\text{A) } f(x)=\text{tan}(3x)$

$\text{B) } f(x)=\text{tan}(x^3-10x^2+8)$

$\text{C) } \displaystyle f(x)=\text{tan}^2\left(\frac{x}{2}\right)$

$\text{D) } f(x)=\text{tan}\left(e^{2x}\right)$

$\text{E) } f(x)=\text{tan}\bigl(\ln(4x)\bigr)$

$\text{F) } f(x)=\text{tan}\left(\sqrt{3x}\right)$

Voir la solution

$\text{A) } f'(x)=\cfrac{3}{\text{cos}^2(3x)}$

$\text{B) } f'(x)=\cfrac{3x^2-20x}{\text{cos}^2(x^3-10x^2+8)}$

$\text{C) } \displaystyle f'(x)=2\text{tan}\left(\frac{x}{2}\right)\cdot \frac{1}{\text{cos}^2\left(\frac{x}{2}\right)}\cdot \frac{1}{2}=\frac{\text{tan}\left(\frac{x}{2}\right)}{\text{cos}^2\left(\frac{x}{2}\right)}$

$\text{D) } f'(x)=\cfrac{2e^{2x}}{\text{cos}^2(e^{2x})}$

$\text{E) } f'(x)=\cfrac{\frac{4}{4x}}{\text{cos}^2\bigl(\ln(4x)\bigr)}=\cfrac{1}{x\cdot\text{cos}^2\bigl(\ln(4x)\bigr)}$

$\text{F) } f'(x)=\cfrac{\frac{3}{2\sqrt{3x}}}{\text{cos}^2\left(\sqrt{3x}\right)}=\cfrac{3}{2\sqrt{3x}\cdot \text{cos}^2\left(\sqrt{3x}\right)}$

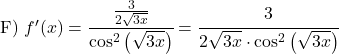
Preuve de la dérivée de la tangente

Afin que vous puissiez vérifier qu’il ne s’agit pas d’une expression inventée, dans cette section, nous allons démontrer la formule de la dérivée de la tangente en utilisant la définition mathématique de la tangente.

Pour ce faire, nous partirons de l’identité trigonométrique qui relie les trois rapports trigonométriques :

$\text{tan}(x)=\cfrac{\text{sen}(x)}{\text{cos}(x)}$

Si nous utilisons la formule de la dérivée d’une division , la dérivée serait :

$\displaystyle\left(\text{tan}(x)\right)'=\left(\frac{\text{sen}(x)}{\text{cos}(x)}\right)'$

$\text{tan}'(x)=\cfrac{\text{cos}(x)\cdot \text{cos}(x)+\text{sen}(x)\text{sen}(x) }{\text{cos}^2(x)}$

$\text{tan}'(x)=\cfrac{\text{cos}^2(x)+\text{sen}^2(x)}{\text{cos}^2(x)}$

Mais, en utilisant l’identité trigonométrique fondamentale, nous savons que le carré du sinus plus le carré du cosinus vaut 1 :

$\text{sen}^2(x)+\text{cos}^2(x)=1$

$\text{tan}'(x)=\cfrac{1}{\text{cos}^2(x)}$

Et ainsi nous sommes déjà arrivés à la première formule de la dérivée de la tangente. De plus, la sécante est l’inverse multiplicatif du cosinus, donc la deuxième expression est également prouvée :

$\text{tan}'(x)=\text{sec}^2(x)$

Enfin, la troisième règle de la dérivée tangente peut être prouvée en transformant la fraction de l’étape précédente en une somme de fractions :

$\text{tan}'(x)=\cfrac{\text{cos}^2(x)+\text{sen}^2(x)}{\text{cos}^2(x)}$

$\text{tan}'(x)=\cfrac{\text{cos}^2(x)}{\text{cos}^2(x)}+\cfrac{\text{sen}^2(x)}{\text{cos}^2(x)}$

$\text{tan}'(x)=1+\text{tan}^2(x)$

Quelle est la dérivée de la tangente ?

Exemples de dérivée de la tangente

Exemple 1 : Dérivée de la tangente de 2x

Exemple 2 : Dérivée de la tangente de x au carré

Exemple 3 : Dérivée de la tangente au cube

Dérivée de la tangente inverse

Exercices résolus sur la dérivée de la tangente

Preuve de la dérivée de la tangente

Leave a Comment Cancel Reply