▷ Dérivée de la cotangente (formule et exemples)

Dans cet article, nous verrons comment dériver la cotangente d’une fonction. Vous trouverez des exemples de dérivée de la cotangente et même des exercices résolus étape par étape. Enfin, nous prouvons la formule de la dérivée de la cotangente.

Formule pour la dérivée de la cotangente

La dérivée de la cotangente de x est égale à moins un sur le carré du sinus de x. La dérivée de la cotangente de x équivaut également à moins le carré de la cosécante de x, et moins la somme de un plus le carré de la cotangente de x.

$\begin{array}{c}f(x)=\text{cotg}(x)\\[1.5ex]\color{orange}\bm{\downarrow}\color{black}\\ f'(x)=-\cfrac{1}{\text{sen}^2(x)}=-\text{cosec}^2(x)=-\left(1+\text{cotg}^2(x)\right)\end{array}$

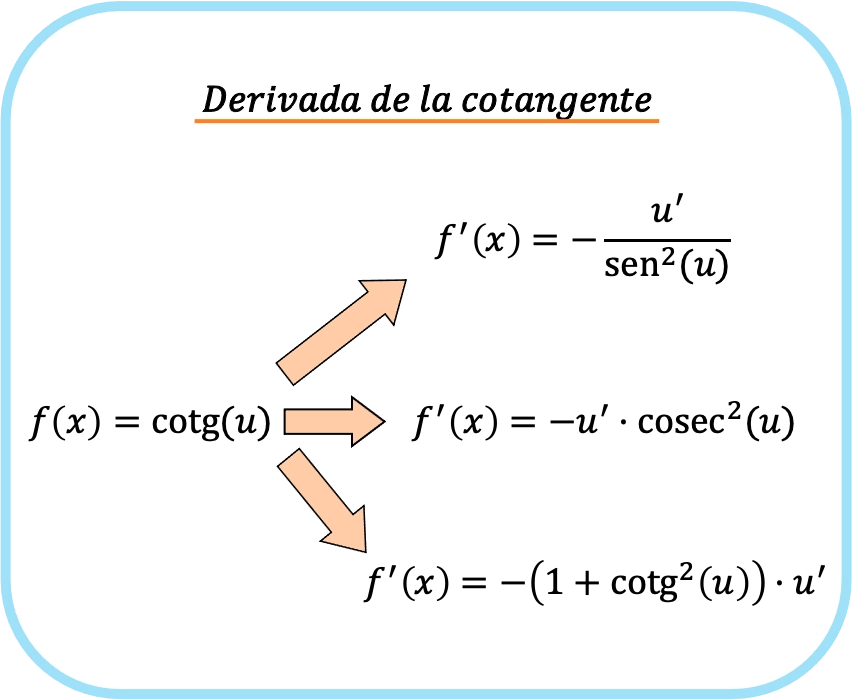
Si l’argument cotangent est une fonction différente de x, les formules pour la dérivée de la cotangente d’une fonction sont les mêmes que les précédentes, mais en multipliant les expressions par la dérivée de la fonction de l’argument.

$\begin{array}{c}f(x)=\text{cotg}(u)\\[1.5ex]\color{orange}\bm{\downarrow}\color{black}\\ f'(x)=-\cfrac{u'}{\text{sen}^2(u)}=-u' \cdot \text{cosec}^2(u)=-u' \cdot \left(1+\text{cotg}^2(u)\right)\end{array}$

Cela signifie qu’il existe trois formules différentes pour trouver la dérivée de la cotangente. Mais, logiquement, il n’est pas nécessaire d’utiliser les trois formules, mais vous pouvez le dériver avec la formule que vous préférez.

Exemples de dérivée de la cotangente

Maintenant que nous avons vu la formule de la dérivée de la cotangente d’une fonction, dans cette section nous allons résoudre plusieurs exemples de ce type de dérivées trigonométriques.

Exemple 1 : Dérivée de la cotangente de 2x

Dans cet exemple nous verrons quelle est la dérivée de la cotangente de la fonction 2x.

$f(x)=\text{cotg}(2x)$

Comme nous l’avons vu, pour calculer la dérivée de la cotangente, vous pouvez utiliser l’une des trois formules vues ci-dessus. Dans ce cas, nous utiliserons la formule sinusoïdale :

$f(x)=\text{cotg}(u)\quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=-\cfrac{u'}{\text{sen}^2(u)}$

Puisque 2x est un terme du premier degré, sa dérivée est 2. Donc la dérivée de la cotangente de 2x est moins deux divisé par le carré du sinus de 2x :

$f(x)=\text{cotg}(2x)\quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=-\cfrac{2}{\text{sen}^2(2x)}$

Exemple 2 : Dérivée de la cotangente de x au carré

Dans le deuxième exemple nous déterminerons ce que vaut la dérivée de la cotangente de x au carré.

$f(x)=\text{cotg}(x^2)$

Dans cet exemple, la fonction de l’argument cotangente n’est pas un x, nous devons donc appliquer la règle de la chaîne pour différencier la cotangente.

$f(x)=\text{cotg}(u)\quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=-\cfrac{u'}{\text{sen}^2(u)}$

La dérivée de x au carré est 2x, donc la dérivée de la cotangente de x ² est :

$f(x)=\text{cotg}(x^2)\quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=-\cfrac{2x}{\text{sen}^2(x^2)}$

Exemple 3 : Dérivée de la cotangente au cube

Enfin, nous trouverons combien vaut la dérivée de la cotangente au cube d’une fonction polynomiale :

$f(x)=\text{cotg}^3(x^5-6x^2+10)$

Dans ce cas, nous avons une composition de fonctions, nous devons donc utiliser la règle de chaîne avec la formule de la dérivée d’une puissance pour trouver la dérivée de la cotangente :

$\displaystyle f'(x)=-3\cdot\text{cotg}^2(x^5-6x^2+10)\cdot\frac{5x^4-12x}{\text{sen}^2(x^5-6x^2+10)}$

Exercices résolus sur la dérivée de la cotangente

Calculez la dérivée des fonctions cotangentes suivantes :

$\text{A) } f(x)=\text{cotg}(5x)$

$\text{B) } f(x)=\text{cotg}(2x^4+10x-3)$

$\text{C) } \displaystyle f(x)=\text{cotg}^5\left(\frac{x}{2}\right)$

$\text{D) } f(x)=\text{cotg}\left(e^{x^2}\right)$

$\text{E) } f(x)=\text{cotg}\bigl(\ln(x^2)\bigr)$

$\text{F) } f(x)=\text{cotg}\left(\sqrt{8x}\right)$

Voir la solution

$\text{A) } f'(x)=-\cfrac{5}{\text{sen}^2(5x)}$

$\text{B) } f'(x)=-\cfrac{8x+10}{\text{sen}^2(2x^4+10x-3)}$

$\text{C) } \displaystyle f'(x)=5\cdot \text{cotg}^4\left(\frac{x}{2}\right)\cdot \left(-\frac{1}{\text{sen}^2\left(\frac{x}{2}\right)}\right)\cdot \frac{1}{2}=-\frac{5\cdot \text{cotg}^4\left(\frac{x}{2}\right)}{2\cdot \text{sen}^2\left(\frac{x}{2}\right)}$

$\text{D) } f'(x)=-\cfrac{2x\cdot e^{x^2}}{\text{sen}^2(e^{x^2})}$

$\text{E) } f'(x)=-\cfrac{\cfrac{2x}{x^2}}{\text{sen}^2\bigl(\ln(x^2)\bigr)}=-\cfrac{2}{x\cdot\text{sen}^2\bigl(\ln(x^2)\bigr)}$

$\text{F) } f'(x)=-\cfrac{\frac{8}{2\sqrt{8x}}}{\text{sen}^2\left(\sqrt{8x}\right)}=-\cfrac{4}{\sqrt{8x}\cdot \text{sen}^2\left(\sqrt{8x}\right)}$

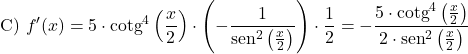
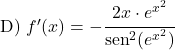
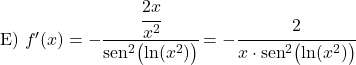
Preuve de la dérivée de la cotangente

Dans cette dernière section, nous démontrerons la formule de la dérivée de la cotangente. Pour ce faire, nous partirons de la définition mathématique de la fonction cotangente, qui est égale au cosinus divisé par le sinus :

$\text{cotg}(x)=\cfrac{\text{cos}(x)}{\text{sen}(x)}$

Maintenant, nous dérivons la fonction en appliquant la règle de la dérivée d’un quotient ;

$\displaystyle\bigl(\text{cotg}(x)\bigr)'=\left(\frac{\text{cos}(x)}{\text{sen}(x)}\right)'$

$\text{cotg}'(x)=\cfrac{-\text{sen}(x)\cdot \text{sen}(x)-\text{cos}(x)\cdot \text{cos}(x) }{\text{sen}^2(x)}$

$\text{cotg}'(x)=\cfrac{-\text{sen}^2(x)-\text{cos}^2(x)}{\text{sen}^2(x)}$

Nous prenons le facteur commun au dénominateur et supprimons le signe négatif de la fraction :

$\text{cotg}'(x)=\cfrac{-\bigl(\text{sen}^2(x)+\text{cos}^2(x)\bigr)}{\text{sen}^2(x)}$

$\text{cotg}'(x)=-\cfrac{\text{sen}^2(x)+\text{cos}^2(x)}{\text{sen}^2(x)}$

En revanche, on sait que le carré du sinus plus le carré du cosinus est égal à un grâce à l’identité trigonométrique fondamentale.

$\text{sen}^2(x)+\text{cos}^2(x)=1$

$\text{cotg}'(x)=-\cfrac{1}{\text{sen}^2(x)}$

Et nous avons ainsi obtenu la première formule de la dérivée de la cotangente. De même, la cosécante est l’inverse multiplicatif du sinus, donc la deuxième règle de la dérivée de la cotangente est également prouvée :

$\text{cotg}'(x)=-\text{sec}^2(x)$

Enfin, la troisième formule de la dérivée de cette fonction trigonométrique peut être prouvée en transformant la fraction de l’étape précédente en une somme de fractions :