Dans cet article, nous expliquons comment dériver l’arccotangente hyperbolique d’une fonction. De plus, vous pourrez voir des exemples résolus de la dérivée de l’arccotangente hyperbolique.
Formule de la dérivée de l’arccotangente hyperbolique
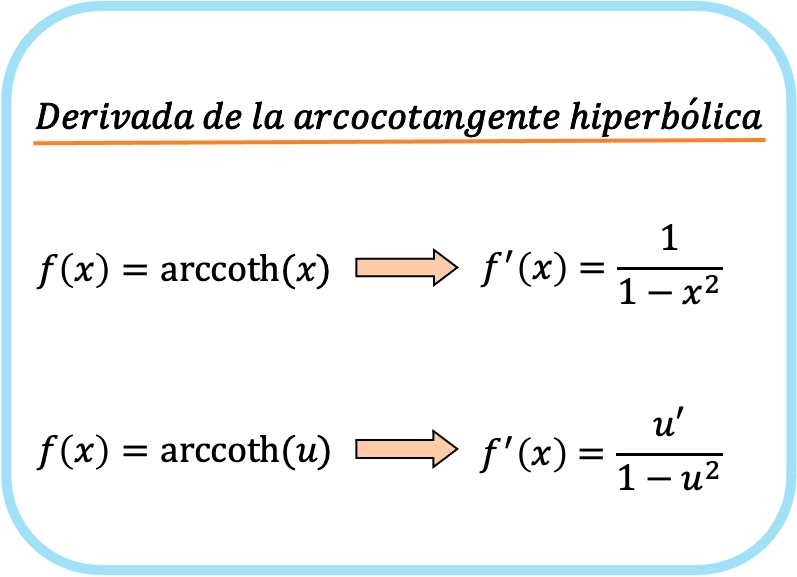
La dérivée de l’arccotangente hyperbolique de x est un sur un moins x au carré.
![]()
Par conséquent, la dérivée de l’arccotangente hyperbolique d’une fonction est égale au quotient de la dérivée de cette fonction divisé par un moins cette fonction au carré.
![]()
Notez que la deuxième formule est comme la première mais applique la règle de la chaîne, de sorte qu’elles pourraient en fait être considérées comme la même formule.
Il se peut que dans certains livres de mathématiques vous voyiez que la dérivée de ce type de fonction trigonométrique inverse est la suivante :
![]()
Cependant, si vous regardez attentivement, ce sont la même formule, la seule différence est que le numérateur et le dénominateur de la fraction ont été multipliés par -1.
Exemples de dérivée de l’arccotangente hyperbolique
Exemple 1
![]()
Dans l’argument arccotangente hyperbolique, nous avons une fonction différente de x, nous devons donc utiliser la formule de la règle de la chaîne pour la dériver :
![]()
La dérivée de 5x est 5, donc au numérateur de la fraction il faut mettre un 5 et au dénominateur un moins 5x élevé au carré :
![]()
Exemple 2
![]()
Pour résoudre la dérivée de cette fonction, nous devons appliquer la formule de la dérivée de l’arccotangente hyperbolique, qui est la suivante :
![]()
Dans ce cas, nous avons une fonction composée, puisqu’il y a une fonction exponentielle dans l’argument de la fonction trigonométrique. Nous devons donc utiliser la règle de la chaîne pour trouver la dérivée de la fonction entière :
![]()