Dans cet article, nous expliquons comment dériver l’arccosécante hyperbolique d’une fonction. Vous trouverez également des exemples travaillés de la dérivée de l’arccosécante hyperbolique.
Formule de la dérivée de l’arc cosécante hyperbolique
La dérivée de l’arc cosécante hyperbolique de x est égale à moins 1 divisé par le produit de x fois la racine de un plus x au carré.
![]()
Par conséquent, la dérivée de l’arc cosécante hyperbolique d’une fonction est moins la dérivée de ladite fonction divisée par le produit de la fonction par la racine de un plus la fonction au carré.
![]()
En résumé, la formule pour calculer la dérivée de la fonction arccosécante hyperbolique est la suivante :
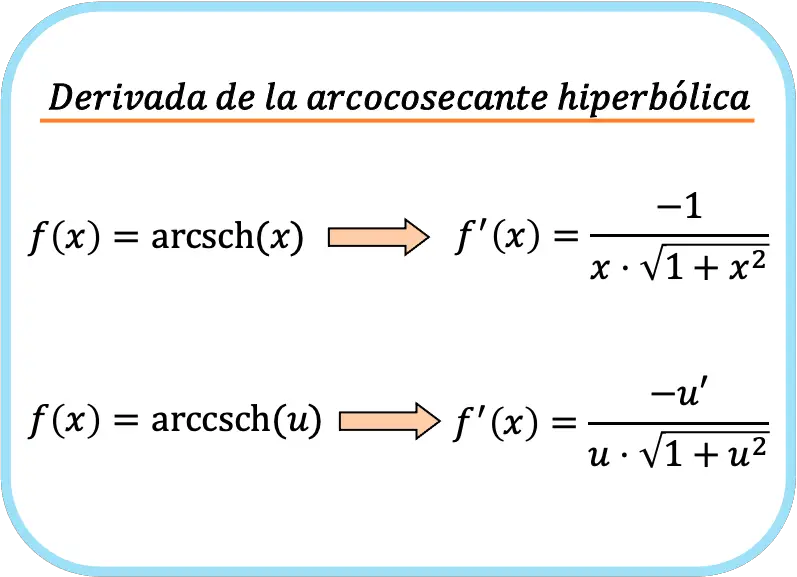
Bien que nous ayons mis deux formules, cela ne signifie pas qu’elles sont différentes. Si vous regardez attentivement, la deuxième formule est comme la première mais en appliquant la règle de la chaîne.
Exemples de la dérivée de l’arc cosécante hyperbolique
Étant donné la formule de la dérivée de l’arc cosécante hyperbolique, nous dériverons ensuite deux fonctions de ce type afin que vous puissiez voir comment cela se fait.
Exemple 1
![]()
Dans cet exercice, nous devons utiliser la formule de la dérivée de l’arc cosécante hyperbolique avec la règle de chaîne, car dans l’argument il y a une fonction différente de x :
![]()
Ainsi, pour trouver la dérivée, nous devons remplacer le u par 3x et le u’ par sa dérivée, qui est 3 :
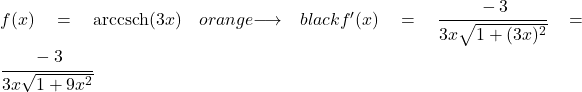
Exemple 2
![]()
Dans ce cas, nous avons une fonction polynomiale dans l’argument arccosécante hyperbolique, nous devons donc également utiliser la règle de chaîne pour la dériver :
![]()
Donc on met la dérivée de la fonction argument au numérateur de la fraction, et au dénominateur on change le u par la fonction polynomiale :
![Rendered by QuickLaTeX.com \begin{aligned}f(x)=\text{arccsch}(x^5-2x^3) \quad\color{orange}\bm{\longrightarrow}\quad\color{black}f'(x)&=\cfrac{-(5x^4-6x^2)}{(x^5-2x^3)\sqrt{1+(x^5-2x^3)^2}}\\[1.5ex] &=\cfrac{-5x^4+6x^2}{(x^5-2x^3)\sqrt{1+(x^5-2x^3)^2}}\end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-6257584425bd348ba75c7680d8ff6f70_l3.png)