Vous découvrirez ici comment dériver la fonction cosinus (formule). Vous pourrez voir des exemples de dérivées de fonctions cosinus et vous entraîner avec des exercices résolus étape par étape. De plus, nous vous montrons la démonstration de la formule, quelle est la dérivée seconde du cosinus et même la dérivée du cosinus inverse.
Quelle est la dérivée du cosinus ?
La dérivée de la fonction cosinus est la fonction sinus modifiée en signe. Autrement dit, la dérivée du cosinus de x est égale à moins le sinus de x.
S’il y a une fonction dans l’argument cosinus, la dérivée du cosinus est le produit de moins le sinus de cette fonction par la dérivée de la fonction.
La deuxième formule est équivalente à la première formule mais appliquant la règle de la chaîne. Ainsi, en résumé, la formule de la dérivée du cosinus est la suivante :
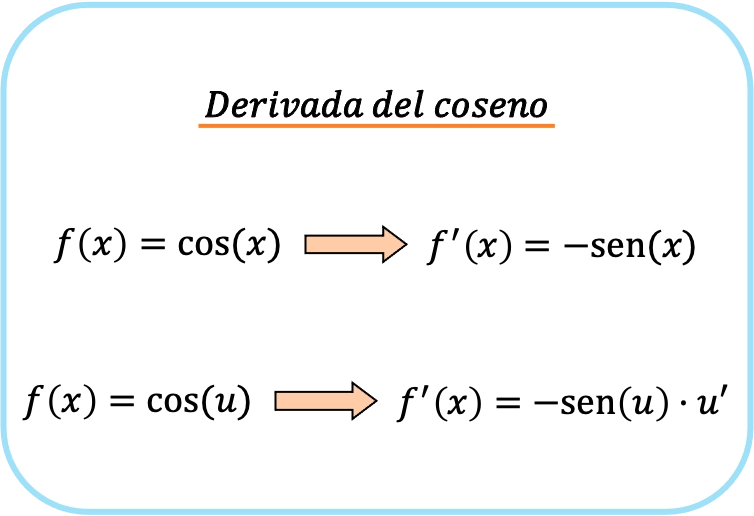
Exemples de dérivée du cosinus
Maintenant que nous savons ce qu’est la formule du cosinus, nous allons expliquer plusieurs exemples de ce type de dérivées trigonométriques afin que vous n’ayez aucun doute sur la façon de dériver la fonction cosinus.
Exemple 1 : Dérivée du cosinus de 2x
Dans l’argument cosinus, nous n’avons pas un seul x, mais plutôt une fonction plus complexe. Par conséquent, nous devons utiliser la formule suivante pour dériver le cosinus :
Puisque la dérivée de 2x est 2, la dérivée du cosinus de 2x sera moins le sinus de 2x multiplié par 2.
Exemple 2 : Dérivée du cosinus de x au carré
Comme dans l’exemple précédent, dans l’argument cosinus, nous avons une fonction différente de x, nous allons donc utiliser la règle de chaîne pour dériver le cosinus :
Alors, la dérivée de x 2 est 2x, par conséquent, la dérivée du cosinus de x élevé à la puissance 2 est :
Exemple 3 : Dérivée du cosinus au cube
La fonction cosinus dans cet exemple est composée d’une autre fonction, nous devons donc appliquer la formule suivante pour résoudre la dérivée :
Ainsi, en appliquant la formule, on arrive à la dérivée de la fonction :
![\begin{aligned}f'(x)&=3\text{cos}^2(2x^6-5x^3)\cdot \bigl(-\text{sen}(2x^6-5x^3)\bigr)\cdot (12x^5-15x^2)\\[2ex]&=-3\text{cos}^2(2x^6-5x^3)\cdot \text{sen}(2x^6-5x^3)\cdot (12x^5-15x^2)\end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-73284bcfb1d5647b2304e323e7fbaedf_l3.png "Rendered by QuickLaTeX.com")
➤ Afin de différencier cette fonction, vous devez également utiliser la formule de la dérivée d’une fonction potentielle .
Dérivée seconde du cosinus
Ensuite, nous verrons que la dérivée seconde du sinus peut être facilement calculée, grâce aux caractéristiques des fonctions trigonométriques.
➤ Remarque : pour comprendre ce qui suit, vous devez savoir quelle est la dérivée du sinus .
La dérivée seconde du cosinus de x est moins le cosinus de x. Cela peut paraître étrange, mais mathématiquement c’est comme ça. En effet, la dérivée du sinus est le cosinus et, par conséquent, en différenciant deux fois le cosinus de x, le cosinus est à nouveau obtenu mais avec un signe modifié.
![\begin{array}{c}f(x)=\text{cos}(x)\\[1.5ex] \quad\color{orange}\bm{\downarrow}\quad\color{black} \\[1.5ex] f'(x)=-\text{sen}(x)\\[2ex] \quad\color{orange}\bm{\downarrow}\quad\color{black} \\[1.5ex] f''(x)=-\text{cos}(x)\end{array}](https://mathority.org/wp-content/ql-cache/quicklatex.com-d0d9dda8a4031c367120b1f950da4391_l3.png "Rendered by QuickLaTeX.com")
Cette propriété change si l’argument cosinus n’est pas x, puisque dans ce cas nous faisons glisser le terme de la règle de chaîne :
![\begin{array}{c}f(x)=\text{cos}(u)\\[1.5ex] \quad\color{orange}\bm{\downarrow}\quad\color{black} \\[1.5ex] f'(x)=-\text{sen}(u)\cdot u' \\[1.5ex] \quad\color{orange}\bm{\downarrow}\quad\color{black} \\[1.5ex] f''(x)=-\text{cos}(u)\cdot u'^2 -\text{sen}(u)\cdot u'' \end{array}](https://mathority.org/wp-content/ql-cache/quicklatex.com-83d86bd6508f06b0723153b3b9254c1f_l3.png "Rendered by QuickLaTeX.com")
Dérivée du cosinus inverse
Toutes les fonctions trigonométriques ont une fonction inverse et en tant que telle, la fonction cosinus peut également être inversée. De même, le cosinus inverse est différentiable.
La dérivée du cosinus inverse d’une fonction est moins la dérivée de la fonction divisée par la racine carrée de un moins le carré de ladite fonction.
N’oubliez pas que le cosinus inverse est également appelé arccosinus.
Par exemple, la dérivée du cosinus inverse de 3x est :
Exercices résolus sur la dérivée du cosinus
Calculez la dérivée des fonctions cosinus suivantes :
![\begin{aligned}\text{F) }\displaystyle f'(x)&=-9\text{sen}\left(\frac{e^x}{5x}\right)\cdot \frac{e^x\cdot 5x-e^x\cdot 5}{(5x)^2}\\[2ex]&=-9\text{sen}\left(\frac{e^x}{5x}\right)\cdot \frac{5e^x(x-1)}{25x^2}\\[2ex]&=-9\text{sen}\left(\frac{e^x}{5x}\right)\cdot \frac{e^x(x-1)}{5x^2}\end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-9f4645fb77435daec6f696cffbd54884_l3.png "Rendered by QuickLaTeX.com")
Preuve de la dérivée du cosinus
Enfin, nous allons démontrer mathématiquement la formule de la dérivée du cosinus de x. Pour ce faire, nous utiliserons la définition de la dérivée, qui correspond à la limite suivante :
Nous allons faire la preuve du cosinus, donc la fonction est cos(x) :
Nous ne pouvons pas résoudre cette limite par substitution, car nous aboutirions à l’indétermination. Cependant, on peut exprimer le cosinus d’une somme d’une autre manière en appliquant l’identité trigonométrique suivante :
L’étape suivante consiste à séparer la fraction en deux fractions et à prendre le facteur commun du cosinus :
![\displaystyle f'(x)=\lim_{h \to 0}\left[\frac{\text{cos}(x)\bigl(\text{cos}(h)-1\bigr)}{h}-\frac{\text{sen}(x)\text{sen}(h)}{h}\right]](https://mathority.org/wp-content/ql-cache/quicklatex.com-c7c1cd89cf290b01d7d72fc8084f6529_l3.png "Rendered by QuickLaTeX.com")
La limite d’une soustraction est égale à la soustraction des limites, donc :
Le cosinus de x et le sinus de x ne dépendent pas de h, nous pouvons donc les extraire hors limites :
En utilisant le calcul des limites par équivalents infinitésimaux, nous concluons que la première limite est 0 et la deuxième limite est 1. Donc :
Et nous avons déjà atteint la formule de la dérivée de la fonction cosinus, donc l’égalité est prouvée.