Limite d'une fonction -

Vous découvrirez ici ce que sont les limites de fonction et comment tous les types de limites sont calculés. Et non seulement vous verrez ce que signifie la limite d’une fonction, mais nous vous expliquerons également à quoi elles servent. De plus, vous pouvez vous entraîner avec des exercices étape par étape sur les limites des fonctions.

Quelle est la limite d’une fonction ?

En mathématiques, la limite d’une fonction en un point est la valeur à laquelle la fonction se rapproche à mesure que x s’approche de ce point.

La limite de la fonction f(x) au point x=a est représentée à l’aide de la notation suivante :

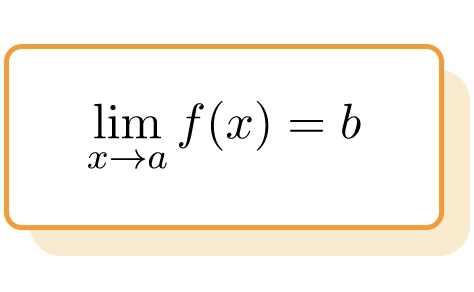
L’expression précédente signifie que la limite de la fonction f(x) lorsque x tend vers

$a$ est égal à b.

Pour finir de comprendre ce que signifie la limite d’une fonction, nous allons trouver la limite suivante :

$\displaystyle\lim_{x\to 2}(x^2-4x+5)= \ \color{red}\bm{?}$

Pour voir de quelle valeur se rapproche la fonction lorsque x tend vers 2, on peut calculer des images de la fonction de points de plus en plus proches de x=2 :

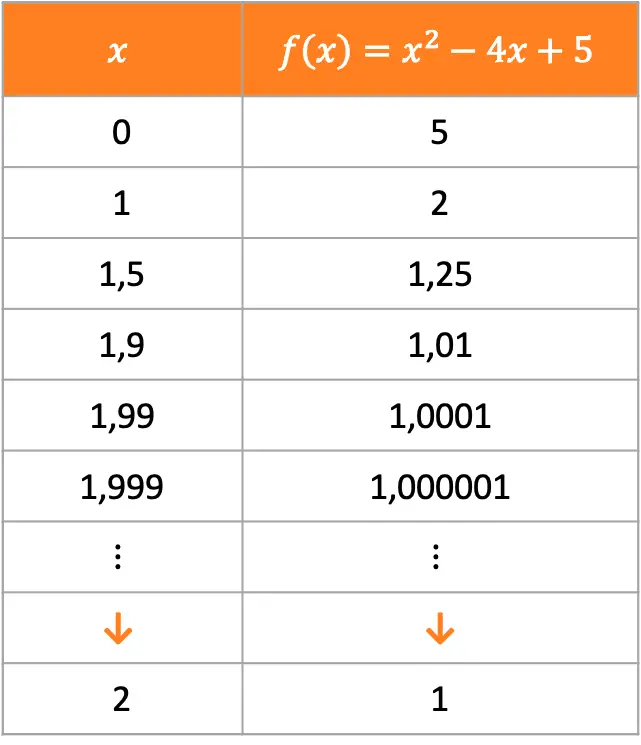
limite d'une fonction en un point à gauche

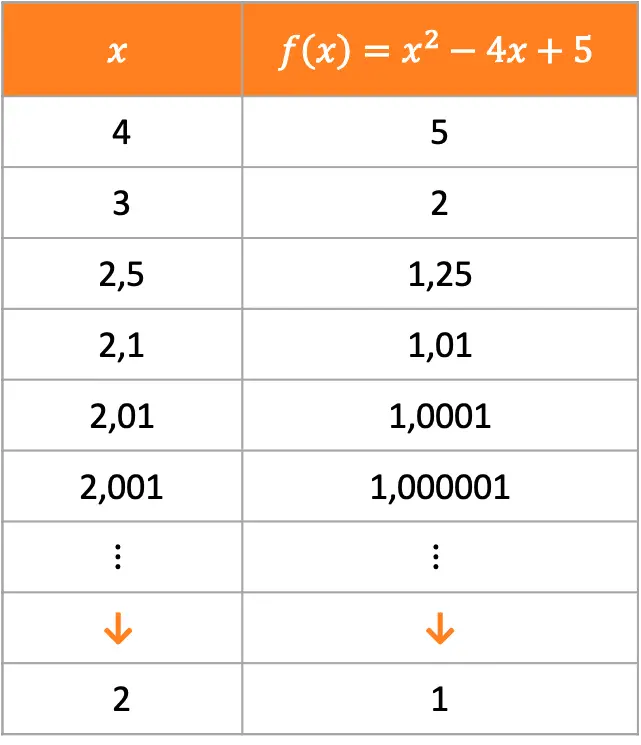
limite d'une fonction en un point à droite

Comme vous pouvez le voir dans les deux tableaux précédents, à mesure que l’on prend des valeurs plus proches de x=2, la fonction se rapproche de 1. Par conséquent, la limite de la fonction lorsque x tend vers 2 est 1.

$\displaystyle\lim_{x\to 2}(x^2-4x+5)= \color{red}\bm{1}$

Ci-dessous, vous pouvez voir la fonction représentée graphiquement. Comme vous pouvez le voir, la fonction tend vers 1 lorsque x tend vers 2.

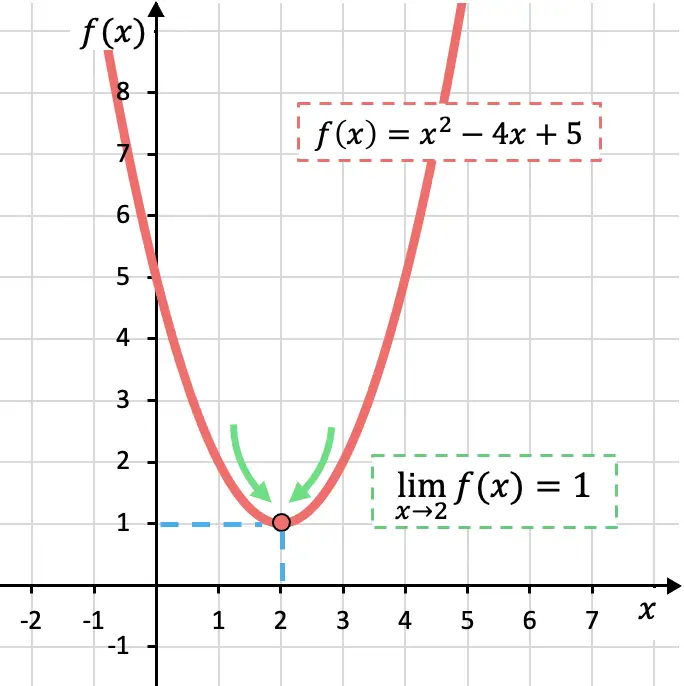
Remarquez sur le graphique que la fonction s’approche de la même valeur, que l’on s’approche par la gauche ou par la droite. Ci-dessous, nous approfondirons ce concept de limites.

Comment calculer la limite d’une fonction

Pour calculer la limite d’une fonction en un point, nous devons simplement substituer la valeur de ce point dans la fonction.

Par exemple, si l’on veut résoudre la limite lorsque x tend vers 3 de la fonction suivante, il faut remplacer le x de la fonction par 3 :

$\begin{array}{l}\displaystyle\lim_{x \to \color{blue}\bm{3}\color{black}} \left(x^2+5x-7\right)=\\[3ex]=\color{blue}\bm{3}\color{black}^2+5\cdot \color{blue}\bm{3}\color{black}-7=\\[3ex]=9+15-7=17\end{array}$

Autres exemples de calculs de limites de fonction :

$\displaystyle \lim_{x \to 1} \left(4x-1 \right) = 4\cdot 1- 1 =\bm{3}$

$\displaystyle \lim_{x \to -2} \left(x^2-3x +1\right) =(-2)^2-3(-2) + 1=\bm{11}$

$\displaystyle \lim_{x \to 3} \cfrac{2x}{x-2} = \cfrac{2\cdot 3}{3-2}= \cfrac{6}{1} =\bm{6}$

$\displaystyle \lim_{x \to 0} e^x = e^0 =\bm{1}$

$\displaystyle \lim_{x \to -1} \cfrac{x+1}{x-1} = \cfrac{-1+1}{-1-1}= \cfrac{0}{-2} =\bm{0}$

Limites latérales d’une fonction

Une fois que nous avons vu la définition de la limite d’une fonction, nous allons analyser la notion de limites latérales. Il existe deux types de limites latérales : la limite latérale à gauche et la limite latérale à droite.

La limite latérale de la fonction à gauche est exprimée par un signe moins au point où la limite est analysée et, par contre, la limite latérale à droite est indiquée par le signe plus.

Limite latérale à gauche

$\displaystyle\lim_{x\to a^{\color{orange}\bm{-}\color{black}}}f(x)$

Limite latérale à droite

$\displaystyle\lim_{x\to a^{\color{orange}\bm{+}\color{black}}}f(x)$

Regardez l’exemple suivant pour mieux comprendre la signification des limites latérales :

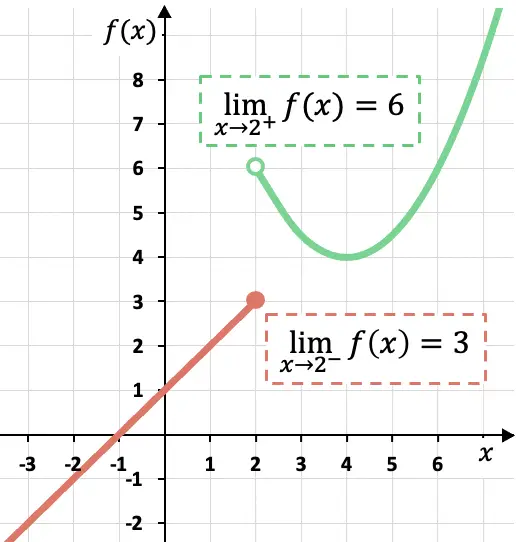
Comme vous pouvez le voir sur la représentation graphique de cette fonction par morceaux, les limites latérales dépendent du côté sur lequel elles sont calculées.

Dans ce cas, la fonction tend vers 3 à mesure que x s’approche de 2 par la gauche, puisque la fonction prend des valeurs de plus en plus proches de 3 à mesure que x s’approche de x=2 par sa gauche.

En revanche, la limite latérale de la fonction en x=2 à droite est 6. Car si l’on s’approche du point x=2 par sa droite, la fonction prend des valeurs de plus en plus proches de f(x) =6.

Limites latérales égales

Nous venons de voir un exemple dans lequel les limites latérales d’une fonction sont différentes, mais… que se passe-t-il si les limites latérales sont égales ?

Si les deux limites latérales d’une fonction en un point existent et sont égales , la limite de la fonction en ce point existe et le résultat de la limite est la valeur des limites latérales.

Autrement dit, pour que la limite d’une fonction existe en un point, la condition suivante doit être remplie :

$\displaystyle\lim_{x\to a^-}f(x)=\lim_{x\to a^+}f(x)=L \ \iff \ \lim_{x\to a}f(x)=L$

Par conséquent, si les limites latérales d’une fonction en un point sont différentes, la limite de la fonction en ce point n’existe pas.

Résolvons un exemple pour bien comprendre le concept de limites latérales :

Les limites latérales au point x=-2 de la fonction représentée graphiquement coïncident, puisque la valeur de la fonction tend vers 3 que l’on s’approche de x=-2 par la gauche ou par la droite. Par conséquent, la limite de la fonction à x=-2 est égale à 3.

$\displaystyle\lim_{x\to -2^-}f(x)=\lim_{x\to -2^+}f(x)=3 \ \longrightarrow \ \lim_{x\to -2}f(x)=3$

Par contre, au point x=4 les limites latérales sont différentes, puisqu’à gauche la fonction se rapproche de f(x)=3 mais à droite la fonction se rapproche de f(x)=2. La limite de la fonction n’existe donc pas à ce stade.

$\displaystyle\lim_{x\to 4^-}f(x)=3 \neq \lim_{x\to 4^+}f(x)=2 \ \longrightarrow \ \cancel{\exists} \ \lim_{x\to 4}f(x)$

Nous venons de voir comment déterminer la limite latérale d’une fonction à partir d’un graphique, cependant, calculer numériquement une limite latérale est plus compliqué. C’est pourquoi nous vous recommandons de voir comment calculer les limites latérales.

Limite d’une fonction par morceaux

Le calcul de la limite d’une fonction par morceaux en un point dépend du fait que ce point soit le point de rupture ou non :

Si vous souhaitez calculer la limite d’une fonction par morceaux en un point qui n’est pas le point de rupture , le calcul de la limite se fait sur la partie de la fonction qui correspond à ce point.
Si vous souhaitez calculer la limite d’une fonction par morceaux au point de rupture , vous devez calculer les limites latérales au point de rupture :
Si les deux limites latérales coïncident avec la même valeur, c’est la valeur de la limite de la fonction au point de rupture.
Si les deux limites latérales ne coïncident pas, alors la limite de la fonction au point de rupture n’existe pas.

Regardons un exemple pour mieux comprendre comment la limite d’une fonction par morceaux est calculée :

Calculez les limites aux points x=1 et x=3 de la fonction par morceaux suivante :

$\displaystyle f(x)= \left\{ \begin{array}{lcl} x+3 & \text{si} & x<3 \\[2ex] 2x & \text{si} & x\ge 3 \end{array} \right.$

Pour calculer la limite de la fonction lorsque x tend vers 1, il faut utiliser la première fonction, puisque x=1 appartient à l’intervalle x<3. Pourtant:

$\displaystyle\lim_{x \to 1} f(x) = \lim_{x \to 1} \left(x+3 \right)=1+3 =\bm{4}$

Ainsi, la limite de la fonction lorsque x tend vers 1 est 4.

Au lieu de cela, x=3 est le point de rupture de la fonction . Parce qu’à ce stade, la fonction change de section.

Alors, puisque x=3 est le point de rupture de la fonction, pour trouver la limite de la fonction lorsque x tend vers 3 il faut calculer ses limites latérales :

$\displaystyle \lim_{x \to 3^{-}} f(x) = \lim_{x \to 3} \left(x +3\right)=3+3= \bm{6}$

$\displaystyle \lim_{x \to 3^{+}} f(x)= \lim_{x \to 3} 2x = 2\cdot3= \bm{6}$

Donc la limite de

$f(x)$ Lorsque x tend vers 3 en partant de la gauche, c’est 6 . et la limite de $f(x)$ lorsque x tend vers 3 par la droite, il vaut également 6. Par conséquent, puisque les deux limites latérales sont égales, la limite de la fonction lorsque x tend vers 3 est 6 :

$\displaystyle \lim_{x \to 3^-} f(x) = \lim_{x \to 3^+} f(x) = 6 \quad \bm{\longrightarrow} \quad \lim_{x \to 3} f(x) = \bm{6}$

Nous allons maintenant voir un exemple où les limites latérales au point de rupture ne coïncident pas :

Calculez la limite lorsque x s’approche de 4 de la fonction par morceaux suivante :

$\displaystyle f(x)= \left\{ \begin{array}{lcl} -x-1 & \text{si} & x\le4 \\[2ex] 2x^2 & \text{si} & x>4 \end{array} \right.$

x=4 est le point de rupture de la fonction, puisqu’à ce stade la fonction change de section. Il faut donc calculer les deux limites latérales de la fonction en ce point :

$\displaystyle \lim_{x \to 4^{-}} f(x) = \lim_{x \to 4}} \left(-x -1\right)=-4-1= \bm{-5}$

$\displaystyle \lim_{x \to 4^{+}} f(x)= \lim_{x \to 4}} 2x^2 = 2\cdot 4^2=\bm{32}$

Donc la limite de

$f(x)$ Lorsque x tend vers 4 en partant de la gauche, c’est -5 . et la limite de $f(x)$ lorsque x tend vers 5 à droite, il vaut 32. Par conséquent, puisque les deux limites latérales ne coïncident pas, la limite de la fonction lorsque x tend vers 4 n’existe pas :

$\displaystyle \lim_{x \to 4^-} f(x) \neq \lim_{x \to 4^+} f(x) \quad \bm{\longrightarrow} \quad \cancel{\exists} \lim_{x \to 4} f(x)$

Limite d’une fonction à l’infini

La limite d’une fonction lorsque x tend vers l’infini , qu’elle soit positive ou négative, peut être une valeur réelle, plus l’infini, moins l’infini ou inexistante.

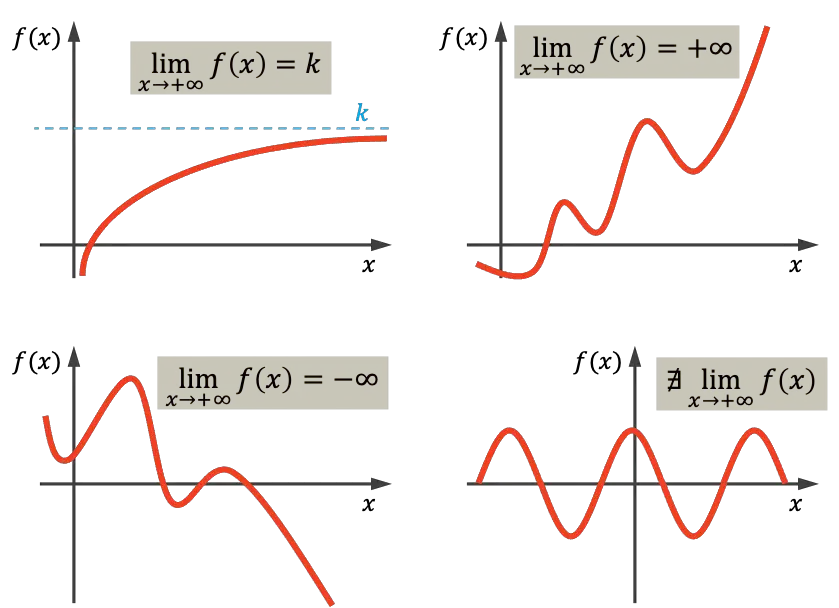
Comme vous pouvez le voir sur le premier graphique, la fonction représentée tend vers la valeur réelle k vers l’infini, car elle se rapproche de k à mesure que x grandit. La fonction en haut à droite tend vers l’infini lorsque x tend vers l’infini, car elle croît indéfiniment à mesure que x augmente en valeur. En revanche, le graphique en bas à gauche diminue sans s’arrêter et tend donc vers moins l’infini. Enfin, la dernière fonction est périodique et ne tend vers aucune valeur, il n’y a donc pas de limite à l’infini dans ce cas.

Résoudre ce type de limites n’est pas chose aisée, puisqu’une procédure préalable doit être appliquée. Et même selon la limite à l’infini, cette procédure varie. Pour voir comment les limites sont résolues à l’infini, cliquez sur le lien suivant :

➤ Voir : comment résoudre les limites à l’infini

Limites indéterminées

Les indéterminations , également appelées formes indéterminées , sont des expressions mathématiques qui apparaissent dans le calcul des limites de fonctions dont le résultat n’est pas défini.

Les différents types d’indéterminations sont les suivants :

Indétermination infini moins l’infini (∞-∞)
Nombre d’indétermination entre zéro (k/∞)
Zéro indétermination entre zéro (0/0)
Indétermination infinie entre l’infini (∞/∞)
Indétermination 1 élevée à l’infini (1 ^∞ )
Indétermination zéro élevée à zéro (0 ⁰ )
Zéro indétermination pour l’infini (0·∞)
Indétermination zéro élevée à l’infini (0 ^∞ )
Indétermination infinie portée à zéro (∞ ⁰ )

Autrement dit, lorsque dans le calcul d’une limite nous obtenons une indétermination des précédentes, cela ne signifie pas que la limite n’existe pas ou qu’elle ne peut pas être résolue, mais plutôt que nous devrons apporter des modifications à la fonction dans afin de trouver la solution de la limite.

Dans le lien suivant, vous pouvez voir l’explication sur la façon de résoudre tous les types d’indéterminations :

➤ Voir : comment résoudre les indéterminations

A quoi servent les limites de fonction ?

Si vous êtes arrivé jusqu’ici, vous savez sûrement déjà ce que signifie la limite d’une fonction et quand la limite d’une fonction existe. Mais… à quoi sert la limite d’une fonction ?

Eh bien, la principale application des limites des fonctions est d’étudier la continuité d’une fonction, ou en d’autres termes, calculer la limite d’une fonction en un point sert à savoir si ladite fonction est continue en ce point ou non. Vous pouvez voir comment cela se fait dans le lien suivant :

➤ Voir : continuité d’une fonction

D’un autre côté, les limites servent également à calculer les asymptotes d’une fonction, qu’il s’agisse d’une asymptote verticale, d’une asymptote horizontale ou d’une asymptote oblique. Si vous êtes plus intéressé, vous pouvez rechercher sur notre site Web comment calculer les asymptotes d’une fonction.

Exercices résolus sur les limites des fonctions

Ci-dessous, nous avons préparé 37 exercices résolus étape par étape de tous les types de limites de fonctions que nous avons vu ci-dessus. Vous pouvez essayer de les faire, puis vérifier la solution.

N’oubliez pas que vous pouvez nous poser toutes vos questions sur la résolution des limites ci-dessous dans les commentaires !

Exercices de limites simples

Exercice 1

Résolvez les limites de fonction suivantes :

$\text{A)}\ \displaystyle\lim_{x\to 1}(x+3)$

$\text{B)}\ \displaystyle\lim_{x\to 2}(-2x+5)$

$\text{C)}\ \displaystyle\lim_{x\to 0}(-7x-2)$

$\text{D)}\ \displaystyle\lim_{x\to -1}(2x^2-3x+6)$

Voir la solution

Pour calculer les limites, nous substituons la valeur de x dans la fonction et effectuons les opérations :

$\text{A)}\ \displaystyle \lim_{x \to 1} (x+3)=1 + 3 = \bm{4}$

$\text{B)}\ \displaystyle \lim_{x \to 2} (-2x+5) = -2\cdot2+5= -4 + 5 = \bm{1}$

$\text{C)}\ \displaystyle \lim_{x \to 0} (-7x-2) = -7\cdot0-2 = \bm{-2}$

$\text{D)}\ \displaystyle \lim_{x \to -1} (2x^2-3x+6) = 2(-1)^2-3\cdot (-1)+6=\bm{11}$

Exercice 2

Calculez les limites suivantes des fonctions :

$\text{A)}\ \displaystyle \lim_{x \to 3} \cfrac{2x+1}{x^2-2}$

$\text{B)}\ \displaystyle\lim_{x \to 2} \sqrt{2x^2+6x-4}$

$\text{C)}\ \displaystyle\lim_{x \to -4} \left(\frac{3x}{2} +5 \right)$

$\text{D)}\ \displaystyle\lim_{x \to 0} e^{2x}$

$\text{E)}\ \displaystyle\lim_{x \to 0} \left( 1 + \cos x \right)$

Voir la solution

Bien que les calculs de cet exercice soient un peu plus compliqués, ces limites peuvent également être résolues par substitution :

$\text{A)}\ \displaystyle \lim_{x \to 3} \cfrac{2x+1}{x^2-2}= \cfrac{2\cdot 3+1}{3^2-2} = \cfrac{6+1}{9-2} = \cfrac{7}{7} = \bm{1}$

$\text{B)}\ \displaystyle\lim_{x \to 2} \sqrt{2x^2+6x-4}=\sqrt{2(2)^2+6(2)-4}=\sqrt{16} = \bm{4}$

$\text{C)}\ \displaystyle\lim_{x \to -4} \left(\frac{3x}{2} +5 \right)=\frac{3\cdot(-4)}{2} +5= -6 +5 = \bm{-1}$

$\text{D)}\ \displaystyle\lim_{x \to 0} e^{2x} = e^{2\cdot 0} = e^{0}=\bm{1}$

$\text{E)}\ \displaystyle\lim_{x \to 0} \left( 1 + \cos x \right)= 1 + \cos 0 = 1 + 1 = \bm{2}$

Exercices de limites latérales des fonctions

Exercice 3

Trouvez les limites latérales de la fonction par morceaux suivante représentée graphiquement aux points où sa définition change (x=-2 et x=4).

Voir la solution

Les limites latérales ne coïncident pas au point x=-2, à gauche la fonction se rapproche de f(x)=5 et, par contre, à droite la fonction est constante et vaut 3.

$\displaystyle\lim_{x\to -2^-}f(x)=5$

$\displaystyle\lim_{x\to -2^+}f(x)=3$

Les limites latérales sont également différentes lorsque x tend vers 4. La fonction par morceaux tend vers 3 à gauche, mais à droite elle tend vers -2.

$\displaystyle\lim_{x\to 4^-}f(x)=3$

$\displaystyle\lim_{x\to 4^+}f(x)=-2$

Exercice 4

À partir du graphique ci-dessous, déterminez si la limite lorsque x s’approche de 3 de la fonction par morceaux suivante existe et, si oui, quelle est sa valeur.

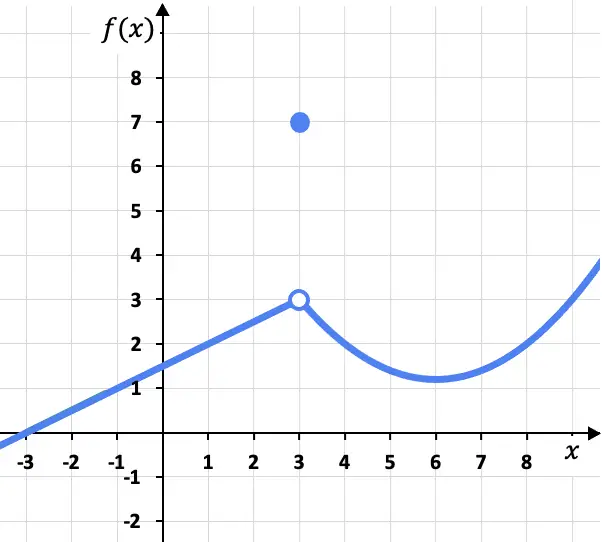
limites latérales d'une fonction définie par morceaux

Voir la solution

Dans ce problème, les limites latérales au point x=3 depuis la gauche et depuis la droite sont identiques, puisque la fonction se rapproche de la même valeur (f(x)=3) qu’on l’approche par le côté gauche ou par la droite côté. son côté droit :

$\displaystyle\lim_{x\to 3^-}f(x)=3$

$\displaystyle\lim_{x\to 3^+}f(x)=3$

Par conséquent, selon la définition mathématique d’une limite, la limite de la fonction lorsque x tend vers 3 est égale à 3, car les deux limites latérales en ce même point coïncident dans cette valeur :

$\displaystyle\lim_{x\to 3^-}f(x)=\lim_{x\to 3^+}f(x)=3 \ \longrightarrow \ \lim_{x\to 3}f(x)=3$

Bien que la limite de la fonction en x=3 soit 3, nous devons tenir compte du fait que la fonction en ce point n’est pas 3, mais f(3)=7. Comme nous le verrons plus tard, cela signifie que la fonction n’est pas continue en x=3, mais présente plutôt une discontinuité évitable.

Exercice 5

Calculez les limites latérales de la fonction rationnelle suivante au point x=4.

$f(x)=\cfrac{-2x+3}{x-4}$

Voir la solution

Pour calculer la limite lorsque x tend vers 4 en partant de la gauche on prend une valeur inférieure à 4 mais très proche, par exemple 3,999 :

$\displaystyle\lim_{x\to 4^-}\frac{-2x+3}{x-4}=\frac{-2\cdot 3,999+3}{3,999-4}=\frac{-4,998}{-0}=+\infty$

Ainsi, la limite latérale lorsque x s’approche de 4 depuis la gauche est plus infinie.

Et pour résoudre la limite lorsque x tend vers 4 depuis la droite, on évalue la fonction à une valeur supérieure à 4 mais très proche de celle-ci, par exemple 4,001 :

$\displaystyle\lim_{x\to 4^+}\frac{-2x+3}{x-4}=\frac{-2\cdot 4,001+3}{4,001-4}=\frac{-5,002}{+0}=-\infty$

Ainsi, la limite latérale lorsque x tend vers 4 à droite est plus infinie.

Exercice 6

Calculez la limite, si elle existe, de la fonction par morceaux suivante au point x=2 :

$\displaystyle f(x)= \left\{ \begin{array}{lcl} x^2-3 & \text{si} & x \leq 2 \\[2ex]\displaystyle \frac{-3x+5}{x-3} & \text{si} & x>2 \end{array} \right.$

Voir la solution

Dans ce cas, l’énoncé du problème nous demande de calculer la limite où la fonction par morceaux change d’expression, nous devons donc trouver la limite latérale à gauche en utilisant la première expression et la limite latérale à droite en utilisant la deuxième expression.

$\displaystyle\lim_{x\to 2^-}f(x)=\lim_{x\to 2^-}(x^2-3)=2^2-3=1$

$\displaystyle\lim_{x\to 2^+}f(x)=\lim_{x\to 2^+}\frac{-3x+5}{x-3}=\frac{-3\cdot 2+5}{2-3}=\frac{-1}{-1}=1$

La limite de la fonction en x=2 à gauche coïncide avec la limite de la fonction à droite, donc la limite de la fonction existe et est égale à 1 :

$\displaystyle\lim_{x\to 2^-}f(x)=\lim_{x\to 2^+}f(x)=1 \ \longrightarrow \ \lim_{x\to 2}f(x)=1$

Exercice 7

Calculez les limites de la fonction suivante définie par morceaux aux points x=-1, x=1 et x=2 :

$\displaystyle f(x)= \left\{ \begin{array}{lcl} x^3+x^2+1 & \text{si}&x\le1\\[3ex] \displaystyle \frac{x^2-4}{-3x+4} & \text{si} & x>1 \end{array} \right.$

Voir la solution

a) Pour calculer la limite de la fonction définie par segments lorsque x tend vers -1 il faut utiliser la première fonction, car x=-1 appartient à l’intervalle x≤1. Pourtant:

$\displaystyle \lim_{x \to -1} f(x) = \lim_{x \to -1}(x^3+x^2+1)= (-1)^3+(-1)^2+1=\bm{1}$

b) x=1 est le point de changement de définition de la fonction par morceaux, nous calculons donc les limites latérales :

$\displaystyle \lim_{x \to 1^{-}} f(x) = \lim_{x \to 1}(x^3+x^2+1)=1^3+1^2+1=3$

$\displaystyle \lim_{x \to 1^{+}} f(x)=\lim_{x \to 1} \cfrac{x^2-4}{-3x+4}=\cfrac{1^2-4}{-3\cdot1+4}=\cfrac{-3}{1}= -3$

Puisque les deux limites latérales ne donnent pas le même résultat, la limite de la fonction lorsque x tend vers 1 n’existe pas :

$\displaystyle \lim_{x \to 1^-} f(x) \neq \lim_{x \to 1^+} f(x)\ \bm{\longrightarrow} \ \cancel{\exists} \lim_{x \to 1} f(x)$

c) Enfin, pour trouver la limite de la fonction lorsque x tend vers 2, il faut utiliser la deuxième fonction car x=2 appartient à l’intervalle x>1. Pourtant:

$\displaystyle \lim_{x \to 2} f(x) = \lim_{x \to 2} \cfrac{x^2-4}{-3x+4} =\cfrac{2^2-4}{-3\cdot 2+4}= \cfrac{0}{-2}=\bm{0}$

Exercices sur les limites des fonctions à l’infini

Exercice 8

Trouvez les limites suivantes de la fonction représentée par le graphique suivant :

$\displaystyle\lim_{x\to -\infty}f(x)$

$\displaystyle\lim_{x\to +\infty}f(x)$

$\displaystyle\lim_{x\to -1^-}f(x)$

$\displaystyle\lim_{x\to -1^+}f(x)$

$\displaystyle\lim_{x\to 1^-}f(x)$

$\displaystyle\lim_{x\to 1^+}f(x)$

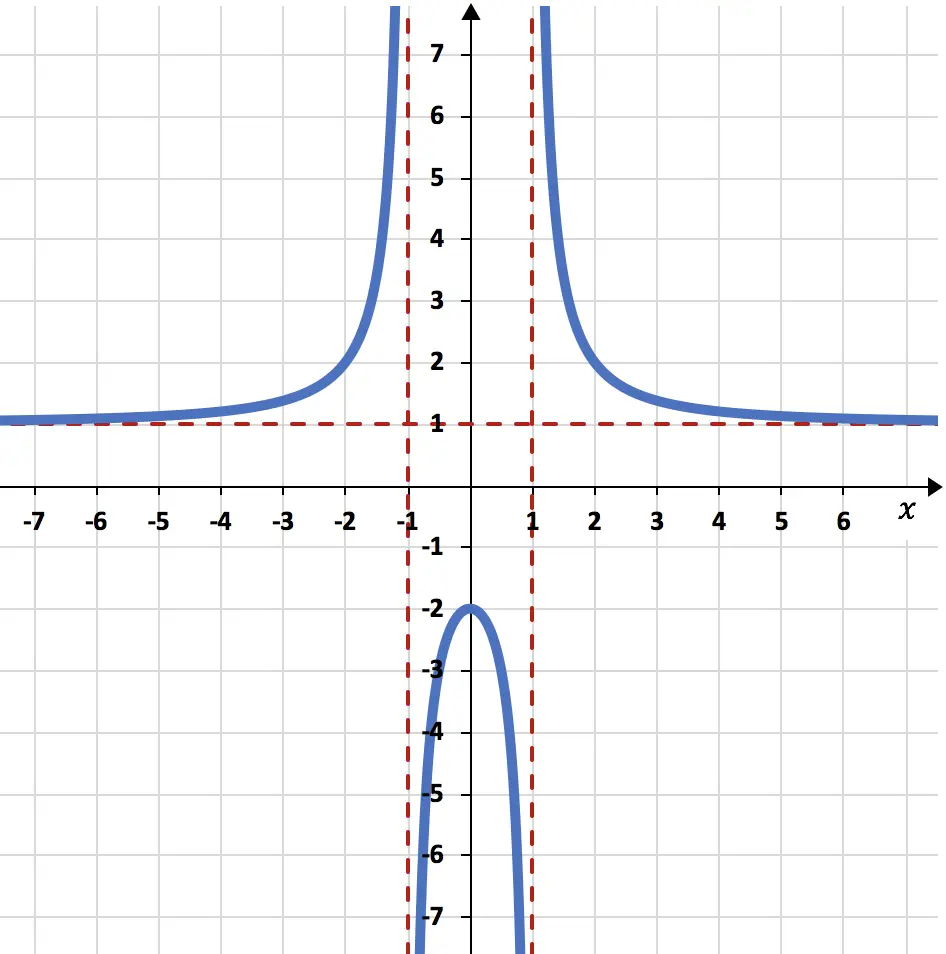
limites à l'infini à partir de la représentation d'une fonction

Voir la solution

La limite de la fonction lorsque x tend vers moins l’infini et plus l’infini donne 1 :

$\displaystyle\lim_{x\to -\infty}f(x)=1$

$\displaystyle\lim_{x\to +\infty}f(x)=1$

Les limites latérales de la fonction à gauche et à droite au point x=-1 sont respectivement plus l’infini et moins l’infini :

$\displaystyle\lim_{x\to -1^-}f(x)=+\infty$

$\displaystyle\lim_{x\to -1^+}f(x)=-\infty$

Enfin, les limites latérales de la fonction lorsque x tend vers 1 valent moins l’infini et plus l’infini :

$\displaystyle\lim_{x\to 1^-}f(x)=-\infty$

$\displaystyle\lim_{x\to 1^+}f(x)=+\infty$

Exercice 9

Résolvez la limite lorsque x tend vers plus l’infini de la fonction suivante :

$\displaystyle \lim_{x \to +\infty} (x^2+4x+1)$

Voir la solution

Pour résoudre la limite à l’infini, nous devons remplacer x par l’infini dans le terme du plus haut degré du polynôme :

$\displaystyle \lim_{x \to +\infty} (x^2+4x+1) = (+\infty)^2= \bm{+\infty}$

Exercice 10

Calculez la limite à l’infini de la fonction polynomiale suivante :

$\displaystyle \lim_{x \to +\infty} (-3x^2+8x+5)$

Voir la solution

Pour résoudre la limite à l’infini, nous remplaçons x par l’infini dans le terme du plus haut degré du polynôme et effectuons les calculs :

$\displaystyle \lim_{x \to +\infty} (-3x^2+8x+5) = -3(+\infty)^2= -3\cdot (+\infty) = \bm{-\infty}$

Exercice 11

Résolvez la limite au moins infinie de la fonction polynomiale suivante :

$\displaystyle \lim_{x \to -\infty} (6x^2-3x-4)$

Voir la solution

Pour calculer la limite à l’infini, nous remplaçons x par moins l’infini dans le terme du plus haut degré du polynôme et évaluons la fonction :

$\displaystyle \lim_{x \to -\infty} (6x^2-3x-4) = 6(-\infty)^2= 6\cdot (+\infty) = \bm{+\infty}$

Puisque moins l’infini est au carré, le signe de l’infini devient positif.

Exercice 12

Trouver la limite à l’infini de la fonction rationnelle suivante :

$\displaystyle \lim_{x \to +\infty}\frac{7}{2x-5}$

Voir la solution

Pour déterminer la limite à l’infini, nous remplaçons x par plus l’infini au terme du plus haut degré du numérateur et du dénominateur de la fraction :

$\displaystyle \lim_{x \to +\infty}\frac{7}{2x-5} = \cfrac{7}{2\cdot(+\infty)}=\frac{7}{+\infty}=\bm{0}$

N’oubliez pas que tout nombre divisé par plus ou moins l’infini est égal à 0.

Exercice 13

Résolvez la limite suivante à l’infini :

$\displaystyle \lim_{x \to -\infty} (-x^3+x^2+5x)$

Voir la solution

Pour calculer la limite lorsque x tend vers ±∞ d’une fonction il suffit de regarder le monôme du plus haut degré de la fonction :

$\displaystyle \lim_{x \to -\infty} (-x^3+x^2+5x) = -(-\infty)^3= -(-\infty)= \bm{+\infty}$

Exercice 14

Calculez la limite de la fonction suivante lorsque x s’approche de moins l’infini :

$\displaystyle \lim_{x \to -\infty} (-4x^2+4)$

Voir la solution

Dans ce cas, il suffit de substituer l’infini au terme quadratique :

$\displaystyle \lim_{x \to -\infty} (-4x^2+4) = -4(-\infty)^2= -4\cdot (+\infty) = \bm{-\infty}$

Exercice 15

Trouvez la limite de la fonction exponentielle suivante lorsque x s’approche de plus l’infini :

$\displaystyle \lim_{x \to +\infty} 2^x$

Voir la solution

Bien qu’il s’agisse d’une fonction exponentielle, le processus pour résoudre la limite est le même : remplacer x par l’infini.

$\displaystyle \lim_{x \to +\infty} 2^x = 2^{+\infty}=\bm{+\infty}$

Exercice 16

Résolvez la limite infinie de la fonction exponentielle suivante :

$\displaystyle \lim_{x \to +\infty} 5^{-x}$

Voir la solution

Pour résoudre cette limite il faut utiliser les propriétés des fractions :

$\displaystyle \lim_{x \to +\infty} 5^{-x} = 5^{-(+\infty)}=5^{-\infty}= \cfrac{1}{5^{+\infty}}= \cfrac{1}{\infty} =\bm{0}$

Exercices d’indétermination

Exercice 17

Résolvez la limite suivante à l’infini :

$\displaystyle \lim_{x \to +\infty} \cfrac{-4x^2+3}{3x+1}$

Voir la solution

La limite donne l’indétermination moins l’infini entre plus l’infini. Le degré du numérateur est supérieur au degré du dénominateur, donc la limite indéterminée est égale à plus l’infini. Cependant, puisque la division est moins l’infini par l’infini positif, le résultat est moins l’infini.

$\displaystyle \lim_{x \to +\infty} \cfrac{-4x^2+3}{3x+1} = \cfrac{-4(+\infty)^2}{3(+\infty)} =\cfrac{-4(+\infty)}{+\infty}= \cfrac{-\infty}{+\infty}= \bm{-\infty}$

Exercice 18

Corrige la limite indéterminée suivante :

$\displaystyle \lim_{x \to +\infty} \cfrac{5x+8}{-5x+2}$

Voir la solution

Dans ce problème, la forme indéterminée infini sur l’infini est obtenue à partir du quotient de deux polynômes de même degré, donc le résultat de la limite indéterminée est la division de leurs coefficients principaux :

$\displaystyle \lim_{x \to +\infty} \cfrac{5x+8}{-5x+2} = \cfrac{5(+\infty)}{-5(+\infty)} = \cfrac{+\infty}{-\infty}=\cfrac{5}{-5}= \bm{-1}$

Exercice 19

Calculez la limite suivante au moins à l’infini :

$\displaystyle \lim_{x \to -\infty} \cfrac{x^2+3x+5}{x^4-x-6}$

Voir la solution

Le degré d’expression algébrique du numérateur est inférieur au degré d’expression du dénominateur, donc l’indétermination +∞/+∞ donne 0 :

$\displaystyle \lim_{x \to -\infty} \cfrac{x^2+3x+5}{x^4-x-6} = \cfrac{(-\infty)^2}{(-\infty)^4} = \cfrac{+\infty}{+\infty}= \bm{0}$

Exercice 20

Résolvez la limite indéterminée suivante d’une fonction avec racines :

$\displaystyle\lim_{x\to +\infty}\frac{\sqrt[3]{x^7-4x^3}}{x^2+5x}$

Voir la solution

L’expression du numérateur est sous un radical, son degré est donc 7/3. En revanche, le polynôme dénominateur est quadratique. Et puisque 7/3>2, la limite donne plus d’infini :

$\displaystyle \lim_{x \to +\infty}\frac{\sqrt[3]{x^7-4x^3}}{x^2+5x}=\frac{\sqrt[3]{(+\infty)^7}}{(+\infty)^2}=\frac{+\infty}{+\infty}=\bm{+\infty}$

Exercice 21

Déterminez la limite infinie de la fonction suivante avec des fractions :

$\displaystyle\lim_{x \to +\infty} \cfrac{-2x^2}{5-4x}$

Voir la solution

Dans cet exercice on obtient l’indétermination moins l’infini divisé par moins l’infini avec le degré du numérateur supérieur au degré du dénominateur, donc :

$\displaystyle \lim_{x \to +\infty} \cfrac{-2x^2}{5-4x} = \cfrac{-2(+\infty)^2}{-4(+\infty)} = \cfrac{-2(+\infty)}{-\infty}= \cfrac{-\infty}{-\infty} =\bm{+\infty}$

Exercice 22

Trouver la limite au moins infinie de la fonction suivante :

$\displaystyle \lim_{x \to -\infty} \cfrac{9x}{4-x^2}$

Voir la solution

Le polynôme dénominateur est quadratique, tandis que le polynôme numérateur est linéaire. Par conséquent, l’indétermination infini divisée par l’infini donne 0.

$\displaystyle \lim_{x \to -\infty} \cfrac{9x}{4-x^2} = \cfrac{9(-\infty)}{-(-\infty)^2} = \cfrac{-\infty}{-(+\infty)}=\cfrac{-\infty}{-\infty}= \bm{0}$

Exercice 23

Résolvez la limite au moins infinie de la fonction suivante :

$\displaystyle \lim_{x \to -\infty} \cfrac{-2x^3-3x}{-3x^2+4x-1}$

Voir la solution

Le numérateur est d’un degré supérieur au dénominateur, donc le résultat de la forme indéterminée ∞/∞ sera infini. De plus, le signe de l’infini sera négatif car positif entre négatif se traduit par négatif :

$\displaystyle \lim_{x \to -\infty} \cfrac{-2x^3-3x}{-3x^2+4x-1} = \cfrac{-2(-\infty)^3}{-3(-\infty)^2} =\cfrac{-2(-\infty)}{-3(+\infty)}= \cfrac{+\infty}{-\infty}= \bm{-\infty}$

Exercice 24

Résolvez la limite suivante à l’infini :

$\displaystyle\lim_{x \to +\infty}\cfrac{2^x-4}{-2x^6+x^4}$

Voir la solution

La fonction exponentielle est d’ordre supérieur à la fonction polynomiale, donc la limite donnera l’infini. Cependant, en divisant le positif par le négatif, le signe infini sera négatif :

$\displaystyle\lim_{x \to +\infty}\frac{2^x-4}{-2x^6+x^4}=\frac{2^{+\infty}}{-2(+\infty)^6}=\frac{+\infty}{-\infty}=\bm{-\infty}$

Exercice 25

Calculez la limite infinie de la fonction suivante avec une racine carrée :

$\displaystyle \lim_{x \to +\infty} \cfrac{\sqrt{4x^2+1}}{-2x}$

Voir la solution

Le numérateur est constitué d’une racine carrée, son degré est donc 2/2=1. Alors, le degré du numérateur est égal à celui du dénominateur, donc l’indétermination infinie entre l’infini se résout comme suit :

$\displaystyle \lim_{x \to +\infty} \cfrac{\sqrt{4x^2+1}}{-2x}= \cfrac{\sqrt{4(+\infty)^2}}{-2(\infty)}= \cfrac{+\infty}{-\infty} = \cfrac{\sqrt{4}}{-2}=\cfrac{2}{-2}=\bm{-1}$

Exercice 26

Résolvez la limite infinie de la fonction suivante avec deux radicaux :

$\displaystyle \lim_{x \to +\infty} \cfrac{\sqrt[3]{6x^7+2x^3}}{\sqrt{x^5-3x^4+2x}}$

Voir la solution

Le degré du numérateur est 7/3=2,33 et le degré du dénominateur est 5/2=2,5. Par conséquent, puisque le degré du numérateur est inférieur au degré du dénominateur, la limite infinie indéterminée entre l’infini est 0 :

$\displaystyle \lim_{x \to +\infty} \cfrac{\sqrt[3]{6x^7+2x^3}}{\sqrt{x^5-3x^4+2x}}=\cfrac{\sqrt[3]{6(+\infty)^7}}{\sqrt{(+\infty)^5}}=\cfrac{+\infty}{+\infty}=\bm{0}$

Exercice 27

Calculez la limite suivante :

$\displaystyle \lim_{x \to +\infty} \cfrac{\sqrt[5]{x^7-2x^5-1}}{4^{x-2}+3x}$

Voir la solution

Quel que soit le degré du numérateur, puisque nous avons une fonction exponentielle au dénominateur, le résultat de la forme indéterminée infinie sur l’infini est 0 :

$\displaystyle \lim_{x \to +\infty} \cfrac{\sqrt[5]{x^7-2x^5-1}}{4^{x-2}+3x}=\cfrac{\sqrt[5]{(+\infty)^7}}{4^{+\infty-2}}=\cfrac{+\infty}{+\infty}=\bm{0}$

Exercice 28

Déterminer la limite infinie de la fonction rationnelle suivante :

$\displaystyle\lim_{x\to +\infty}\left(\frac{x^3+1}{x-1}-\frac{x}{4} \right)$

Voir la solution

Tout d’abord, nous essayons de calculer la limite en substituant l’infini dans la fonction :

$\displaystyle\lim_{x\to +\infty}\left(\frac{x^3+1}{x-1}-\frac{x}{4}\right)=\frac{(+\infty)^3+1}{+\infty-1}-\frac{+\infty}{4} = \bm{+\infty -\infty}$

Mais on retrouve l’indétermination ∞ – ∞. Par conséquent, nous réduisons les fractions à un dénominateur commun :

$\begin{array}{l}\displaystyle\lim\limits_{x \to +\infty} \left(\frac{x^3+1}{x-1}-\frac{x}{4} \right)=\\[5ex]\displaystyle = \lim_{x\to +\infty}\left(\frac{(x^3+1)\cdot4}{(x-1)\cdot4}-\frac{x\cdot(x-1)}{4\cdot (x-1)}\right)=\\[5ex]\displaystyle =\lim_{x\to +\infty}\left(\frac{4x^3+4}{4x-4}-\frac{x^2-x}{4x-4}\right)\end{array}$

Et comme les deux fractions ont désormais le même dénominateur, on peut les réunir en une seule fraction :

$\displaystyle\lim_{x \to +\infty}\left(\frac{4x^3+4}{4x-4}-\frac{x^2-x}{4x-4}\right)=\lim_{x\to +\infty}\frac{4x^3+4-(x^2-x)}{4x-4}$

On fait la parenthèse du numérateur :

$\displaystyle\lim_{x \to +\infty} \frac{4x^3+4-x^2+x}{4x-4}$

Et enfin, on détermine la limite :

$\displaystyle\lim_{x \to +\infty}\frac{4x^3+4-x^2+x}{4x-4}=\frac{4(+\infty)^3}{4(+\infty)}=\frac{+\infty}{+\infty} = \bm{+\infty}$

Dans ce cas l’indétermination ∞/∞ donne +∞ car le degré du numérateur est supérieur au degré du dénominateur.

Exercice 29

Résolvez la limite de la fonction fractionnaire suivante lorsque x tend vers 0 :

$\displaystyle\lim_{x\to 0}\left(\frac{-3x-2}{x^4}-\frac{5}{x^2}\right)$

Voir la solution

Nous essayons d’abord de calculer la limite comme d’habitude :

$\displaystyle\lim_{x \to 0}\left(\frac{-3x-2}{x^4}-\frac{5}{x^2}\right)=\frac{-3\cdot0-2}{0^4}-\frac{5}{0^2}=\frac{-2}{0}-\frac{5}{0}=\bm{\infty-\infty}$

Mais on obtient la forme indéterminée ∞-∞. Il faut donc réduire les fractions de la fonction à un dénominateur commun.

Dans ce cas, x ⁴ est un multiple de x ² , donc simplement en multipliant le numérateur et le dénominateur de la deuxième fraction par x ² nous nous assurerons que les deux fractions ont le même dénominateur :

$\begin{array}{l}\displaystyle\lim_{x \to 0}\left(\frac{-3x-2}{x^4}-\frac{5}{x^2}\right)=\\[5ex]\displaystyle =\lim_{x \to 0}\left(\frac{-3x-2}{x^4}-\frac{5\cdot x^2}{x^2\cdot x^2} \right)=\\[5ex]\displaystyle =\lim_{x\to 0}\left(\frac{-3x-2}{x^4}-\frac{5x^2}{x^4}\right)\end{array}$

Nous pouvons maintenant soustraire les deux fractions :

$\displaystyle\lim_{x \to 0}\left(\frac{-3x-2}{x^4}-\frac{5x^2}{x^4}\right)=\lim_{x\to 0}\frac{-3x-2-5x^2 }{x^4}$

Nous essayons à nouveau de résoudre la limite :

$\displaystyle \lim_{x \to 0} \cfrac{-3x-2-5x^2 }{x^4} =\cfrac{-3\cdot 0-2-5\cdot 0^2}{0^4}=\frac{-2}{0}$

Mais on se retrouve avec l’indétermination d’une constante partant de zéro. Il faut donc calculer les limites latérales de la fonction.

$\displaystyle\lim_{x \to 0^{-}} \frac{-3x-2-5x^2}{x^4}=\frac{-2}{+0}=-\infty$

$\displaystyle\lim_{x \to 0^{+}}\frac{-3x-2-5x^2}{x^4}=\frac{-2}{+0}=-\infty$

En conclusion, puisque les deux limites latérales de la fonction au point x=0 donnent -∞, la solution de la limite est -∞ :

$\displaystyle \lim_{x \to 0^-}f(x)=\lim_{x \to 0^+}f(x)=-\infty\ \longrightarrow \ \lim_{x \to 0}f(x)= \bm{-\infty}$

Exercice 30

Résolvez la limite infinie de la fonction suivante avec des racines :

$\displaystyle\lim_{x\to +\infty}\left(4x^2-\sqrt{x^4+1}\right)$

Voir la solution

En essayant de résoudre la limite, nous obtenons l’indétermination infini moins l’infini :

$\displaystyle\lim_{x\to +\infty}\left(4x^2-\sqrt{x^4+1}\right)=4(+\infty)^2-\sqrt{(+\infty)^4}=\bm{+\infty -\infty}$

Par conséquent, puisqu’il y a des radicaux dans la fonction, il faut la multiplier et la diviser par l’expression radicale conjuguée :

$\displaystyle\lim_{x \to +\infty}\left(4x^2-\sqrt{x^4+1} \right)=\lim_{x \to +\infty}\frac{\left(4x^2-\sqrt{x^4+1}\right)\cdot\left(4x^2+\sqrt{x^4+1}\right)}{4x^2+\sqrt{x^4+1}}$

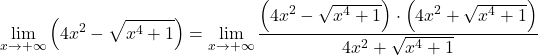
Au numérateur nous avons le produit notable d’une somme et d’une différence, qui est égal à la différence des carrés. Pourtant:

$\displaystyle\lim_{x\to +\infty}\frac{\left(4x^2\right)^2-\left(\sqrt{x^4+1}\right)^2}{4x^2+\sqrt{x^4+1}}$

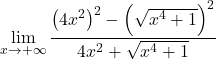
On simplifie le radical au carré :

$\displaystyle\lim_{x\to +\infty}\frac{\bigl(4x^2\bigr)^2-(x^4+1)}{4x^2+\sqrt{x^4+1}}$

On opère sur le numérateur :

$\displaystyle\lim_{x\to +\infty}\frac{16x^4-x^4-1}{4x^2+\sqrt{x^4+1}}$

$\displaystyle\lim_{x\to +\infty}\frac{15x^4-1}{4x^2+\sqrt{x^4+1}}$

Et finalement on trouve la limite :

$\displaystyle\lim_{x\to +\infty}\frac{15x^4-1}{4x^2+\sqrt{x^4+1}}=\frac{15(+\infty)^4}{4(+\infty)^2+\sqrt{(+\infty)^4}}=\frac{+\infty}{+\infty}= \bm{+\infty}$

Dans ce cas l’indétermination infini divisé par l’infini est plus infinie car le degré du numérateur est supérieur au degré du dénominateur (rappelons que la racine carrée réduit le degré de deux :

$\sqrt{x^4} = x^{4/2} = x^2$ ).

Exercice 31

Résolvez la limite lorsque x tend vers l’infini de la fonction irrationnelle suivante :

$\displaystyle\lim_{x\to +\infty}\left(2x-1-\sqrt{4x^2+1}\right)$

Voir la solution

Tout d’abord, nous essayons de calculer la limite comme d’habitude :

$\displaystyle\lim_{x\to +\infty}\left(2x-1-\sqrt{4x^2+1}\right)=2(+\infty)-\sqrt{4(+\infty)^2}=\bm{+\infty -\infty}$

Mais il en résulte l’indétermination de la différence des infinis. Par conséquent, puisque la fonction a des racines, il faut multiplier et diviser l’expression par le radical conjugué :

$\displaystyle\lim_{x\to +\infty}\frac{\left(2x-1-\sqrt{4x^2+1}\right)\cdot\left(2x-1+\sqrt{4x^2+1}\right)}{2x-1 +\sqrt{4x^2+1}}$

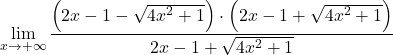
On regroupe l’égalité notable du numérateur de la fraction :

$\displaystyle\lim_{x\to +\infty}\frac{\left(2x-1\right)^2-\left(\sqrt{4x^2+1}\right)^2}{2x-1+\sqrt{4x^2+1}}$

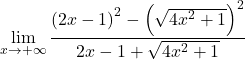
On résout la racine carrée :

$\displaystyle\lim_{x\to +\infty}\frac{\left(2x-1\right)^2-\left(4x^2+1\right)}{2x-1+\sqrt{4x^2+1}}$

On résout l’identité notable du carré d’une différence :

$\displaystyle\lim_{x\to +\infty}\frac{4x^2+1-4x-\left(4x^2+1\right)}{2x-1+\sqrt{4x^2+1}}$

On opère sur le numérateur :

$\displaystyle\lim_{x\to +\infty}\frac{4x^2+1-4x-4x^2-1}{2x-1+\sqrt{4x^2+1}}$

$\displaystyle\lim_{x \to +\infty}\frac{-4x}{2x-1+\sqrt{4x^2+1}}$

Et enfin, on calcule la valeur de la limite à l’infini :

$\displaystyle\lim_{x \to +\infty} \cfrac{-4x }{2x-1 +\sqrt{4x^2+1} } = \cfrac{-4(+\infty) }{2(+\infty)+\sqrt{4(+\infty)^2} } = \cfrac{-\infty}{+\infty} =$

Même s’il y a un x au carré au dénominateur, son degré est en réalité 1 car il est à l’intérieur d’une racine :

$\sqrt{4x^2} =\sqrt{4}\cdot \sqrt{x^2} = \sqrt{4}\cdot x^{2/2} =\sqrt{4} x^1=\sqrt{4}x .$

Par conséquent, le résultat de l’indétermination -∞/+∞ est la division des coefficients des x du plus haut degré, puisque le degré du numérateur est le même que le degré du dénominateur.

$\displaystyle\lim_{x\to +\infty}\frac{-4x}{2x-1+\sqrt{4x^2+1} }=\frac{-\infty}{+\infty}=\frac{-4}{2+\sqrt{4}}=\frac{-4}{2+2}=\frac{-4}{4}=\bm{-1}$

Notez que puisqu’il y a deux termes du premier degré au dénominateur

$\bigl(2x$ et $\sqrt{4x^2}\bigr)$ , pour résoudre l’indétermination -∞/+∞ il faut prendre tous les coefficients des termes du premier degré, c’est-à-dire les $2$ de $2x$ et le $\sqrt{4}$ de $\sqrt{4x^2}.$

Exercice 32

Calculez la limite lorsque x s’approche de 1 de la fonction suivante avec des fractions :

$\displaystyle\lim_{x\to 1}\left(\frac{1}{1-x}-\frac{3}{1-x^3}\right)$

Voir la solution

En essayant de faire la limite on obtient la limite indéterminée de l’infini moins l’infini :

$\displaystyle\lim_{x\to 1}\left(\frac{1}{1-x}-\frac{3}{1-x^3}\right)=\frac{1}{1-1}--\frac{3}{1-1^3}=\frac{1}{0}-\frac{3}{0}=\bm{\infty-\infty}$

Il faut donc réduire les fractions à un dénominateur commun, ou en d’autres termes, il faut multiplier le numérateur et le dénominateur d’une fraction par le dénominateur de l’autre :

$\begin{array}{l}\displaystyle\lim_{x \to 1}\left(\frac{1}{1-x}-\frac{3}{1-x^3} \right)=\\[5ex]\displaystyle =\lim_{x\to 1}\left( \frac{1\cdot(1-x^3)}{(1-x)\cdot(1-x^3)}-\frac{3\cdot(1-x)}{(1-x^3)\cdot(1-x)}\right)=\\[5ex]\displaystyle =\lim_{x \to 1}\left(\frac{1-x^3}{1-x-x^3+x^4}-\frac{3-3x}{1-x-x^3+x^4}\right)\end{array}$

Et comme maintenant les deux fractions ont le même dénominateur, on peut les mettre ensemble :

$\displaystyle\lim_{x \to 1}\left(\frac{1-x^3}{1-x-x^3+x^4}-\frac{3-3x}{1-x-x^3+x^4}\right)=\lim_{x\to 1}\frac{1-x^3-(3-3x)}{1-x-x^3+x^4}$

Nous opérons :

$\displaystyle\lim_{x \to 1} \cfrac{1-x^3-3+3x}{1-x-x^3+x^4}$

$\displaystyle\lim_{x \to 1} \cfrac{-x^3+3x-2}{x^4-x^3-x+1}$

Et nous essayons à nouveau de résoudre la limite :

$\displaystyle\lim_{x \to 1}\frac{-x^3+3x-2}{x^4-x^3-x+1}=\frac{-1^3+3\cdot1-2}{1^4-1^3-1+1}=\mathbf{\frac{0}{0}}$

Mais on retrouve l’indétermination zéro divisé par zéro. Il faut donc factoriser les polynômes du numérateur et du dénominateur :

$\displaystyle\lim_{x \to 1}\frac{-x^3+3x-2}{x^4-x^3-x+1}=\lim_{x \to 1}\frac{-(x-1)^2(x+2)}{(x-1)^2(x^2+x+1)}$

Maintenant, nous simplifions la fraction en supprimant le facteur qui est répété au numérateur et au dénominateur :

$\displaystyle\lim_{x \to 1}\frac{-\cancel{(x-1)^2}(x+2)}{\cancel{(x-1)^2}(x^2+x+1)}=\lim_{x \to 1}\frac{-(x+2)}{x^2+x+1}$

Et enfin, nous résolvons la limite :

$\displaystyle\lim_{x \to 1}\frac{-(x+2)}{x^2+x+1}=\frac{-(1+2)}{1^2+1+1}=\frac{-3}{3}=\bm{-1}$

Exercice 33

Calculez la limite de la fonction rationnelle suivante au point x=-2.

$\displaystyle\lim_{x \to -2}\frac{x^2 +2x}{x^2-x-6}$

Voir la solution

Logiquement, nous essayons d’abord de résoudre la limite :

$\displaystyle\lim_{x \to -2} \frac{x^2 +2x}{x^2-x-6}=\frac{(-2)^2+2\cdot (-2)}{(-2)^2-(-2)-6}=\frac{4-4}{4+2-6}=\frac{0}{0}$

Mais on se retrouve avec l’indétermination 0/0. Il faut donc factoriser les polynômes du numérateur et du dénominateur :

$\displaystyle\lim_{x \to -2}\frac{x^2 +2x}{x^2-x-6}=\lim_{x \to -2}\frac{x(x+2)}{(x+2)(x-3)}$

Maintenant, nous simplifions la fraction en supprimant les parenthèses qui sont répétées au numérateur et au dénominateur :

$\displaystyle\lim_{x \to -2}\frac{x\cancel{(x+2)}}{\cancel{(x+2)}(x-3)}=\lim_{x \to -2}\frac{x}{x-3}$

Et enfin, on recalcule la limite avec la fraction simplifiée :

$\displaystyle\lim_{x \to -2}\frac{x}{x-3}=\cfrac{-2}{-2-3}=\cfrac{-2}{-5}=\mathbf{\cfrac{2}{5}}$

Exercice 34

Résolvez la limite de la fonction suivante lorsque x tend vers -1 :

$\displaystyle\lim_{x \to -1}\frac{x^3+2x^2-x-2}{x^3-5x^2+2x+8}$

Voir la solution

Nous essayons d’abord de résoudre la limite comme d’habitude :

$\displaystyle\lim_{x \to -1}\frac{x^3+2x^2-x-2}{x^3-5x^2+2x+8}=\frac{(-1)^3+2(-1)^2-(-1)-2}{(-1)^3-5(-1)^2+2(-1)+8} =\frac{0}{0}$

Mais on obtient l’indétermination 0 entre 0. Il faut donc factoriser les 2 polynômes de la fraction :

$\displaystyle\lim_{x \to -1}\frac{x^3+2x^2-x-2}{x^3-5x^2+2x+8}=\lim_{x \to -1}\frac{(x-1)(x+1)(x+2)}{(x+1)(x-2)(x-4)}$

Nous pouvons maintenant simplifier les polynômes :

$\displaystyle\lim_{x \to -1}\frac{(x-1)\cancel{(x+1)}(x+2)}{\cancel{(x+1)}(x-2)(x-4)}=\lim_{x \to -1}\frac{(x-1)(x+2)}{(x-2)(x-4)}$

Et on résout la limite :

$\displaystyle\lim_{x \to -1} \frac{(x-1)(x+2)}{(x-2)(x-4)}=\frac{ (-1-1)(-1+2)}{(-1-2)(-1-4)}=\frac{(-2)\cdot (1)}{(-3)\cdot (-5)}=\frac{\bm{-2}}{\bm{15}}$

Exercice 35

Déterminer la solution de la limite de la fonction radicale suivante :

$\displaystyle\lim_{x\to 2}\frac{x^2-3x+2}{2-\sqrt{2x}}$

Voir la solution

Tout d’abord, nous vérifions si la limite donne une sorte d’indétermination :

$\displaystyle\lim_{x\to 2}\frac{x^2-3x+2}{2-\sqrt{2x}}=\frac{2^2-3\cdot2+2}{2-\sqrt{2\cdot 2}}=\frac{4-6+2}{2-2}=\frac{0}{0}$

La limite donne l’indétermination zéro divisé par zéro et on a une racine dans la fonction. Il faut donc multiplier le numérateur et le dénominateur de la fraction par le conjugué de l’expression radicale :

$\displaystyle\lim_{x\to 2}\frac{\left(x^2-3x+2\right)\cdot \left(2+\sqrt{2x}\right)}{\left(2-\sqrt{2x}\right)\cdot \left(2+\sqrt{2x}\right)}$

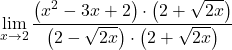
Le dénominateur correspond au développement de l’identité notable du produit d’une somme et d’une différence, on peut donc le simplifier :

$\displaystyle\lim_{x\to 2}\frac{\left(x^2-3x+2\right)\cdot \left(2+\sqrt{2x}\right)}{2^2-\left(\sqrt{2x}\right)^2}$

$\displaystyle\lim_{x\to 2}\frac{\left(x^2-3x+2\right)\cdot \left(2+\sqrt{2x}\right)}{4-2x}$

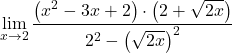
Cependant, nous ne pouvons pas encore simplifier les termes de la fraction. Il faut donc factoriser les polynômes :

$\displaystyle\lim_{x\to 2}\frac{\left(x^2-3x+2\right)\cdot \left(2+\sqrt{2x}\right)}{4-2x}=\lim_{x\to 2}\frac{(x-1)(x-2)\cdot\left(2+\sqrt{2x}\right)}{-2(x-2)}$

De cette façon, nous pouvons simplifier la fraction :

$\displaystyle\lim_{x\to 2}\frac{(x-1)\cancel{(x-2)}\left(2+\sqrt{2x}\right)}{-2\cancel{(x-2)}}=\lim_{x\to 2}\frac{(x-1)\left(2+\sqrt{2x}\right)}{-2}$

Et maintenant nous pouvons déterminer le résultat de la limite :

$\displaystyle\lim_{x\to 2}\frac{(x-1)\left(2+\sqrt{2x}\right)}{-2}=\frac{(2-1)\left(2+\sqrt{2\cdot 2}\right)}{-2}=\frac{1\cdot (2+2)}{-2}=\bm{-2}$

Exercice 36

Calculez la limite lorsque x tend vers 0 de la fonction radicale suivante :

$\displaystyle\lim_{x\to 0}\frac{x^2+6x}{3-\sqrt{4x+9}}$

Voir la solution

Tout d’abord, nous essayons de calculer la limite de la fonction comme nous le faisons toujours :

$\displaystyle\lim_{x\to 0}\frac{x^2+6x}{3-\sqrt{4x+9}}=\frac{0+0}{3-\sqrt{4\cdot 0+9}}=\frac{0}{3-3}=\frac{0}{0}$

Mais nous obtenons la forme indéterminée de 0/0. Par conséquent, on multiplie le numérateur et le dénominateur de la fonction par le conjugué de l’expression irrationnelle :

$\displaystyle\lim_{x\to 0}\frac{\left(x^2+6x\right)\cdot\left(3+\sqrt{4x+9}\right)}{\left(3-\sqrt{4x+9}\right)\cdot\left(3+\sqrt{4x+9}\right)}$

Nous appliquons la formule d’identité notable correspondante pour simplifier le dénominateur :

$\displaystyle\lim_{x\to 0}\frac{\left(x^2+6x\right)\cdot\left(3+\sqrt{4x+9}\right)}{3^2-\left(\sqrt{4x+9}\right)^2}$

$\displaystyle\lim_{x\to 0}\frac{\left(x^2+6x\right)\cdot\left(3+\sqrt{4x+9}\right)}{9-(4x+9)}$

$\displaystyle\lim_{x\to 0}\frac{\left(x^2+6x\right)\cdot\left(3+\sqrt{4x+9}\right)}{-4x}$

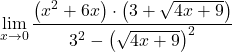
Maintenant, nous factorisons le binôme du numérateur en prenant le facteur commun :

$\displaystyle\lim_{x\to 0}\frac{\left(x^2+6x\right)\cdot\left(3+\sqrt{4x+9}\right)}{-4x}=\lim_{x\to 0}\frac{\bigl[x(x+6)\bigr]\cdot\left(3+\sqrt{4x+9}\right)}{-4x}$

Nous simplifions les facteurs qui sont répétés au numérateur et au dénominateur de la fonction :

$\displaystyle\lim_{x\to 0}\frac{\cancel{x}\left(x+6\right)\left(3+\sqrt{4x+9}\right)}{-4\cancel{x}}=\lim_{x\to 0}\frac{(x+6)\left(3+\sqrt{4x+9}\right)}{-4}$

Et, pour finir, on résout la limite de la fonction :

$\begin{array}{l}\displaystyle\lim_{x\to 0}\frac{(x+6)\left(3+\sqrt{4x+9}\right)}{-4}=\\[3ex]\displaystyle=\frac{(0+6)\left(3+\sqrt{4\cdot 0+9}\right)}{-4}=\\[3ex]\displaystyle=\frac{6\cdot (3+3)}{-4}=\frac{36}{-4}=\bm{-9}\end{array}$

Exercice 37

Résolvez la limite suivante en appliquant la méthode d’indétermination 0/0 :

$\displaystyle\lim_{x \to -1}\frac{x^3+2x^2-x-2}{x^3+5x^2+7x+3}$

Voir la solution

Nous essayons d’abord de résoudre la limite :

$\displaystyle\lim_{x \to -1}\frac{x^3+2x^2-x-2}{x^3+5x^2+7x+3}=\frac{(-1)^3+2(-1)^2-(-1)-2}{(-1)^3+5(-1)^2+7(-1)+3}=\frac{0}{0}$

Mais à la limite on obtient l’indétermination zéro sur zéro. Par conséquent, nous factorisons les polynômes du numérateur et du dénominateur :

$\displaystyle\lim_{x \to -1}\frac{x^3+2x^2-x-2}{x^3+5x^2+7x+3}=\lim_{x \to -1}\frac{(x-1)(x+1)(x+2)}{(x+1)^2(x+3)}$

Maintenant, nous simplifions la fraction en éliminant les facteurs qui se répètent au numérateur et au dénominateur :

$\displaystyle\lim_{x \to -1} \cfrac{(x-1)\cancel{(x+1)}(x+2)}{(x+1)^{\cancel{2}}(x+3)}=\lim_{x \to -1}\cfrac{(x-1)(x+2)}{(x+1)(x+3)}$

Et on calcule à nouveau la limite :

$\displaystyle\lim_{x \to -1}\frac{(x-1)(x+2)}{(x+1)(x+3)}=\frac{(-1-1)(-1+2)}{(-1+1)(-1+3)}=\frac{-2\cdot 1}{0 \cdot 2}=\frac{-2}{0} =\infty$

Mais maintenant on se retrouve avec l’indétermination d’un nombre divisé par 0. Il faut donc calculer les limites latérales de la fonction lorsque x tend vers -1.

Nous résolvons d’abord la limite latérale de la fonction au point x=-1 à gauche :

$\displaystyle\lim_{x \to -1^{-}}\frac{(x-1)(x+2)}{(x+1)(x+3)}=\frac{(-1-1)\cdot (-1+2)}{(-1+1)\cdot (-1+3)}=\frac{-2}{-0}=+\infty$

Et puis on calcule la limite latérale de la fonction au point x=-1 à droite :

$\displaystyle\lim_{x \to -1^{+}}\frac{(x-1)(x+2)}{(x+1)(x+3)}=\frac{(-1-1)\cdot (-1+2)}{(-1+1)\cdot (-1+3)}=\frac{-2}{+0}=-\infty$

Donc, puisque les deux limites latérales ne coïncident pas, la limite de la fonction en x=-1 n’existe pas :

$\displaystyle\displaystyle \lim_{x \to -1^-}f(x)= +\infty\neq\lim_{x \to -1^+}f(x)=-\infty\ \bm{\longrightarrow} \ \cancel{\exists} \lim_{x \to -1} f(x)$

Quelle est la limite d’une fonction ?

Comment calculer la limite d’une fonction

Limites latérales d’une fonction

Limites latérales égales

Limite d’une fonction par morceaux

Limite d’une fonction à l’infini

Limites indéterminées

A quoi servent les limites de fonction ?

Exercices résolus sur les limites des fonctions

Exercices de limites simples

Exercice 1

Exercice 2

Exercices de limites latérales des fonctions

Exercice 3

Exercice 4

Exercice 5

Exercice 6

Exercice 7

Exercices sur les limites des fonctions à l’infini

Exercice 8

Exercice 9

Exercice 10

Exercice 11

Exercice 12

Exercice 13

Exercice 14

Exercice 15

Exercice 16

Exercices d’indétermination

Exercice 17

Exercice 18

Exercice 19

Exercice 20

Exercice 21

Exercice 22

Exercice 23

Exercice 24

Exercice 25

Exercice 26

Exercice 27

Exercice 28

Exercice 29

Exercice 30

Exercice 31

Exercice 32

Exercice 33

Exercice 34

Exercice 35

Exercice 36

Exercice 37

Leave a Comment Cancel Reply