Dans cet article, nous expliquons ce que sont les fonctions bornées (supérieures et inférieures). De plus, nous vous montrons ce que signifie pour une fonction d’être bornée en un point et, enfin, vous trouverez les propriétés de ce type de fonction.
Qu’est-ce qu’une fonction bornée ?
Une fonction bornée est une fonction dont le graphe est dans des bornes. Autrement dit, une fonction est bornée au-dessus s’il existe un nombre K tel qu’il n’y a pas de valeur de la fonction supérieure à K (f(x)≤K), et une fonction est bornée en dessous s’il existe un nombre K tel qu’il est inférieur à toutes les valeurs de la fonction (f(x)≥K). Par conséquent, une fonction bornée est une fonction qui est bornée au-dessus et au-dessous.
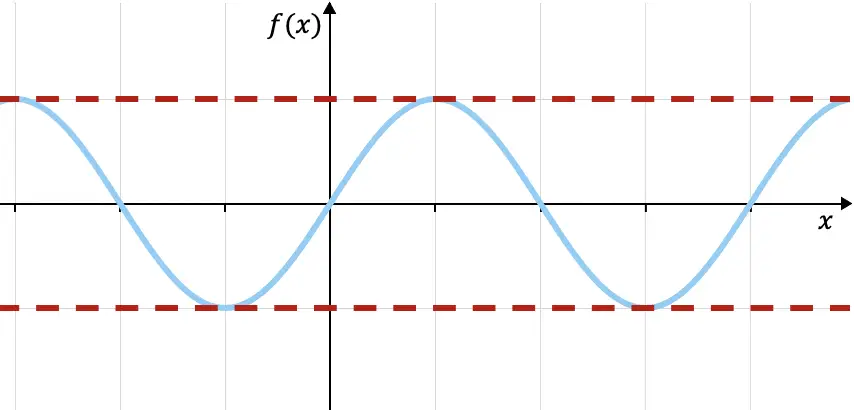
Par exemple, la fonction trigonométrique de sinus, représentée graphiquement ci-dessus, est bornée en haut par f(x)=1 et est bornée en bas par f(x)=-1 (lignes pointillées rouges), puisque toutes les valeurs de la fonction sont dans ces deux limites. Vous pouvez voir plus de propriétés de cette fonction dans le lien suivant :
➤ Voir : Caractéristiques de la fonction sinus
fonction bornée au-dessus
Cependant, toutes les fonctions ne sont pas délimitées au-dessus et au-dessous, une fonction ne peut être délimitée qu’au-dessus ou au-dessous.
Les fonctions bornées ci-dessus sont celles qui ne dépassent pas une certaine valeur, c’est-à-dire que la condition suivante est remplie :
où la valeur K est la borne supérieure de la fonction.
Par exemple, la parabole suivante est bornée en haut par K=7, mais la fonction n’est pas bornée en bas puisque ses branches s’allongent à l’infini.
Logiquement, si la fonction est bornée par K=7, elle est aussi bornée par K=8 et par des valeurs supérieures.
La plus petite borne supérieure est appelée borne supérieure et est représentée par sup(f) . De plus, si la fonction atteint ladite limite supérieure dans son domaine, on dira que ce point est le maximum absolu de la fonction.
➤ Voir : quels sont les maxima et les minima d’une fonction ?
Dans notre cas, la fonction est géométriquement bornée par K=7, il s’agit donc de l’extrême supérieur et du maximum absolu de la fonction.
fonction délimitée ci-dessous
Les fonctions délimitées ci-dessous sont celles qui n’ont pas de valeur inférieure à un certain nombre, c’est-à-dire qu’elles vérifient l’expression mathématique suivante :
Où la valeur K est la borne inférieure de la fonction.
Ci-dessous, vous avez la représentation graphique d’une fonction exponentielle qui est délimitée ci-dessous par K=3 :
Évidemment, la fonction est également bornée par des valeurs inférieures à K=3.
Comme précédemment, la borne inférieure la plus grande est appelée borne inférieure et est représentée par inf(f) . De plus, si la fonction atteint ledit extrême inférieur dans son domaine, nous dirons que ce point est le minimum absolu de la fonction.
Dans ce cas, K=3 n’est pas le minimum absolu de la fonction, car la fonction atteint cette valeur à l’infini et, donc, elle est hors de son domaine. Autrement dit, f(x)=3 est une asymptote horizontale de la fonction .
Il existe un théorème qui permet de savoir si une fonction est bornée en haut et en bas sans sa représentation graphique. Cliquez ici pour voir en quoi consiste le théorème de Weierstrass.
➤ Voir : Théorème de Weierstrass
Fonction bornée en un point
Nous venons d’étudier la notion de bornage d’une fonction en général, mais il est également possible d’analyser si une fonction est bornée ou non dans un voisinage plus petit, c’est-à-dire dans une partie de la fonction.
Ouais
est un point dans le domaine de la fonction et
n’importe quelle valeur, on dira que la fonction est bornée dessus/dessous au point s’il y a un environnement
où la fonction est bornée au-dessus/au-dessous.
Par conséquent, une fonction est bornée au point
s’il est délimité en haut et en bas dans un voisinage
Évidemment, si une fonction est bornée de façon générale, elle sera aussi bornée en chacun de ses points. Cependant, l’inverse est faux, c’est-à-dire qu’une fonction peut être bornée en chacun de ses points et ne pas être bornée sur tout son domaine.
Par exemple, la fonction affine suivante est partiellement bornée en chacun de ses points, mais ce n’est pas une fonction bornée.
Propriétés des fonctions bornées
Les fonctions bornées ont les propriétés suivantes :
- Ouais
et
sont deux fonctions bornées, l’addition (ou la soustraction) des deux fonctions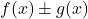
est aussi une fonction bornée. - Ouais et sont deux fonctions bornées, le produit des deux fonctions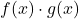
se trouve également être une fonction bornée. - Si une fonction a une asymptote verticale, elle ne peut pas être totalement bornée. D’autre part, la fonction peut être bornée au-dessus ou au-dessous.
- Toute fonction continue et bornée sur un intervalle est intégrable.