Sur cette page, vous verrez quelle est la dérivée de l’arc cosinus hyperbolique (formule). Vous trouverez également des exercices résolus pas à pas de dérivées de l’arc cosinus hyperbolique d’une fonction. Et, enfin, vous trouverez la démonstration de la formule de la dérivée de ce type de fonction trigonométrique.
Formule de la dérivée de l’arc cosinus hyperbolique
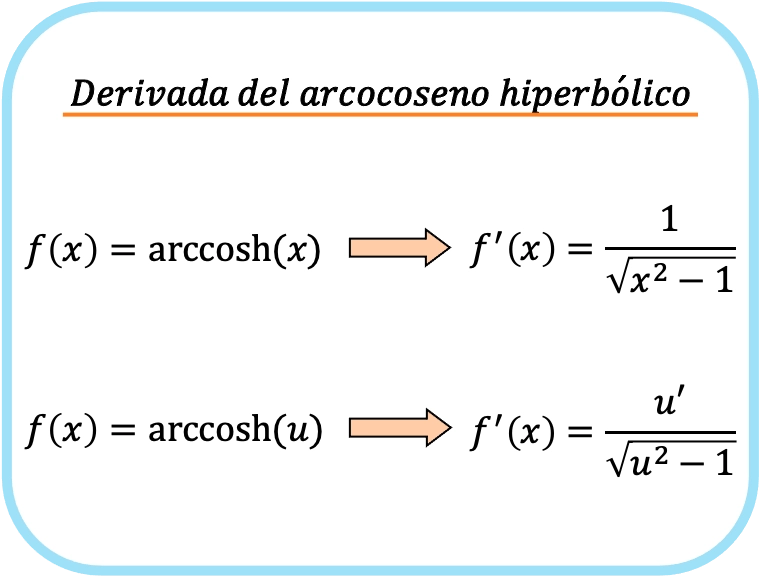
La dérivée de l’arccosinus hyperbolique de x est un sur la racine carrée de x au carré moins 1.
![]()
Par conséquent, la dérivée de l’arc cosinus hyperbolique d’une fonction est égale au quotient de la dérivée de cette fonction divisé par la racine carrée de cette fonction au carré moins un.
![]()
La deuxième formule inclut la règle de la chaîne et peut donc être utilisée pour dériver n’importe quel arccosinus hyperbolique. En fait, si nous substituons le u à x, nous obtiendrons la première formule. Au lieu de cela, la première formule ne fonctionne que pour la dérivée de l’arccosinus hyperbolique de x.
L’arccosinus hyperbolique est la fonction inverse du cosinus hyperbolique, et donc les deux fonctions sont liées. Vous pouvez voir la formule de la dérivée de cette fonction trigonométrique en cliquant ici :
➤ Voir : formule de la dérivée du cosinus hyperbolique
Exemples de la dérivée de l’arcsinus hyperbolique
Exemple 1
![]()
Pour trouver la dérivée de l’arccosinus hyperbolique, nous devons utiliser sa formule correspondante, qui est :
![]()
Par conséquent, au numérateur de la fraction, nous devons mettre la dérivée de 5x, qui est 5. Et au dénominateur, nous devons simplement mettre la racine carrée de la fonction de l’argument au carré moins 1 :
![]()
Exemple 2
![]()
La fonction à dériver de cet exercice est un arccosinus hyperbolique, nous utilisons donc la formule suivante pour la dériver :
![]()
Ainsi, au numérateur on écrit la dérivée de l’argument de la fonction et au dénominateur la racine carrée de la fonction de l’argument élevée à 2 moins 1 :
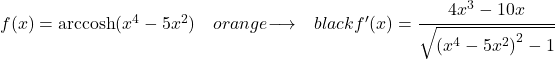
Preuve de la dérivée de l’arc cosinus hyperbolique
Enfin, nous démontrerons la formule de la dérivée de l’arc cosinus hyperbolique.
![]()
Tout d’abord, nous transformons l’arc cosinus hyperbolique en cosinus hyperbolique :
![]()
On déduit des deux côtés de l’égalité :
![]()
Nous vous dédouanons :
![]()
Nous utilisons maintenant l’identité trigonométrique qui relie le sinus hyperbolique et le cosinus hyperbolique pour modifier le dénominateur :
![]()
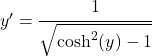
Cependant, dans un premier temps, nous avons déduit que x est équivalent au cosinus hyperbolique de y, donc l’équation reste :
![]()