Vous trouverez ici comment calculer la dérivée de l’arcsecante hyperbolique d’une fonction. De plus, vous pourrez voir des exemples résolus de la dérivée de l’arcsecante hyperbolique.
Formule dérivée arcsecante hyperbolique
La dérivée de l’arcsecante hyperbolique de x est égale à moins 1 divisé par le produit de x fois la racine de un moins x au carré.
![]()
Par conséquent, la dérivée de l’arcsecante hyperbolique d’une fonction est moins la dérivée de cette fonction divisée par le produit de la fonction fois la racine de un moins la fonction au carré.
![]()
En bref, la formule de la dérivée de la fonction arcsecante hyperbolique est la suivante :
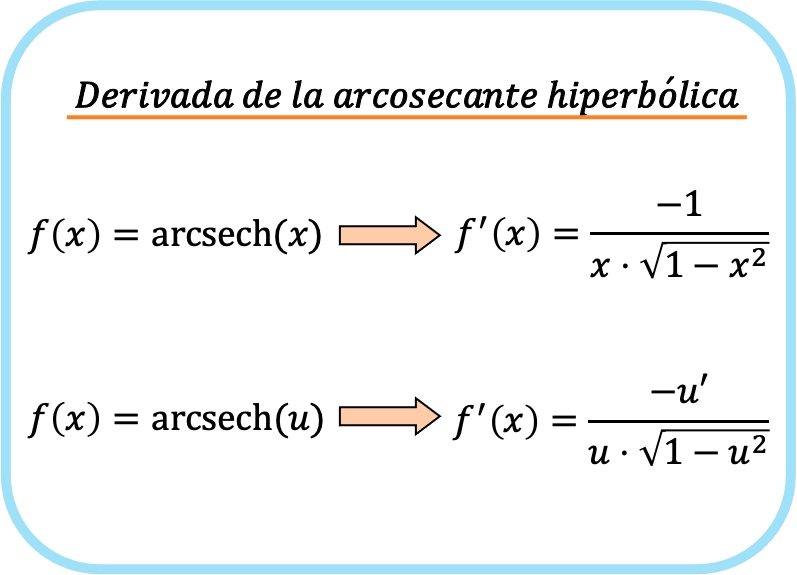
Les deux expressions correspondent en fait à la même formule, mais la règle de la chaîne est appliquée à la deuxième formule. En fait, si vous substituez la fonction identité x à u, vous obtiendrez la première formule puisque la dérivée de x est 1.
Exemples de dérivée de l’arcsecante hyperbolique
Après avoir vu quelle est la formule de la dérivée de l’arcsecante hyperbolique, nous allons résoudre deux exercices pas à pas de ce type de dérivées trigonométriques inverses. Ainsi, vous pouvez voir exactement comment dériver l’arcsecante hyperbolique d’une fonction.
Exemple 1
Dans cet exemple, nous déterminerons quelle est la dérivée de l’arcsecante hyperbolique 2x.
![]()
Dans l’argument arcsecant hyperbolique, nous avons une fonction autre que x, nous devons donc utiliser la formule de règle de chaîne pour la dériver :
![]()
La fonction 2x est linéaire, donc sa dérivée est 2. Par conséquent, pour trouver la dérivée, nous devons simplement substituer 2x à u et 2 à u’ dans la formule :
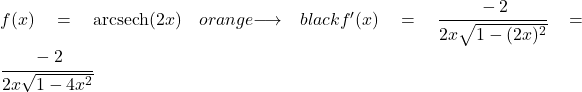
Exemple 2
Dans ce deuxième exercice, nous dériverons l’arcsecante hyperbolique d’une fonction polynomiale :
![]()
La fonction de cet exercice est composée, car l’arcsecante hyperbolique a une autre fonction dans son argument. Nous devons donc utiliser la formule dérivée arcsecante hyperbolique avec la règle de la chaîne pour faire sa dérivation :
![]()
Par conséquent, au numérateur de la fraction, nous mettons la dérivée de la fonction polynomiale de l’argument, et au dénominateur, nous changeons le u par la fonction polynomiale :
![Rendered by QuickLaTeX.com \begin{aligned}f(x)=\text{arcsech}(x^3-4x) \quad\color{orange}\bm{\longrightarrow}\quad\color{black}f'(x)&=\cfrac{-(3x^2-4)}{(x^3-4x)\sqrt{1-(x^3-4x)^2}}\\[1.5ex] &=\cfrac{-3x^2+4}{(x^3-4x)\sqrt{1-(x^3-4x)^2}}\end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-1f6389de5c7761fb5d35a9861156eec1_l3.png)