Dans cet article, nous expliquons comment dériver la sécante hyperbolique d’une fonction. Vous trouverez la formule de la dérivée de la sécante hyperbolique et plusieurs exemples travaillés de ce type de dérivée.
Formule de la dérivée de la sécante hyperbolique
La dérivée de la sécante hyperbolique de x est égale à moins le produit de la sécante hyperbolique de x fois la tangente hyperbolique de x.
![]()
Par conséquent, la dérivée de la sécante hyperbolique d’une fonction est moins le produit de la sécante hyperbolique de la fonction par la tangente hyperbolique de la fonction par la dérivée de ladite fonction.
![]()
En bref, la formule de la dérivée de la fonction sécante hyperbolique est la suivante :
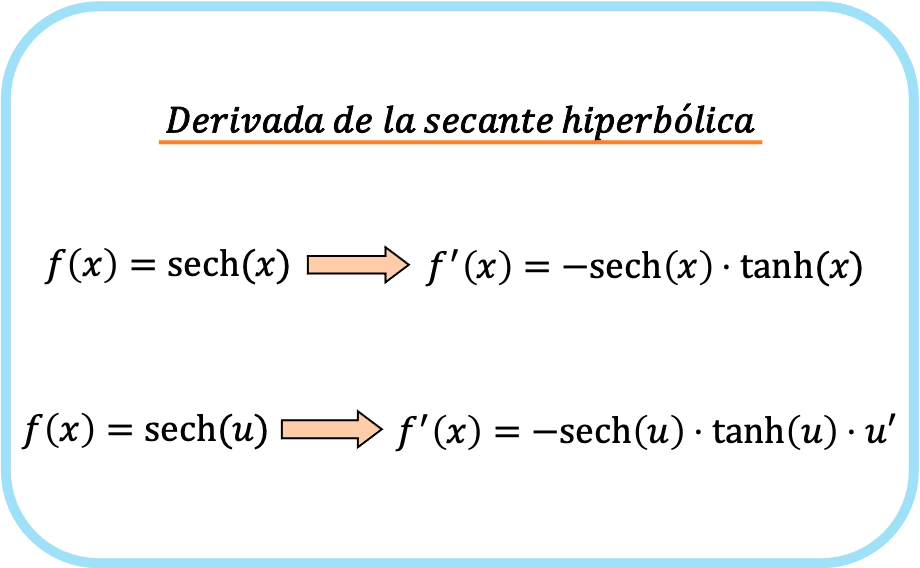
Notez que les deux expressions appartiennent en fait à une seule formule. La seule différence est que dans la deuxième formule, la règle de la chaîne est appliquée.
Exemples de dérivée de la sécante hyperbolique
Maintenant que nous connaissons la formule de la dérivée de la sécante hyperbolique, nous allons voir plusieurs exercices résolus de ce type de dérivée trigonométrique.
Exemple 1
![]()
Dans cet exemple, nous avons une fonction différente de x dans l’argument de la sécante hyperbolique, donc pour la dériver, nous devons utiliser la formule de la règle de la chaîne.
![]()
Puisque la fonction 2x est linéaire, sa dérivée est 2. Par conséquent, pour trouver la dérivée, nous devons simplement remplacer le u par 2x et le u’ par 2 dans la formule :
![]()
Exemple 2
![]()
La fonction de cet exercice est composée, puisque la sécante hyperbolique a une autre fonction dans son argument. Il faut donc utiliser la formule sécante hyperbolique avec la règle de la chaîne pour faire sa dérivation :
![]()
La dérivée de x élevée à 2 donne 2x, donc la dérivée de la sécante hyperbolique de x au carré est :
![]()