Nous expliquons ici comment dériver la cotangente hyperbolique d’une fonction. Vous trouverez également des exemples de la dérivée de la cotangente hyperbolique.
Formule de la dérivée de la cotangente hyperbolique
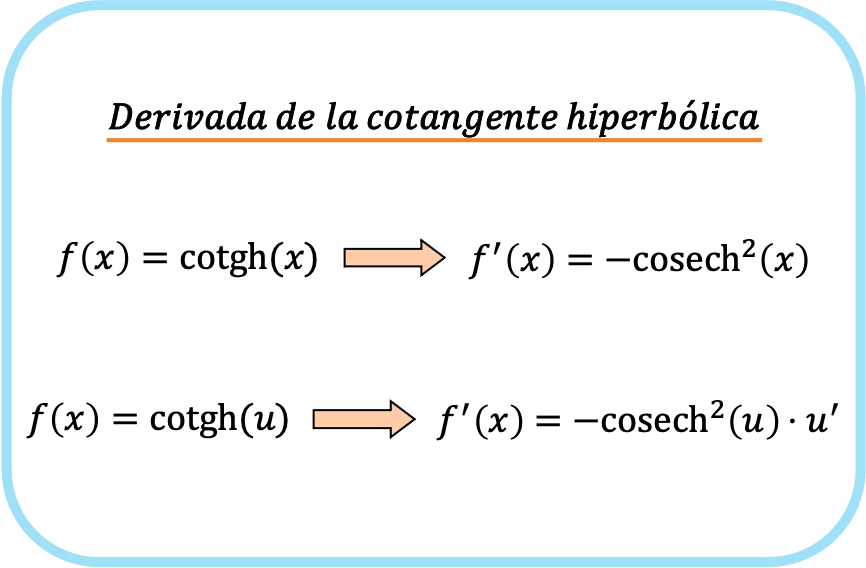
La dérivée de la cotangente hyperbolique de x est égale à moins la cosécante hyperbolique de x au carré.
![]()
Par conséquent, la dérivée de la cotangente hyperbolique d’une fonction est moins la cosécante hyperbolique de la fonction multipliée par la dérivée de cette fonction.
![]()
Gardez à l’esprit que dans la deuxième formule, la règle de la chaîne a été appliquée et que cette formule est utilisée lorsqu’il existe une fonction différente de x dans l’argument cotangente hyperbolique.
Il se peut que dans certains livres de mathématiques vous trouviez que la dérivée de la cotangente en soit une autre, puisque les trois expressions suivantes sont équivalentes :
![]()
Évidemment, vous pouvez utiliser l’expression que vous préférez parmi les trois pour dériver la cotangente hyperbolique, mais la plus utilisée est la cosécante hyperbolique au carré.
Exemples de dérivée de la cotangente hyperbolique
Une fois que nous savons quelle est la formule de la dérivée de la cotangente hyperbolique d’une fonction, nous allons résoudre plusieurs exemples de ce type de dérivées trigonométriques.
Exemple 1
Dans cet exemple nous verrons quelle est la dérivée de la cotangente hyperbolique de la fonction 2x.
![]()
Dans l’argument de la cotangente hyperbolique, nous avons une fonction autre que x, nous devons donc utiliser la formule avec la règle de la chaîne pour faire la dérivation :
![]()
Puisque 2x est un terme du premier degré, sa dérivée est 2. Donc, pour trouver la dérivée de la cotangente hyperbolique de 2x, nous mettons simplement 2x dans l’argument au carré de la cosécante hyperbolique et multiplions par 2.
![]()
Exemple 2
Dans le deuxième exemple, nous déterminerons la valeur de la dérivée de la cotangente hyperbolique d’une fonction polynomiale.
![]()
Comme nous l’avons vu plus haut, la règle pour dériver la cotangente hyperbolique d’une fonction est la suivante :
![]()
Par conséquent, la dérivée de la cotangente hyperbolique de cet exercice sera la suivante :
![]()