Sur cette page nous expliquons quelles sont les parties d’un monôme (coefficient, partie littérale, degré,…) et comment les identifier facilement. De plus, vous pourrez voir des exemples et même vous entraîner avec des exercices résolus étape par étape sur les parties d’un monôme.
Quelles sont les parties d’un monôme ?
Les parties d’un monôme sont :
- Coefficient : est le nombre qui multiplie les variables (ou lettres) du monôme.
- Variable : sont chacune des lettres qui apparaissent dans le monôme.
- Partie littérale : correspond à toutes les variables qui forment le monôme avec tous ses exposants.
- Degré : est la somme de tous les exposants des variables monômes.
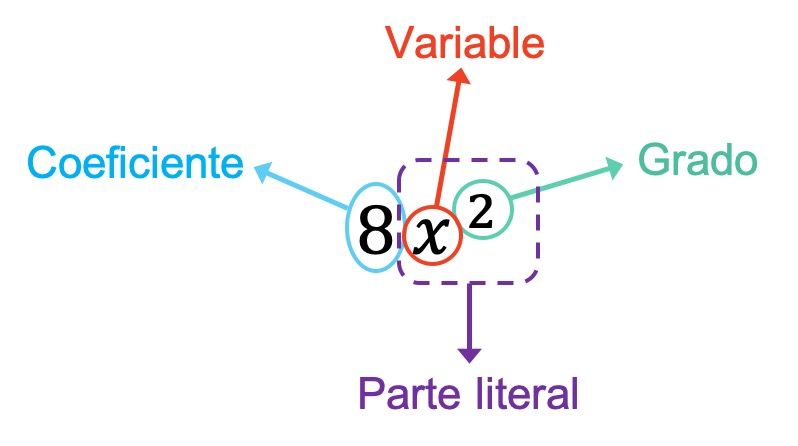
Comme vous pouvez le voir dans l’exemple précédent, le coefficient du monôme est 8 puisque c’est le nombre qui multiplie les variables. De plus, dans ce cas, le monôme n’a qu’une seule variable, qui est x. Par conséquent, la partie littérale du monôme est formée par cette variable plus son exposant, c’est-à-dire x 2 . Et enfin, le monôme est du second degré car le seul exposant qu’il a est 2.
D’autre part, l’une des propriétés des parties d’un monôme est que lorsque deux monômes ont la même partie littérale, on dit qu’ils sont des monômes similaires . Vous pouvez en savoir plus sur ce type de monômes sur la page liée, où, entre autres, il est expliqué pourquoi ils sont si importants pour les mathématiques.
Exemples de parties de monômes
Afin que vous compreniez parfaitement le concept des parties d’un monôme, nous vous laissons avec plusieurs exemples :
Exemple 1
- Coefficient du monôme :
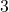
- Variables du monôme :
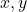(dans ce cas, il y a deux variables) - Partie littérale du monôme :
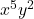
- Degré du monôme :
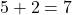
Exemple 2
- Coefficient du monôme :
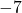
- Variables du monôme :
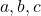(dans ce cas, il y a trois variables) - Partie littérale du monôme :
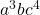
- Degré du monôme :
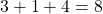
Gardez à l’esprit que lorsque l’exposant d’une variable n’est pas mis, cela signifie qu’il est élevé à un et, par conséquent, en réalité, l’exposant de cette variable est 1 et non 0. Pour cette raison, nous avons ajouté une unité dans le calcul du degré de ce monôme (3+ 1 +4=8), puisque
Si vous êtes plus intéressé, dans le lien suivant, vous pouvez voir plus d’exemples de monômes . De plus, vous pourrez voir les différents types de monômes qui existent, comment la valeur numérique d’un monôme est calculée et quelle est la différence entre un monôme et un polynôme.
Problèmes résolus des parties de monômes
Enfin, nous vous proposons plusieurs exercices afin que vous puissiez vérifier que vous avez bien compris les différentes définitions des parties d’un monôme.
Exercice 1
Quelles sont toutes les parties du monôme suivant ?
Coefficient du monôme :
Variables du monôme :
Partie littérale du monôme :
Degré du monôme :
Exercice 2
Identifiez tous les éléments du monôme suivant :
Coefficient du monôme :
Variables du monôme :
Partie littérale du monôme :
Degré du monôme :
Exercice 3
Déterminez les parties du monôme suivant avec une fraction :
Coefficient du monôme :
Variables du monôme :
Partie littérale du monôme :
Degré du monôme :
Parfait! Si vous êtes arrivé jusqu’ici, vous comprenez sûrement déjà tout sur les parties d’un monôme. C’est pourquoi vous êtes prêt à passer au niveau suivant et à apprendre à faire des opérations avec des monômes . Ici, vous verrez non seulement comment tous les types d’opérations avec des monômes qui existent sont calculés, mais vous verrez également comment résoudre des opérations combinées avec des monômes et vous pourrez vous entraîner avec des exercices résolus étape par étape.