Monômes similaires

Vous trouverez ici l’explication de ce que sont les monômes similaires. De plus, vous pourrez voir des exemples de monômes similaires et même vous entraîner avec des exercices résolus de ce type de monômes.

Quels sont les monômes similaires ?

Évidemment, pour comprendre la signification de monômes similaires, vous devez d’abord savoir ce qu’est un monôme . Je vous recommande donc de jeter un œil à la page liée avant de continuer.

Ainsi, que deux monômes sont similaires signifie ce qui suit :

Les monômes similaires sont les monômes qui ont exactement la même partie littérale. Autrement dit, deux ou plusieurs monômes sont similaires lorsqu’ils sont composés des mêmes variables (lettres) et des mêmes exposants.

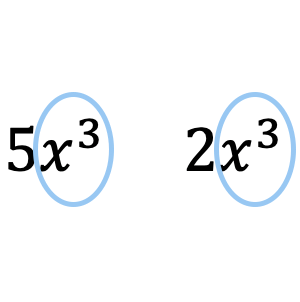
quels sont les exemples de monômes similaires

Comme vous pouvez le voir dans l’exemple ci-dessus, le monôme

$5x^3$ est semblable au monôme $2x^3$ parce qu’ils ont tous les deux la même partie littérale $(x^3),$ même si leurs coefficients sont différents.

L’une des caractéristiques des monômes similaires est qu’ils servent à la fois à additionner des monômes et à soustraire des monômes , deux opérations que vous devez maîtriser oui ou oui. Cliquez sur l’un des deux liens pour voir comment ajouter ou soustraire les monômes. De plus, dans chaque lien, vous trouverez des exemples et des exercices résolus étape par étape.

En fait, vous ne pouvez ajouter et soustraire des monômes que s’ils sont similaires. Et c’est précisément pourquoi les monômes similaires sont si importants en mathématiques.

Exemples de monômes similaires

Afin que vous puissiez bien comprendre le concept de monômes similaires, vous pouvez voir ci-dessous plusieurs exemples de monômes similaires les uns aux autres.

Exemple 1

$4x^5 \qquad -2x^5$

Les 2 monômes précédents sont similaires puisque leurs parties littérales sont équivalentes

$(x^5).$

Exemple 2

$7xy^3 \qquad 8xy^3 \qquad -6xy^3$

Les trois monômes précédents sont similaires car leurs parties littérales sont les mêmes

$(xy^3).$

Exemple 3

$12a^6b^2c^7 \qquad -4a^6b^2c^7$

$-5a^6b^2c^7 \qquad 1a^6b^2c^7$

Les quatre monômes précédents sont similaires les uns aux autres car leurs parties littérales sont identiques

$(a^6b^2c^7).$

Exercice résolu de monômes similaires

Associez les paires de monômes qui se ressemblent :

$\begin{array}{lcl} 4x^2 & \qquad \qquad & 2a^5x^6z \\[3ex]-3a^5x^6z & \qquad \qquad & 6x^2y^3z^6w^2 \\[3ex] 9y^3x & \qquad \qquad & 2xy^3 \\[3ex]4x^2y^3z^6w^2& \qquad \qquad & x^2 \end{array}$

voir solution

Les monômes similaires sont ceux qui ont les mêmes parties littérales. Par conséquent, les paires de monômes similaires sont :

$4x^2 \quad \longleftrightarrow \quad x^2$

$-3a^5x^6z\quad \longleftrightarrow \quad 2a^5x^6z$

$9y^3x\quad \longleftrightarrow \quad 2xy^3$

$4x^2y^3z^6w^2\quad \longleftrightarrow \quad 6x^2y^3z^6w^2$

Bien que cela signifie quelque chose de complètement différent, si vous êtes arrivé jusqu’ici, vous êtes probablement également intéressé à savoir en quoi consiste la décomposition polynomiale d’un nombre . Comme c’est quelque chose que très peu de gens connaissent, mais c’est en fait très utile pour simplifier les expressions mathématiques.