▷ Comment calculer la valeur numérique d'un polynôme

Sur cette page vous découvrirez ce que c’est et comment calculer la valeur numérique d’un polynôme. De plus, vous pourrez voir des exemples et des exercices résolus étape par étape de la valeur numérique d’un polynôme.

Quelle est la valeur numérique d’un polynôme ?

En mathématiques, la valeur numérique d’un polynôme P(x) pour la valeur x=a, c’est-à-dire P(a), est le résultat obtenu en remplaçant la variable x du polynôme par le nombre a et en effectuant les calculs indiqués dans l’expression polynomiale.

Afin que vous puissiez mieux comprendre le concept de valeur numérique d’un polynôme, nous montrons ci-dessous comment elle est calculée avec un exemple :

Comment calculer la valeur numérique d’un polynôme

Maintenant que nous connaissons la définition mathématique de la valeur numérique d’un polynôme, voyons comment déterminer la valeur numérique d’un polynôme à l’aide d’un exemple :

Quelle est la valeur numérique du polynôme suivant pour x=2 ?

$P(x)=x^3+5x^2-4x+1$

Pour trouver la valeur numérique du polynôme, il faut évaluer ledit polynôme dans la valeur donnée par le problème, c’est-à-dire qu’il faut substituer la variable

$x$ du polynôme par la valeur de l’énoncé. Par conséquent, dans ce cas, nous devons remplacer la lettre $x$ Pour 2:

$P(2)=2^3+5\cdot 2^2-4\cdot 2+1$

Et une fois que nous avons substitué la valeur dans l’expression algébrique du polynôme, nous effectuons les opérations. Nous résolvons donc d’abord les puissances :

$P(2)=8+5\cdot 4-4\cdot 2+1$

Maintenant, nous calculons les multiplications :

$P(2)=8+20-8+1$

Et enfin, on ajoute et soustrait les termes :

$\bm{P(2)=21}$

En conclusion, la valeur numérique du polynôme pour x=2 est égale à 21.

Comme vous pouvez le constater, trouver la valeur numérique d’un polynôme n’est pas très compliqué, mais cela a des applications très utiles. Par exemple, savoir trouver la valeur numérique d’un polynôme est essentiel pour pouvoir utiliser le théorème des restes, un théorème très important sur les polynômes. Cliquez sur ce lien et découvrez ce qu’est le théorème des restes , vous y trouverez son explication, des exemples d’utilisation et des exercices résolus étape par étape.

Exemples de valeurs numériques de polynômes

Pour que vous compreniez comment obtenir la valeur numérique d’un polynôme, nous vous laissons avec d’autres exemples résolus :

Exemple 1

Calculer la valeur numérique du polynôme 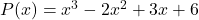$P(x)=x^3-2x^2+3x+6$ pour $x=-1.$

$\begin{aligned} P(-1) & =(-1)^3-2\cdot (-1)^2+3\cdot (-1)+6 \\[2ex] & = -1-2\cdot 1+3\cdot (-1)+6 \\[2ex] & =-1-2-3+6 \\[2ex]&= \bm{0} \end{aligned}$

Dans ce cas, la valeur numérique du polynôme est égale à 0. Cela a des conséquences dues aux propriétés des polynômes, puisque grâce au théorème des facteurs nous pouvons savoir quel sera le reste de certaines divisions entre polynômes. Pour en savoir plus, cliquez sur le lien précédent, où nous expliquons ce qu’est ce théorème et à quoi il sert.

Exemple 2

Déterminer la valeur numérique du polynôme 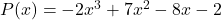$P(x)=-2x^3+7x^2-8x-2$ pour $x=3.$

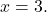
$\begin{aligned} P(3) & =-2\cdot 3^3+7\cdot 3^2-8\cdot 3-2 \\[2ex] & =-2\cdot 27+7\cdot 9-8\cdot 3-2 \\[2ex] & =-54+63-24-2 \\[2ex]&= \bm{-17} \end{aligned}$

Jusqu’à présent nous n’avons vu que comment déterminer la valeur numérique d’un polynôme de manière classique, mais il faut savoir qu’il existe une autre méthode. Plus précisément, vous pouvez également calculer la valeur numérique d’un polynôme avec la méthode Ruffini . Vous devez également savoir comment utiliser cette procédure, nous vous recommandons donc de consulter son explication détaillée dans le lien.

Valeur numérique d’un polynôme avec deux variables ou plus

Nous venons de voir comment trouver la valeur numérique d’un polynôme lorsqu’il possède une seule variable. Mais… comment obtenir la valeur numérique d’un polynôme lorsqu’il a plus d’une variable ?

Eh bien, si un polynôme a 2 lettres ou plus, sa valeur numérique doit être calculée de la même manière, c’est -à-dire remplacer d’abord chaque variable du polynôme par sa valeur correspondante, puis résoudre les opérations polynomiales .

A titre d’exemple, vous avez un problème de ce type résolu ci-dessous :

Trouver la valeur numérique du polynôme multivarié 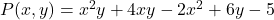$P(x,y)=x^2y+4xy-2x^2+6y-5$ pour les valeurs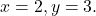 $x=2, y=3.$

Tout d’abord, nous remplaçons chaque variable par sa valeur correspondante, c’est-à-dire que nous remplaçons la lettre

$x$ pour 2 et on change la lettre $y$ par 3 :

$P(2,3)=2^2\cdot 3+4\cdot 2\cdot 3-2\cdot 2^2+6\cdot 3-5$

On résout les puissances :

$P(2,3)=4\cdot 3+4\cdot 2\cdot 3-2\cdot 4+6\cdot 3-5$

Maintenant, nous calculons les produits :

$P(2,3)=12+24-8+18-5$

Et enfin, on fait les additions et soustractions :

$\bm{P(2,3)=41}$

Ainsi, la valeur numérique du polynôme pour les données de l’instruction est équivalente à 41.

Exercices résolus sur la valeur numérique d’un polynôme

Exercice 1

Quelle est la valeur numérique du polynôme P(x) pour x=-2 ?

$P(x)=-2x^3-4x^2+3x+8$

Voir la solution

Pour trouver la valeur numérique du polynôme, nous devons simplement substituer la valeur donnée dans l’énoncé dans l’expression polynomiale et résoudre les opérations résultantes :

$\begin{aligned} P(-2) & =-2\cdot (-2)^3-4\cdot (-2)^2+3\cdot (-2)+8 \\[2ex] & =-2\cdot (-8)-4\cdot 4+3\cdot (-2)+8 \\[2ex] & =+16-16-6+8 \\[2ex]&= \bm{2} \end{aligned}$

Exercice 2

Calculez la valeur numérique du polynôme suivant avec des fractions pour x=4.

$P(x)=\cfrac{1}{2} x^2-\cfrac{5}{4}x + 7$

Voir la solution

Que le polynôme comporte ou non des fractions, la procédure pour trouver la valeur numérique du polynôme est toujours la même. Il faut donc remplacer la variable x par 4 et résoudre les calculs :

$\begin{aligned} P(4) & =\cfrac{1}{2} \cdot 4^2-\cfrac{5}{4}\cdot 4+ 7 \\[2ex] & =\cfrac{1}{2} \cdot 16-\cfrac{5}{4}\cdot 4+ 7\\[2ex] & =8-5+7 \\[2ex]&= \bm{10} \end{aligned}$

Exercice 3

Déterminer la valeur numérique du polynôme pour les valeurs x=3, y=5 et z=-2

$P(x,y,z)=x^2yz+4y^2z^2-3x^2z+6xyz$

Voir la solution

Pour déterminer la valeur numérique du polynôme multivarié, il suffit de substituer les valeurs données dans le problème dans l’expression algébrique et de résoudre les opérations résultantes :

$\begin{aligned} P(3,5,-2) & =3^2\cdot 5\cdot (-2)+4\cdot 5^2\cdot (-2)^2-3\cdot 3^2\cdot (-2)+6\cdot 3\cdot 5 \cdot (-2) \\[2ex] & =9\cdot 5\cdot (-2)+4\cdot 25\cdot 4-3\cdot 9\cdot (-2)+6\cdot 3\cdot 5 \cdot (-2) \\[2ex] & =-90+400+54-180\\[2ex]&= \bm{184} \end{aligned}$

Exercice 4

Étant donné le polynôme

$P(x)= -2x^3-3x^2+5x+k$ calculer la valeur du paramètre $k$ pour que $P(-2)=5.$

Voir la solution

Dans ce problème, pour trouver la valeur de l’inconnue

$k$ nous devons résoudre l’équation $P(-2)=5.$

$P(-2)=5$

Par conséquent, nous essayons d’abord de calculer la valeur de P(-2) :

$\begin{aligned} P(-2) & =-2\cdot (-2)^3-3\cdot (-2)^2+5\cdot (-2)+k \\[2ex] & =-2\cdot (-8)-3\cdot 4+5\cdot (-2)+k \\[2ex] & =+16-12-10+k\\[2ex]&=-6+k \end{aligned}$

Maintenant on égalise l’expression obtenue à 5 :

$P(-2)=5$

$-6+k=5$

Et pour finir, nous résolvons l’équation résultante :

$k=5+6$

$\bm{k=11}$

Quelle est la valeur numérique d’un polynôme ?

Comment calculer la valeur numérique d’un polynôme

Exemples de valeurs numériques de polynômes

Exemple 1

Exemple 2

Valeur numérique d’un polynôme avec deux variables ou plus

Exercices résolus sur la valeur numérique d’un polynôme

Exercice 1

Exercice 2

Exercice 3

Exercice 4

Leave a Comment Cancel Reply