Triangle de Tartaglia (ou de Pascal)

Sur cette page, nous expliquons ce qu’est le triangle de Tartaglia, également appelé triangle de Pascal. Nous apprenons à construire mathématiquement le triangle de Tartaglia (ou de Pascal), ainsi qu’à quoi il sert et quelles sont toutes ses propriétés. Enfin, nous montrons comment et quand ce triangle très important est né.

Qu’est-ce que le triangle de Tartaglia (ou de Pascal) ?

Le triangle de Tartaglia , également appelé triangle de Pascal , est une représentation mathématique d’entiers ordonnés sous la forme d’un triangle. Le triangle de Tartaglia (ou Pascal) est utilisé pour faire des calculs mathématiques.

C’est la définition du triangle de Tartaglia ou de Pascal, mais vous comprenez sûrement mieux le concept avec une image du triangle :

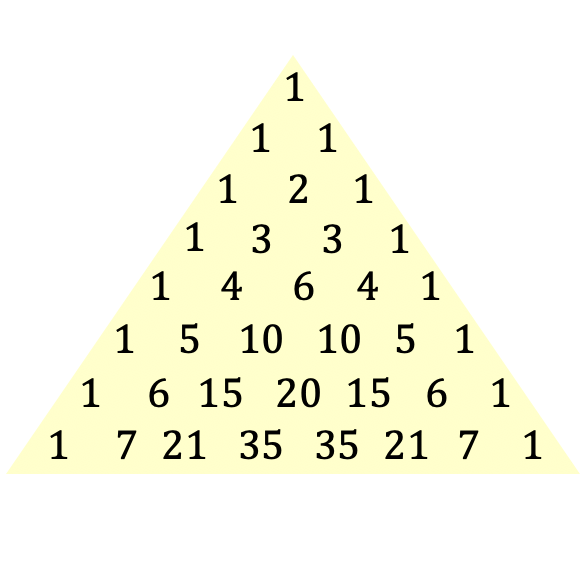
Le triangle de Tartaglia est aussi appelé triangle de Pascal d’après le philosophe et mathématicien français Blaise Pascal, qui a introduit cette expression triangulaire en 1654, bien que ce triangle soit déjà connu depuis l’Antiquité. Ci-dessous, nous allons plonger dans l’histoire de ce triangle particulier.

Comment est construit le triangle de Tartaglia ou de Pascal ?

Comme vous l’avez vu dans le triangle de Pascal (ou Tartaglia), il y a beaucoup de nombres, mais cela ne signifie pas que nous devons les connaître par cœur (Dieu merci). Il existe une formule qui permet de trouver facilement tous les nombres du triangle de Pascal ou de Tartaglia, il suffit de résoudre des sommes simples.

Pour construire le triangle Tartaglia ou Pascal, vous commencez par le haut du triangle, qui est toujours un 1, puis les lignes ci-dessous sont calculées. Chaque nombre dans les lignes suivantes correspond à la somme des deux nombres directement au-dessus, sauf les extrémités des lignes qui sont toujours 1.

Par conséquent, vous pouvez calculer autant de lignes du triangle de Tartaglia que vous le souhaitez, car vous pouvez ajouter successivement des lignes en additionnant les nombres.

A quoi sert le triangle de Tartaglia ou de Pascal ?

Savoir construire le triangle de Tartaglia c’est très bien, mais… à quoi sert ce triangle arithmétique ? Eh bien, le triangle de Tartaglia (ou de Pascal) a de nombreuses applications en mathématiques, en particulier dans le domaine de l’algèbre.

nombres combinatoires

Tout d’abord, le triangle de Tartaglia sert à calculer directement les nombres combinatoires , aussi appelés coefficients binomiaux. Si vous ne savez pas quels sont ces types d’opérations, vous pouvez les rechercher sur notre site Web (nous avons un moteur de recherche en haut à droite) car nous avons écrit un article détaillé où nous expliquons comment elles sont résolues et vous y trouverez retrouvez également des exemples et des exercices résolus pas à pas. Mais en résumé, l’expression algébrique d’un nombre combinatoire est la suivante :

$\displaystyle \begin{pmatrix} n \\ k \end{pmatrix}$

Eh bien, tous les nombres combinatoires peuvent être facilement déterminés avec le triangle de Tartaglia, car la solution de chaque coefficient binomial est équivalente à un nombre de cette expression triangulaire comme le montre la figure suivante :

nombres combinatoires du triangle de tartaglia ou de pascal

Par exemple, le nombre combinatoire

$\displaystyle \begin{pmatrix} 4 \\ 2 \end{pmatrix}$ renvoie 6, car dans le triangle de Tartaglia, il y a un 6 à la place.

Donc, si vous savez comment construire le triangle de Tartaglia ou de Pascal, vous pouvez calculer n’importe quel nombre combinatoire rapidement et sans utiliser leur formule.

binôme de Newton

Une autre utilisation du triangle de Tartaglia (ou de Pascal) est de pouvoir calculer des puissances de binômes (cliquez sur ce lien pour savoir ce qu’est un binôme).

Un exemple de la potentialisation d’un binôme sont des identités notables, telles que:

$(a+b)^2$

Les identités remarquables sont très importantes pour les mathématiques, car elles nous permettent de sauvegarder de nombreux calculs et de résoudre des opérations compliquées directement et rapidement. C’est pourquoi nous vous recommandons de consulter le lien suivant si vous ne savez toujours pas ce que sont les identités notables .

Comme vous l’avez vu dans le lien précédent, les produits notables peuvent être résolus directement avec leurs formules. Mais… que se passe-t-il lorsque le binôme est élevé au cube ou à un degré supérieur ?

$\begin{array}{c} (a+b)^3 = \ ? \\[3ex] (a+b)^4 = \ ? \\[3ex] (a+b)^5 = \ ? \\[3ex] \bm{\vdots} \end{array}$

Eh bien, ces binômes peuvent être calculés de manière très simple avec le triangle de Tartaglia grâce au théorème du binôme (ou binôme de Newton). Bien qu’une fois maîtrisée la méthode elle soit rapide à appliquer, pour bien l’expliquer il faut une page entière. Donc, si vous êtes plus intéressé par la façon de résoudre ce type de binômes, cliquez sur la page liée et vous pourrez voir comment cela se fait.

Combinatoire

Le triangle de Tartaglia, ou triangle de Pascal, peut également être utilisé pour déterminer des combinaisons et des probabilités.

Si jamais nous rencontrons un problème où nous devons déterminer combien de groupes différents peuvent être constitués d’un groupe quel que soit l’ordre, nous pouvons utiliser le triangle de Tartaglia.

Par exemple, si nous avons 5 cartes, pour savoir combien de façons nous pouvons en choisir 3, il suffit d’aller à la troisième colonne (la première colonne est zéro) de la cinquième rangée (la première rangée est aussi la rangée 0) du triangle de Tartaglia. Le nombre à cette position (10) correspond au nombre de possibilités qu’il y a de choisir 3 cartes.

$1 \quad 5 \quad 10 \quad \color{blue}\boxed{ \color{black}10} \color{black} \quad 5 \quad 1$

Ainsi, à partir de 5 cartes, 10 groupes différents de trois cartes peuvent être formés.

Propriétés du triangle de Tartaglia ou de Pascal

Le triangle de Tartaglia, aussi appelé triangle de Pascal, a les caractéristiques suivantes :

Le triangle Tartaglia (ou Pascal) est symétrique, c’est-à-dire que la ligne verticale qui divise tout le triangle en deux triangles équilatéraux égaux est un axe de symétrie.

La somme horizontale de tous les nombres de n’importe quelle ligne du triangle de Pascal équivaut à une puissance de 2.

propriétés du triangle de tartaglia ou de pascal

Les diagonales du triangle de Tartaglia sont également importantes : les nombres sur la première diagonale (diagonale externe) sont des uns, la deuxième diagonale est formée par la séquence de tous les nombres naturels, la troisième diagonale correspond aux nombres triangulaires et la quatrième diagonale est composée des nombres tétragonaux (ou tétraédriques).

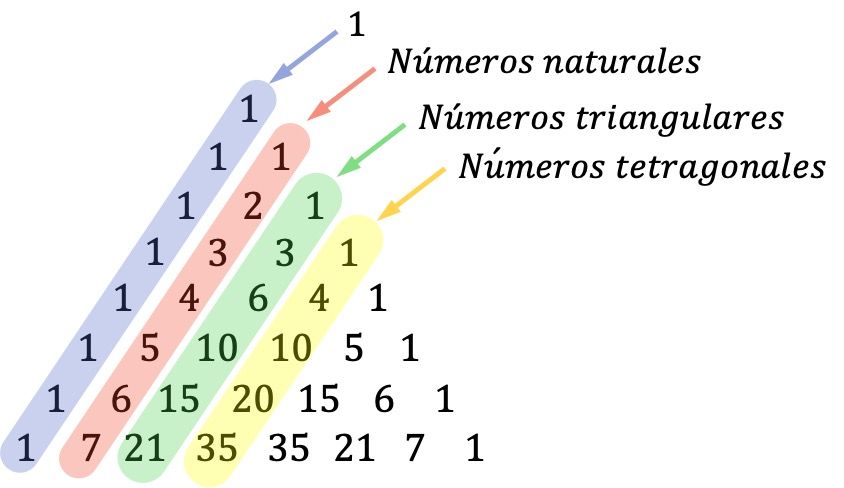
tartaglia triangle ou pascal nombres triangulaires et tétragonaux

Les nombres triangulaires sont des nombres qui peuvent être représentés sous la forme d’un triangle. Et les nombres tétragonaux sont ceux qui forment des pyramides triangulaires.

Si vous ne savez pas ce que sont les nombres triangulaires ou tétragonaux, rien ne se passe, c’est juste une curiosité sur le triangle de Tartaglia. Cependant, vous devez connaître la signification des nombres naturels (nombres utilisés pour compter les éléments).

À l’exception du nombre 1, si le premier nombre d’une ligne est un nombre premier, tous les nombres de cette même ligne sont divisibles par ce nombre. Par exemple, dans la huitième rangée (1-7-21-35-35-21-7-1), les nombres 7, 21 et 35 peuvent être divisés par 7 (sept est un nombre premier).

Une autre particularité du triangle de Tartaglia est que la série de Fibonacci peut être trouvée en additionnant les diagonales d’une certaine manière :

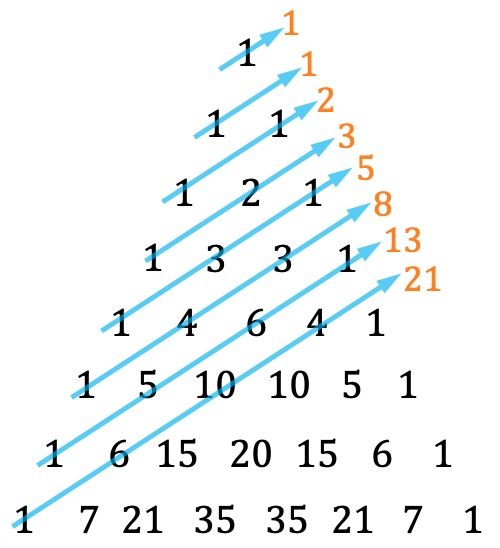
tartaglia ou triangle pascal série de fibonacci

Rappelons que chaque terme de la suite de Fibonacci est égal à la somme des deux précédents, les deux premiers termes étant 1 et 1. Ainsi les nombres qui appartiennent à la suite de Fibonacci sont : 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233,…

Si on additionne deux nombres consécutifs de la troisième diagonale du triangle de Pascal (1-3-6-10-15-…) on obtient un carré parfait (1, 4, 9, 16, 25,…).

Si nous peignons les nombres pairs du triangle de Pascal dans une couleur et les nombres impairs dans une autre couleur, nous obtenons la figure du triangle de Sierpinski, un célèbre ensemble géométrique. Ci-dessous, vous pouvez voir le triangle de Pascal d’une hauteur de 512 représenté avec les nombres impairs colorés en noir et les nombres pairs colorés en blanc :

triangle sierpinski de tataglia ou triangle pascal

La conjecture de Singmaster dit que le nombre de fois que chaque nombre supérieur à 1 se produit est fini. Ou en d’autres termes, bien que le nombre de rangées dans le triangle de Tartaglia soit infini, le nombre de fois où chaque nombre apparaît sauf 1 est fini. Par curiosité, le nombre 3003 est le seul connu à ce jour à apparaître jusqu’à huit fois dans le triangle.

Histoire du triangle de Tartaglia ou Pascal

Maintenant que nous savons à quoi ressemble le triangle de Tartaglia, voyons quand ce triangle mathématique très spécial a été inventé.

Bien que le nom du triangle arithmétique soit principalement attribué aux célèbres scientifiques Tartaglia et Pascal, ce triangle algébrique était déjà utilisé auparavant.

Le premier enregistrement d’un triangle formé par des coefficients binomiaux date du 10ème siècle en Inde. Cependant, les Perses commencèrent à étudier ses propriétés, notamment les mathématiciens Al-Karaji (953-1029) et Omar Khayyam (1048-1131). C’est pourquoi en Iran, il a été popularisé sous le nom de triangle Khayyam-Pascal ou même simplement de triangle Khayyam .

Ce triangle a commencé à être introduit en Chine au 11ème siècle par le mathématicien Jia Xian, mais c’est plus tard au 13ème siècle que Yang Hui l’a présenté sous le nom de triangle arithmétique . Et pour cette raison, dans le pays asiatique, ils l’appellent le triangle Yang Hui .

Le triangle mathématique a atteint le continent européen plus tard à travers l’allemand Petrus Apianus, spécifiquement publié en l’an 1527 dans son livre Rechnung . De là, le célèbre algébriste italien Niccolò Fontana Tartaglia a étudié le triangle en profondeur au cours de la première moitié du XVIe siècle, et en son honneur dans des pays comme l’Italie, il est connu sous le nom de triangle de Tartaglia.

Enfin, le Français Blaise Pascal a démontré nombre des propriétés du triangle étudiées dans sa publication du Traité du triangle arithmétique en 1654, d’où le nom de triangle de Pascal. Il convient de noter que certaines de ces propriétés étaient déjà connues, mais c’est Pascal qui a réalisé leur démonstration par induction mathématique.