Sur cette page, nous expliquons comment soustraire des polynômes. De plus, vous trouverez plusieurs exemples et exercices résolus pas à pas de soustraction de polynômes.
Comment soustraire des polynômes ?
Pour soustraire deux polynômes, il faut soustraire les termes des polynômes qui sont semblables. Autrement dit, la soustraction de polynômes consiste à soustraire les termes qui ont la même partie littérale (mêmes variables et mêmes exposants).
En mathématiques, vous pouvez calculer la soustraction de polynômes de deux manières différentes : avec la méthode verticale ou avec la méthode horizontale. Vous trouverez ci-dessous l’explication des deux procédures, mais nous vous conseillons d’abord d’apprendre à soustraire des polynômes verticalement, puis de passer à la méthode horizontale. Bien évidemment restez avec celui que vous préférez.
Soustraction de polynômes verticaux
Ensuite, nous allons voir comment deux polynômes sont soustraits verticalement à l’aide d’un exemple :
- faire la soustraction
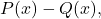étant les deux polynômes :
La première chose que nous devons faire pour trouver une soustraction polynomiale est de placer un polynôme sous l’autre, de sorte que les termes similaires des deux polynômes soient alignés par colonnes :
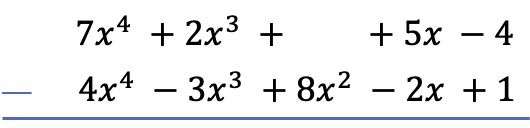
Attention : Si un polynôme n’a pas de terme d’un certain degré, il faut laisser l’espace vide. Par exemple, le polynôme
n’a pas de monôme du second degré, il y a donc un espace vide à sa place.
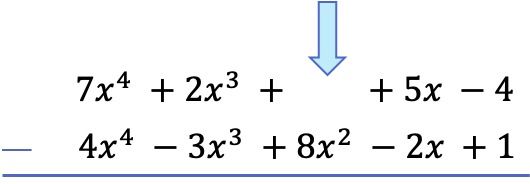
Bien que nous puissions maintenant soustraire directement les polynômes, il est assez facile de se tromper de signe si nous procédons de cette façon. Par conséquent, pour soustraire des polynômes, il est préférable de changer le signe de tous les termes du polynôme de soustraction (le polynôme de soustraction) puis de faire l’addition. Puisque soustraire un polynôme équivaut à ajouter son polynôme opposé.
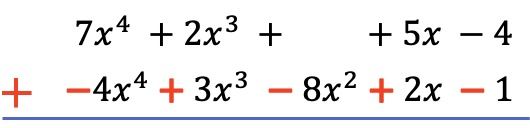
Et une fois que nous avons classé tous les termes dans l’ordre du degré le plus élevé au degré le plus bas et que nous avons nié les termes du polynôme ci-dessous, nous ajoutons les coefficients de chaque colonne en gardant les parties littérales égales :
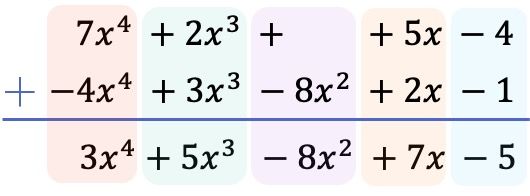
Par conséquent, le résultat obtenu à partir de la soustraction des 2 polynômes est :
Au cas où la dernière étape ne vous serait pas claire, je vous laisse avec l’explication de comment se fait l’ addition de polynômes , en effet il est indispensable que vous maîtrisiez l’addition de polynômes pour pouvoir bien soustraire des polynômes. Sur la page liée, vous trouverez également des exemples et des exercices résolus d’addition de polynômes et, en plus, vous pourrez voir les différences entre l’addition et la soustraction de polynômes.
Soustraction de polynômes horizontaux
Nous venons de voir comment soustraire des polynômes verticalement, mais maintenant nous allons voir l’autre méthode qui existe pour soustraire des polynômes : soustraire des polynômes horizontalement. Cette procédure est sûrement plus rapide que la précédente, cependant il est nécessaire d’avoir une maîtrise supérieure des concepts de polynômes.
Voyons donc en quoi consiste cette méthode de soustraction de polynômes à travers un exemple. Et pour que vous puissiez voir les différences entre les deux méthodes, nous allons soustraire les mêmes polynômes que dans l’exemple précédent :
- Calculer le reste 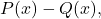étant les deux polynômes :
Il faut tout d’abord mettre les deux polynômes sous la forme d’une opération algébrique, c’est-à-dire l’un après l’autre :
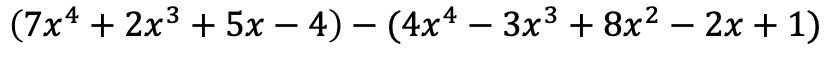
Les monômes de la première parenthèse restent les mêmes, par contre les termes de la deuxième parenthèse doivent changer de signe car ils ont un négatif devant :
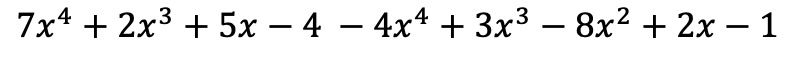
Et maintenant, nous regroupons les termes qui ont des parties littérales identiques, c’est-à-dire les termes avec les mêmes variables (lettres) et les mêmes exposants. Les termes qui ne sont pas similaires ne peuvent pas être ajoutés ou soustraits.
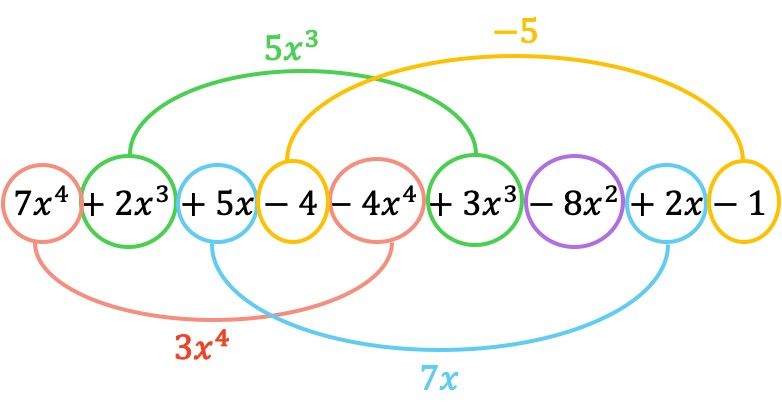
Donc le polynôme résultant de la soustraction est :
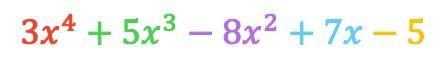
Comme vous pouvez le voir, nous avons obtenu le même résultat avec les deux méthodes, vous pouvez donc utiliser celle qui vous convient le mieux.
Maintenant que vous avez vu les 2 méthodes pour résoudre la soustraction polynomiale, saviez-vous que vous pouvez également soustraire des fractions avec des polynômes ? Et pas seulement des soustractions, mais toutes sortes d’opérations. Découvrez comment se font les opérations avec les fractions algébriques en cliquant sur ce lien.
Problèmes résolus de la soustraction de polynômes
Afin que vous puissiez vous entraîner, nous vous laissons plusieurs exercices résolus de soustraction de polynômes. Si vous avez des questions sur un exercice vous pouvez le poser dans les commentaires de la page, nous y répondrons dans les plus brefs délais.
Exercice 1
Soustraire le polynôme
moins le polynôme 
Dans ce cas, nous soustrairons les deux polynômes verticalement. Pour ce faire, on ordonne d’abord les polynômes par degré, puis on change le signe des termes polynomiaux restants et, enfin, on ajoute les monômes situés dans la même colonne :
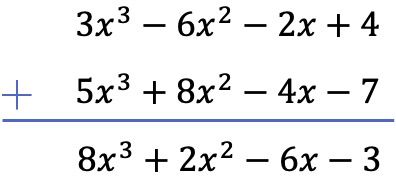
Exercice 2
Résoudre le polynôme de soustraction
moins le polynôme
Soustraire deux polynômes revient à ajouter au polynôme diminutif l’opposé du polynôme soustrait. Par conséquent, nous changeons le signe des termes du polynôme sous-traitant (celui qui reste) et ajoutons les polynômes :
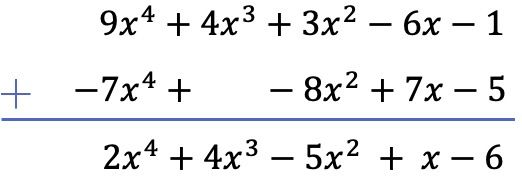
Remarquez que dans ce cas particulier un espace vide doit être laissé dans la colonne de degré 3 du deuxième polynôme, puisqu’il n’a pas de terme de troisième degré.
Exercice 3
Trouver le résultat de la soustraction du polynôme
moins le polynôme
Dans ce cas, nous résoudrons la soustraction des deux polynômes verticalement. Donc, d’abord, nous mettons les polynômes dans l’ordre du plus grand au plus petit degré, puis nous changeons le signe des termes du polynôme restant et, enfin, nous ajoutons les termes similaires :
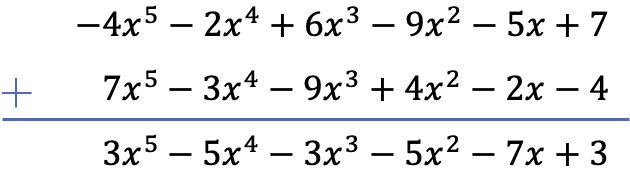
Exercice 4
Calculez l’opération suivante avec des polynômes :
Dans ce cas, 3 polynômes sont impliqués dans l’opération, dont 2 sont des soustractions. Par conséquent, pour résoudre l’opération, nous allons changer le signe de tous les termes des deux polynômes restants, puis nous additionnerons les polynômes.
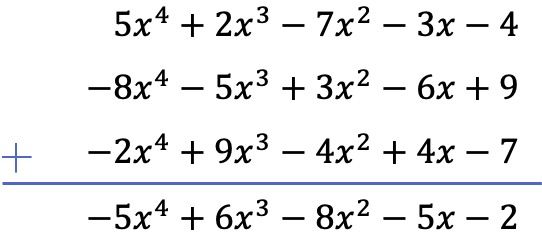
Qu’avez-vous pensé de l’explication ? L’avez-vous trouvé utile ? Quelle méthode de soustraction de polynômes préférez-vous, la verticale ou l’horizontale ? On vous lit dans les commentaires ! 👀
