Dans cet article, nous expliquons ce qu’est la périodicité d’une fonction. De plus, vous verrez plusieurs exemples de fonctions périodiques. Enfin, nous analyserons la période des fonctions trigonométriques, car c’est l’une de ses caractéristiques les plus importantes.
Qu’est-ce que la périodicité d’une fonction ?
La périodicité d’une fonction est une caractéristique des fonctions qui répètent leurs valeurs de manière cyclique, c’est-à-dire qu’une fonction est périodique si son graphique se répète à chaque certain intervalle. Cet intervalle s’appelle une période.
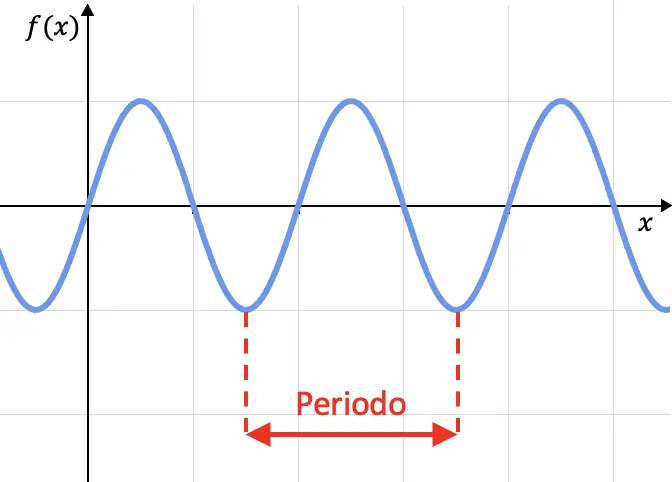
Mathématiquement, une fonction est définie comme périodique si elle est remplie que
![]() pour toute valeur de la variable indépendante x.
pour toute valeur de la variable indépendante x.
![]()
Où T est la période de la fonction périodique i k tout entier.
Exemples de périodicités de fonctions
Une fois que nous avons vu le concept de périodicité d’une fonction, nous allons voir plusieurs exemples de comment calculer la périodicité d’une fonction.
Exemple 1
Déterminez si la fonction suivante est périodique :
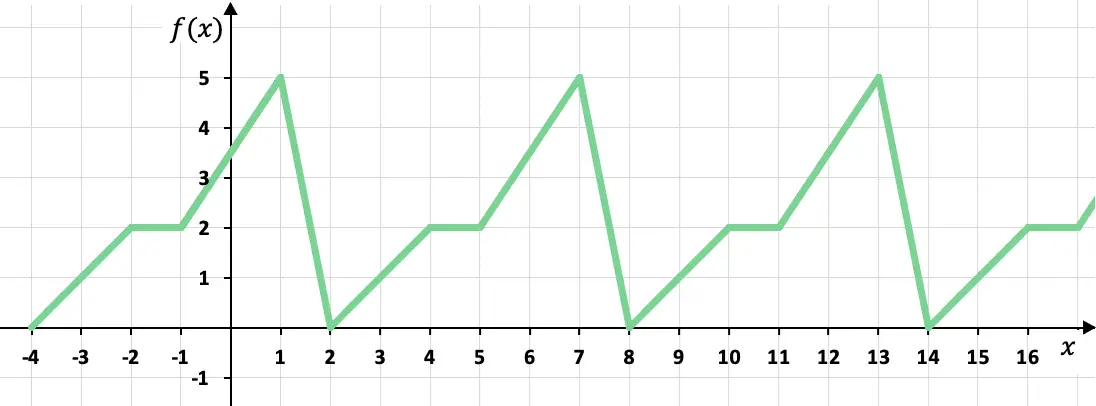
Cette fonction définie par morceaux est une fonction périodique, puisque les valeurs de son graphe se répètent cycliquement. Plus précisément, la fonction prend la même valeur tous les six x, par conséquent, la période de la fonction est égale à 6.
![]()
Exemple 2
Trouver la périodicité de la fonction suivante :
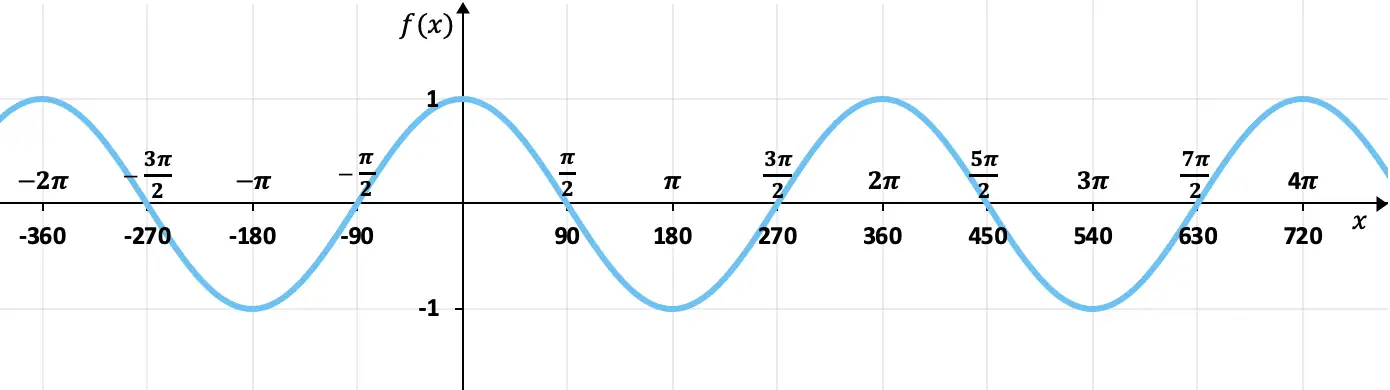
Cette fonction correspond à la représentation graphique d’une fonction trigonométrique, plus précisément la fonction cosinus.
Comme nous pouvons le voir sur le graphique, la fonction répète ses valeurs périodiquement, c’est donc une fonction périodique. De plus, entre le pic et le pic de l’onde, il y a un espace de 2π (ou 360º), c’est donc la période de la fonction.
![]()
Périodicité des fonctions trigonométriques
La périodicité et les fonctions trigonométriques sont étroitement liées, en fait, l’une des principales caractéristiques de ce type de fonctions est que la plupart des fonctions trigonométriques sont périodiques.
Ensuite, nous allons étudier la périodicité des 3 principales fonctions trigonométriques : le sinus, le cosinus et la tangente.
Période de la fonction sinus
L’expression de la fonction sinus est la suivante :
![]()
Dans ce cas, il n’est pas nécessaire de représenter graphiquement la fonction pour trouver sa période, mais on peut la calculer simplement en appliquant la formule suivante :
![]()
De plus, la fonction sinus a la particularité que si nous modifions sa période, nous changeons également la forme de son graphique. Vous pouvez voir comment la valeur de la période affecte sa représentation graphique dans le lien suivant :
➤ Voir : Graphique de la fonction sinus
Période de la fonction cosinus
L’expression algébrique de la fonction cosinus est la suivante :
![]()
Comme pour le sinus, la période de la fonction cosinus peut être trouvée directement à l’aide de la formule suivante :
![]()
La valeur de la période du cosinus conditionne complètement son graphique, cliquez sur le lien suivant et découvrez pourquoi :
➤ Voir : Graphique de la fonction cosinus
Période de la fonction tangente
La fonction tangente est décrite mathématiquement :
![]()
La période de la fonction tangente est calculée avec la même formule que celle du sinus et du cosinus :
![]()
Cependant, le graphique de la fonction tangente est différent du sinus et du cosinus, car il a également des asymptotes qui se répètent périodiquement. Vous pouvez voir cela et d’autres fonctionnalités de cette fonction trigonométrique sur le lien suivant :
➤ Voir : Graphique de la fonction tangente