▷ Qu'est-ce que c'est et comment est calculé un nombre combinatoire (exemples)

Sur cette page, nous expliquons ce qu’est un nombre combinatoire et comment il est calculé (formule). De plus, vous pourrez voir des exemples sur la façon de calculer n’importe quel nombre combinatoire et vous entraîner avec des exercices résolus étape par étape. Nous montrons également toutes les propriétés et applications des nombres combinatoires. Et enfin, nous apprenons comment trouver le résultat d’un nombre combinatoire directement avec la calculatrice.

Qu’est-ce qu’un nombre combinatoire ?

En mathématiques, le nombre combinatoire , également appelé coefficient binomial, est le nombre de combinaisons ordinaires (combinaisons sans répétition) de groupes de k éléments pouvant être formés à partir d’un ensemble de n éléments (n>k).

Un nombre combinatoire s’exprime entre parenthèses comme suit :

$\begin{pmatrix}n \\ k \end{pmatrix}$

En revanche, le nombre combinatoire se lit n sur k . De même, n est appelé le numérateur et k est appelé l’ordre.

Rien qu’avec la définition d’un nombre combinatoire, il est difficile de comprendre sa signification. Cependant, nous allons maintenant voir comment le nombre combinatoire est déterminé mathématiquement, puis nous approfondirons ce concept de combinatoire. Vous verrez que de cette façon vous le comprendrez mieux.

Formule de nombre combinatoire

La formule qui permet de calculer la valeur d’un nombre combinatoire (ou coefficient binomial) est la suivante :

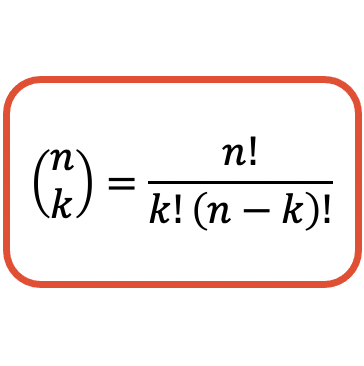
Rappelons qu’en algèbre le point d’exclamation correspond à la factorielle d’un nombre. Et pour trouver la factorielle d’un nombre, vous devez multiplier tous les entiers positifs de 1 par ce nombre. Par exemple, pour calculer la factorielle du nombre 4 il faut multiplier 1, 2, 3 et 4 :

$4! = 1\cdot 2 \cdot 3 \cdot 4 =24$

Il est également important que vous sachiez que la factorielle de 0 est égale à 1.

$0! = 1$

Exemple de calcul d’un nombre combinatoire

Ensuite, nous allons déterminer étape par étape la valeur d’un nombre combinatoire à titre d’exemple, afin que vous puissiez voir comment cela se fait :

Calculez la valeur du nombre combinatoire de 5 sur 3.

Le coefficient binomial de 5 sur 3 correspond à l’expression suivante :

$\begin{pmatrix}5 \\ 3 \end{pmatrix}$

Par conséquent, si nous appliquons la formule des nombres combinatoires, pour déterminer sa valeur, nous devons effectuer les opérations suivantes :

$\begin{pmatrix}5 \\ 3 \end{pmatrix} = \cfrac{5!}{3!(5-3)!}$

Ou équivalent:

$\begin{pmatrix}5 \\ 3 \end{pmatrix} = \cfrac{5!}{3!\cdot 2!}$

On retrouve donc les factorielles :

$\begin{pmatrix}5 \\ 3 \end{pmatrix} = \cfrac{1\cdot 2 \cdot 3 \cdot 4 \cdot 5}{(1\cdot 2 \cdot 3) \cdot (1\cdot 2)}$

La multiplication 1·2·3 est répétée au numérateur et au dénominateur, la fraction peut donc être simplifiée en éliminant ce facteur :

$\begin{pmatrix}5 \\ 3 \end{pmatrix} = \cfrac{\cancel{1\cdot 2 \cdot 3} \cdot 4 \cdot 5}{(\cancel{1\cdot 2 \cdot 3)} \cdot (1\cdot 2)}$

$\begin{pmatrix}5 \\ 3 \end{pmatrix} = \cfrac{ 4 \cdot 5}{1\cdot 2}$

Maintenant, nous calculons les produits :

$\begin{pmatrix}5 \\ 3 \end{pmatrix} = \cfrac{20}{2}$

Et enfin, on fait la division :

$\begin{pmatrix}5 \\ 3 \end{pmatrix} = \bm{10}$

Propriétés du nombre combinatoire

Les nombres combinatoires, ou coefficients binomiaux, peuvent être combinés selon les propriétés suivantes :

Deux nombres combinatoires complémentaires sont ceux qui ont le même numérateur n et la somme de leurs ordres est équivalente audit numérateur. Ainsi, le résultat de deux nombres combinatoires complémentaires est identique.

$\begin{pmatrix}n \\ k \end{pmatrix} = \begin{pmatrix}n \\ n-k \end{pmatrix}$

Cette caractéristique des nombres combinatoires est également appelée identité de symétrie.

Par exemple, 6 sur 4 donne le même résultat que 6 sur 2, car 6-4=2.

$\begin{pmatrix}6 \\ 4 \end{pmatrix} =\cfrac{6!}{4!(6-4)!} = \cfrac{\cancel{1\cdot 2 \cdot 3\cdot 4}\cdot 5 \cdot 6}{(\cancel{1\cdot 2 \cdot 3\cdot 4})\cdot (1\cdot 2)}= \cfrac{30}{2} = \bm{15}$

$\begin{pmatrix}6 \\ 2 \end{pmatrix} =\cfrac{6!}{2!(6-2)!} = \cfrac{\cancel{1\cdot 2 \cdot 3\cdot 4}\cdot 5 \cdot 6}{(1\cdot 2)\cdot (\cancel{1\cdot 2 \cdot 3\cdot 4})}= \cfrac{30}{2} = \bm{15}$

La somme de deux nombres combinatoires de même numérateur et d’ordres successifs est égale à un autre nombre combinatoire dont le numérateur est équivalent au numérateur des additions plus 1 et dont l’ordre correspond à la plus grande valeur des ordres des additions. Autrement dit, la condition suivante est toujours remplie :

$\begin{pmatrix}n\\ k \end{pmatrix} + \begin{pmatrix}n\\ k+1 \end{pmatrix}= \begin{pmatrix}n+1\\ k+1 \end{pmatrix}$

Par exemple:

$\begin{pmatrix}9\\ 2 \end{pmatrix} + \begin{pmatrix}9\\ 3 \end{pmatrix}= \begin{pmatrix}10\\ 3 \end{pmatrix}$

Cette propriété est également connue sous le nom de règle de Pascal.

D’autre part, cette formule peut également être appliquée à l’inverse pour décomposer un nombre combinatoire en deux nombres combinatoires plus simples :

$\begin{pmatrix}n\\ k \end{pmatrix} = \begin{pmatrix}n-1\\ k-1 \end{pmatrix}+ \begin{pmatrix}n-1\\ k \end{pmatrix}$

Par exemple, le nombre combinatoire 8 sur 4 est égal à 7 sur 3 plus 7 sur 4 :

$\begin{pmatrix}8\\ 4 \end{pmatrix} = \begin{pmatrix}7\\ 3 \end{pmatrix}+ \begin{pmatrix}7\\ 4 \end{pmatrix}$

Tout nombre positif supérieur à 1 est égal au nombre lui-même.

$\begin{pmatrix}n\\ 1 \end{pmatrix} =n$

La raison de cette propriété est que la factorielle d’un nombre est égale à la factorielle du nombre précédent multipliée par le nombre lui-même :

$\begin{pmatrix}n \\ 1 \end{pmatrix} =\cfrac{n!}{1!(n-1)!} = \cfrac{n\cdot (n-1) \cdot (n-2)\cdots 1}{(n-1) \cdot (n-2)\cdots 1}= n$

Exemples de ce type de nombres combinatoires :

$\begin{pmatrix}12\\ 1 \end{pmatrix} =12 \qquad \begin{pmatrix}5\\ 1 \end{pmatrix} =5 \qquad \begin{pmatrix}9\\ 1 \end{pmatrix} =9$

Tout nombre positif supérieur à 0 est égal à un.

$\begin{pmatrix}n\\ 0 \end{pmatrix} =1$

En effet, le dénominateur de la fraction d’un tel nombre combinatoire sera toujours égal au numérateur de la fraction :

$\begin{pmatrix}n\\ 0 \end{pmatrix} =\cfrac{n!}{0!(n-0)!} =\cfrac{n!}{n!} = 1$

Exemples de nombres combinatoires comme celui-ci :

$\begin{pmatrix}6\\ 0 \end{pmatrix} =1 \qquad \begin{pmatrix}2\\ 0 \end{pmatrix} =1 \qquad \begin{pmatrix}23\\ 0 \end{pmatrix} =1$

Chaque nombre sur lui-même est égal à 1.

$\begin{pmatrix}n\\ n \end{pmatrix} =1$

Voici la démo :

$\begin{pmatrix}n\\ n \end{pmatrix} =\cfrac{n!}{n!(n-n)!} =\cfrac{n!}{n!\cdot 0!}= \cfrac{n!}{n!} = 1$

Exemples de nombres combinatoires comme celui-ci :

$\begin{pmatrix}5\\ 5 \end{pmatrix} =1 \qquad \begin{pmatrix}37\\ 37 \end{pmatrix} =1 \qquad \begin{pmatrix}14\\ 14 \end{pmatrix} =1$

Comment calculer un nombre combinatoire avec la calculatrice

Jusqu’à présent, nous avons vu comment trouver un nombre combinatoire de nombres plus ou moins simples, mais lorsque nous devons opérer avec de très grandes quantités, il est préférable d’utiliser la calculatrice pour déterminer le nombre combinatoire. Nous allons maintenant voir comment introduire un nombre combinatoire dans la calculatrice.

Ainsi, la clé utilisée pour calculer un nombre combinatoire avec la calculatrice est la clé nCr . Et pour déterminer la valeur du nombre combinatoire, il faut d’abord saisir le numérateur du nombre combinatoire, dans un deuxième temps appuyer sur la touche nCr, puis saisir l’ordre du nombre combinatoire et enfin appuyer sur la touche égale.

$\begin{pmatrix}n\\ k \end{pmatrix}\quad \color{red}\bm{\longrightarrow} \quad \color{black} n \rightarrow \boxed{nCr} \rightarrow k \rightarrow \boxed{=}$

Sur les calculatrices scientifiques CASIO, la touche nCr possède généralement son propre bouton ou se trouve au-dessus du bouton de division, selon le modèle.

Par exemple, si nous voulons savoir ce que vaut le nombre combinatoire 10 sur 6, nous devons faire la séquence suivante :

$\begin{pmatrix}10\\ 6 \end{pmatrix}\quad \color{red}\bm{\longrightarrow} \quad \color{black} 10 \rightarrow \boxed{nCr} \rightarrow 6 \rightarrow \boxed{=} \rightarrow 210$

Applications du nombre combinatoire

Si vous êtes arrivé jusqu’ici, vous savez sûrement déjà comment résoudre n’importe quel nombre combinatoire, parfait. Mais… à quoi sert le nombre combinatoire ? Eh bien, nous verrons ensuite tous les avantages que présente ce type d’opération très spéciale.

Combinatoire

Comme nous l’avons vu en début de page, le résultat d’un nombre combinatoire

$\begin{pmatrix}n\\ k \end{pmatrix}$ représente le nombre de groupes possibles de $k$ éléments qui peuvent être constitués à partir d’un ensemble d’un total de $n$ articles.

Par conséquent, certains problèmes combinatoires peuvent être résolus grâce à des nombres combinatoires (ou coefficients binomiaux). Voyons comment procéder à l’aide d’un exemple :

Dans une classe de 30 élèves, nous souhaitons choisir un groupe composé de 4 élèves pour réaliser certaines tâches. Quel est le nombre total de groupes différents pouvant être constitués ?

Dans ce cas, l’ordre des élèves n’a pas d’importance, le même élève ne se répète pas deux fois au sein du groupe, et tous les élèves n’entrent pas dans le groupe. Par conséquent, la formule des nombres combinatoires peut être utilisée pour déterminer de combien de façons le groupe peut être constitué.

Pour ce faire, il faut calculer le nombre combinatoire avec le nombre total d’élèves comme numérateur et avec le nombre d’élèves qui formeront le groupe comme ordre :

$\begin{pmatrix}30 \\ 4 \end{pmatrix} =\cfrac{30!}{4!(30-4)!} =\cfrac{30\cdot 29 \cdot 28 \cdot 27 \cdot \cancel{26!}}{4\cdot 3 \cdot 2 \cdot 1 \cdot \cancel{26!}} = \cfrac{657720}{24}=\bm{27405}$

Le nombre total de combinaisons possibles est donc de 27 405 groupes.

Binôme de Newton

Une autre application des nombres combinatoires est le binôme de Newton. Le binôme de Newton est un polynôme composé de deux termes élevés ensemble à un nombre entier, c’est-à-dire que le binôme de Newton est ce polynôme qui répond à l’expression algébrique suivante :

$(a+b)^n$

Évidemment, si le binôme est au carré, cela signifie qu’il s’agit d’une identité notable et, par conséquent, il peut être facilement calculé avec la formule correspondante. En revanche, lorsque le binôme est élevé à de grands nombres, le calcul devient assez difficile. Eh bien, le théorème binomial de Newton dit que ces types de polynômes peuvent être calculés très facilement à partir de nombres combinatoires.

Cliquez sur le lien suivant et découvrez ce qu’est la formule binomiale de Newton et comment elle est calculée. De plus, vous pourrez voir des exemples et vous entraîner avec des exercices résolus étape par étape. Et enfin, vous découvrirez la curieuse histoire de ce théorème.

Le triangle de Tartaglia (ou de Pascal)

Comme vous l’avez vu tout au long de cet article, calculer manuellement le coefficient binomial de grands nombres peut être laborieux et compliqué.

En revanche, avec le triangle de Tartaglia, également appelé triangle de Pascal, tous les nombres combinatoires peuvent être déterminés facilement grâce à une règle mnémotechnique. C’est logiquement très utile puisque cela permet de gagner beaucoup de temps lors des calculs.

Pour savoir exactement comment procéder, consultez l’explication du triangle de Tartaglia . Sur cette page liée, vous découvrirez ce qu’est ce mystérieux triangle, à quoi il sert (il a des applications surprenantes) 😮 et quelle est son origine (il était déjà utilisé il y a plus de 1000 ans).

Exercices résolus de nombres combinatoires

Afin que vous puissiez pratiquer et bien comprendre les concepts expliqués, nous vous laissons plusieurs exercices résolus étape par étape sur les nombres combinatoires.

Exercice 1

Trouvez le nombre combinatoire 9 sur 5 (sans utiliser de calculatrice).

Voir la solution

Pour trouver la valeur du nombre combinatoire 9 sur 5 on applique simplement la formule factorielle :

$\begin{pmatrix}9 \\ 5 \end{pmatrix} =\cfrac{9!}{5!(9-5)!} = \cfrac{9\cdot 8 \cdot 7\cdot 6\cdot \cancel{5!}}{\cancel{5!} \cdot (4 \cdot 3 \cdot 2 \cdot 1)}= \cfrac{3024}{24} = \bm{126}$

Exercice 2

Quel est le résultat de la somme suivante de deux nombres combinatoires ? (sans calculatrice)

$\begin{pmatrix}10\\ 6 \end{pmatrix} + \begin{pmatrix}10\\ 7 \end{pmatrix}$

Voir la solution

Des propriétés des nombres combinatoires, il s’ensuit que la somme du problème est égale au nombre combinatoire suivant :

$\begin{pmatrix}10\\ 6 \end{pmatrix} + \begin{pmatrix}10\\ 7 \end{pmatrix}=\begin{pmatrix}11\\ 7 \end{pmatrix}$

Par conséquent, il suffit de calculer le nombre combinatoire 11 sur 7 :

$\begin{pmatrix}11 \\ 7 \end{pmatrix} =\cfrac{11!}{7!(11-7)!} = \cfrac{11\cdot 10 \cdot 9\cdot 8 \cdot \cancel{7!}}{\cancel{7!} \cdot (4 \cdot 3 \cdot 2 \cdot 1)}= \cfrac{7920}{24} = \bm{330}$

Exercice 3

Déterminez si les nombres combinatoires suivants sont égaux :

$\begin{pmatrix}6\\ 0 \end{pmatrix} \qquad \begin{pmatrix}6\\ 1 \end{pmatrix}\qquad \begin{pmatrix}6\\ 6 \end{pmatrix}$

Voir la solution

Pour trouver le résultat des trois nombres combinatoires, vous n’avez pas besoin d’utiliser une calculatrice, mais ils peuvent être facilement trouvés grâce aux propriétés des nombres combinatoires.

Tout d’abord, un nombre combinatoire de n’importe quel nombre supérieur à 0 donne 1. Par conséquent :

$\begin{pmatrix}6\\ 0 \end{pmatrix} =1$

D’un autre côté, tout nombre supérieur à l’unité est égal au nombre lui-même. Pourtant:

$\begin{pmatrix}6\\ 1 \end{pmatrix} =6$

Et enfin, tout nombre combinatoire formé par le même nombre répété deux fois est équivalent à 1. Donc :

$\begin{pmatrix}6\\ 6 \end{pmatrix} =1$

En conclusion, les premier et troisième nombres combinatoires du problème sont égaux, cependant, ils sont différents du nombre combinatoire du milieu.

$\begin{pmatrix}6\\ 0 \end{pmatrix}= \begin{pmatrix}6\\ 6 \end{pmatrix}\neq \begin{pmatrix}6\\ 1 \end{pmatrix}$

Nombre combinatoire (ou coefficient binomial)

Qu’est-ce qu’un nombre combinatoire ?

Formule de nombre combinatoire

Exemple de calcul d’un nombre combinatoire

Propriétés du nombre combinatoire

Comment calculer un nombre combinatoire avec la calculatrice

Applications du nombre combinatoire

Combinatoire

Binôme de Newton

Le triangle de Tartaglia (ou de Pascal)

Exercices résolus de nombres combinatoires

Exercice 1

Exercice 2

Exercice 3

Leave a Comment Cancel Reply