Matrice involutive

Sur cette page, vous apprendrez ce qu’est une matrice involutive. Nous vous montrons également des exemples de matrices involutives de dimension 2×2, 3×3 et 4×4. Et enfin, vous trouverez la formule d’une matrice involutive.

Qu’est-ce qu’une matrice involutive ?

La signification de matrice involutive est la suivante :

Définition de matrice involutive : Une matrice carrée inversible dont la matrice inverse est la matrice elle-même.

$A^{-1} = A$

Où

$A$ est une matrice quelconque et $A^{-1}$ représente son inverse.

Alors évidemment une matrice involutive est un exemple de matrice régulière ou non dégénérée .

Si vous ne savez pas ce qu’est l’inverse d’une matrice, vous pouvez voir ici comment calculer la matrice inverse 3×3 . Il est important de savoir comment inverser une matrice, cependant, pour cela, vous devez également savoir comment l’ adjoint d’une matrice est calculé.

Mais revenons au sujet : lorsqu’une matrice est involutive, la multiplication de la matrice par la matrice elle-même donne la matrice identité. Jetez un œil à la démo :

Toute matrice multipliée par son inverse donne la matrice Identité (ou Unité). Donc:

$\displaystyle A \cdot A^{-1} = I$

Et puisque l’inverse d’une matrice involutive est la matrice elle-même :

$\displaystyle A \cdot A = I$

Par conséquent, une matrice involutive élevée au carré donne la matrice identité :

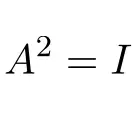
Exemples de matrices involutives

Exemple de matrice involutive 2×2 :

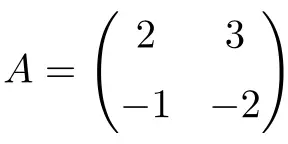
exemple de matrice involutive de dimension 2x2

On peut vérifier qu’il s’agit d’une matrice involutive en calculant la seconde puissance de la matrice :

$\displaystyle A^2=\begin{pmatrix} 2 & 3 \\[1.1ex] -1 & -2 \end{pmatrix} \cdot \begin{pmatrix} 2 & 3 \\[1.1ex] -1 & -2 \end{pmatrix}= \begin{pmatrix} 1 & 0 \\[1.1ex] 0 & 1 \end{pmatrix}$

Puisque la matrice A au carré est la matrice identité, la matrice A est une matrice involutive 2×2.

Exemple de matrice involutive 3×3 :

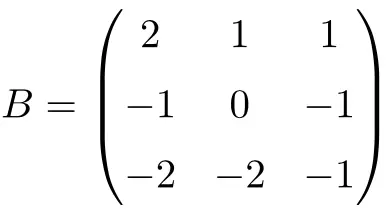
exemple de matrice involutive de dimension 3x3

On peut vérifier qu’il s’agit d’une matrice involutive en résolvant le produit de la matrice par lui-même :

$\displaystyle B^2=\begin{pmatrix} 2 & 1 & 1 \\[1.1ex] -1 & 0 & -1 \\[1.1ex] -2 & -2 & -1 \end{pmatrix}\cdot \begin{pmatrix} 2 & 1 & 1 \\[1.1ex] -1 & 0 & -1 \\[1.1ex] -2 & -2 & -1 \end{pmatrix}= \begin{pmatrix} 1 & 0 & 0 \\[1.1ex] 0 & 1 & 0 \\[1.1ex] 0 & 0 & 1 \end{pmatrix}$

Puisque la matrice B au carré est la matrice identité, la matrice B est une matrice involutive 3×3.

Exemple de matrice involutive 4×4 :

La matrice Identité (ou Unité), quelle que soit sa dimension, est par définition une matrice involutive.

$\displaystyle I=\begin{pmatrix} 1 & 0 & 0 & 0 \\[1.1ex]0 & 1 & 0 & 0\\[1.1ex]0 & 0 & 1 & 0 \\[1.1ex]0 & 0 & 0 & 1 \end{pmatrix}$

On peut vérifier qu’il s’agit d’une matrice involutive en élevant la matrice à 2 :

$\displaystyle I^2=\begin{pmatrix} 1 & 0 & 0 & 0 \\[1.1ex]0 & 1 & 0 & 0\\[1.1ex]0 & 0 & 1 & 0 \\[1.1ex]0 & 0 & 0 & 1 \end{pmatrix}\cdot \begin{pmatrix} 1 & 0 & 0 & 0 \\[1.1ex]0 & 1 & 0 & 0\\[1.1ex]0 & 0 & 1 & 0 \\[1.1ex]0 & 0 & 0 & 1 \end{pmatrix}= \begin{pmatrix} 1 & 0 & 0 & 0 \\[1.1ex]0 & 1 & 0 & 0\\[1.1ex]0 & 0 & 1 & 0 \\[1.1ex]0 & 0 & 0 & 1 \end{pmatrix}$

Puisque la matrice identité au carré est la matrice identité, la matrice identité est une matrice involutive 4×4.

Évidemment, la matrice d’identité peut être de n’importe quelle dimension, puisqu’il s’agit simplement d’une matrice diagonale avec tous les 1 sur la diagonale principale et le reste 0. Ainsi, la matrice d’identité sera toujours une matrice involutive, quel que soit son ordre.

Formule matricielle involutive

Une des propriétés de la matrice involutive est que sa formule peut être connue. Mais la preuve de la formule d’une matrice involutive du second ordre est assez fastidieuse, nous allons donc vous laisser directement sur le résultat, c’est ce qui est vraiment important. Si vous êtes plus intéressé par la démo, vous pouvez la voir expliquée étape par étape ci-dessous dans les commentaires.

La formule d’une matrice involutive de dimension 2 × 2 est la suivante :

Par conséquent, toute matrice dont les valeurs de la diagonale principale sont opposées et dont le déterminant est -1, sera une matrice involutive.

Cependant, en plus des matrices décrites par cette formule, il faut tenir compte du fait que la matrice identité et son contraire sont aussi des matrices involutives d’ordre 2 :

$\displaystyle \begin{pmatrix} 1 & 0 \\[1.1ex] 0 & 1 \end{pmatrix} \qquad \begin{pmatrix} -1 & 0 \\[1.1ex] 0 & -1 \end{pmatrix}$

Propriétés d’une matrice involutive

Les matrices involutives ont les caractéristiques suivantes :

Le déterminant d’une matrice involutive est toujours égal à -1 ou +1.

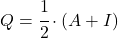Il existe une relation entre les matrices involutives et les matrices idempotentes : la matrice $A$ est involutive si et seulement si la matrice $\displaystyle Q= \cfrac{1}{2} \cdot (A+I)$ est idempotent.

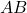Ouais $A$ et $B$ sont deux matrices involutives commutant , alors le produit matriciel $AB$ est aussi une autre matrice involutive.

Toute puissance d’une matrice involutive aboutit à une autre matrice involutive. En particulier, une matrice involutive élevée à un exposant impair sera égale à elle-même, par contre si elle est élevée à un exposant pair elle sera équivalente à la matrice Identité.

$A^2 = I$

$A^3 = A$