Proprietà dei determinanti

In questa sezione vedremo quali sono tutte le proprietà dei determinanti . Inoltre dimostriamo ciascuna proprietà con un esempio in modo che tu possa comprenderla completamente. Inoltre troverai esercizi relativi alle proprietà dei determinanti.

Di seguito spiegheremo ciascuna proprietà dei determinanti una per una, ma se preferisci puoi passare direttamente alla tabella riassuntiva sottostante. 😉

Proprietà 1: Determinante della matrice trasposta

Il determinante di una matrice è equivalente al determinante della sua matrice trasposta.

\lvert A \rvert = \lvert A^t \rvert

Esempio:

\lvert A \rvert = \begin{vmatrix} 2 & 3 \\[1.1ex] 1 & 5 \end{vmatrix} = 2 \cdot 5 - 1 \cdot 3 = 10 - 3 = \bm{7}

Ora trasponiamo la matrice 2×2 e risolviamo il determinante. Notiamo che otteniamo lo stesso risultato di prima:

\lvert A^t \rvert = \begin{vmatrix} 2 & 1 \\[1.1ex] 3 & 5 \end{vmatrix} = 2 \cdot 5 - 3 \cdot 1 = 10 - 3 = \bm{7}

Proprietà 2: Determinante con una riga o una colonna riempita di zeri

Se un determinante ha una riga o una colonna piena di zeri, il determinante restituisce 0.

\displaystyle \begin{vmatrix} a_{11} & 0 & a_{13} \\[1.1ex] a_{21} & 0 & a_{23} \\[1.1ex] a_{31} & 0 & a_{33}\end{vmatrix}=0

Esempio:

\begin{vmatrix} 5 & 6 & 2 \\[1.1ex] 0 & 0 & 0 \\[1.1ex] -3 & 1 & 4 \end{vmatrix} = \bm{0} \qquad \qquad \begin{vmatrix} 1 & -5 & 0 \\[1.1ex] 6 & 2 & 0 \\[1.1ex] 1 & 3 & 0 \end{vmatrix} = \bm{0}

In entrambi questi esempi, i determinanti valgono 0. Perché la seconda riga del primo determinante è tutta zero e anche la terza colonna del secondo determinante è tutta zero.

Proprietà 3: Determinante con due righe o colonne uguali

Se un determinante ha due righe o due colonne uguali o multiple, il determinante è zero (0).

Pertanto, se esiste una combinazione lineare tra righe o colonne, cioè sono linearmente dipendenti, il determinante dà 0.

Esempio:

\begin{vmatrix} 3 & 4 & 4 \\[1.1ex] -1 & 5 & 5 \\[1.1ex] 6 & 2 & 2 \end{vmatrix} = 0

In questo caso il determinante dà 0 perché le colonne 2 e 3 sono uguali.

Proprietà 4: Modifica le righe o le colonne di un determinante

Se due righe o due colonne vengono modificate l’una rispetto all’altra, il determinante dà lo stesso risultato ma con segno diverso.

\displaystyle \begin{vmatrix} a & b & c \\[1.1ex] d & e & f \\[1.1ex] g & h & i \end{vmatrix}= - \begin{vmatrix} a & c & b \\[1.1ex] d & f & e \\[1.1ex] g & i & h \end{vmatrix}

Esempio:

\begin{vmatrix} 3 & 2 & -4 \\[1.1ex] 1 & 5 & 6 \\[1.1ex] 1 & 0 & -3 \end{vmatrix} = \displaystyle -45 +12+0+20-0+6= \bm{-7}

Ora cambiamo l’ordine delle colonne 2 e 3 l’una rispetto all’altra. Si noti che il risultato è lo stesso ma con un segno diverso:

\begin{vmatrix} 3 & -4 & 2 \\[1.1ex] 1 & 6 & 5 \\[1.1ex] 1 & -3 & 0 \end{vmatrix} = \displaystyle 0-20-6-12+45-0= \bm{+7}

Proprietà 5: Moltiplica una riga di un determinante per uno scalare

Moltiplicare tutti gli elementi di un’intera riga o colonna per un numero reale equivale a moltiplicare il risultato del determinante per quel numero.

\displaystyle \begin{vmatrix} k \cdot a_{11} & k \cdot a_{12} & k \cdot a_{13} \\[1.1ex] a_{21} & a_{22} & a_{23} \\[1.1ex] a_{31} & a_{32} & a_{33} \end{vmatrix} =k \cdot \begin{vmatrix} a_{11} & a_{12} & a_{13} \\[1.1ex] a_{21} & a_{22} & a_{23} \\[1.1ex] a_{31} & a_{32} & a_{33} \end{vmatrix}

\displaystyle \begin{vmatrix} k \cdot a_{11} & a_{12} & a_{13} \\[1.1ex] k \cdot a_{21} & a_{22} & a_{23} \\[1.1ex] k \cdot a_{31} & a_{32} & a_{33} \end{vmatrix} =k \cdot \begin{vmatrix} a_{11} & a_{12} & a_{13} \\[1.1ex] a_{21} & a_{22} & a_{23} \\[1.1ex] a_{31} & a_{32} & a_{33} \end{vmatrix}

Esempio:

\displaystyle \begin{vmatrix} 2 & 3 \\[1.1ex] 1 & 4 \end{vmatrix} = 8-3= \bm{5}

Adesso prendiamo lo stesso determinante e moltiplichiamo un’intera riga per 2. Vedrai che il risultato sarà quello del determinante precedente ma moltiplicato per 2, ovvero 10:

\displaystyle \begin{vmatrix} 2 \cdot 2 & 2 \cdot 3 \\[1.1ex] 1 & 4 \end{vmatrix} = \begin{vmatrix} 4 & 6 \\[1.1ex] 1 & 4 \end{vmatrix} = 16-6 =\bm{10}

Proprietà 6: Determinante del prodotto della matrice

Il determinante del prodotto di due matrici è uguale al prodotto del determinante di ciascuna matrice separatamente.

\displaystyle \lvert A \cdot B \rvert = \lvert A \rvert \cdot \lvert B \rvert

Esempio:

Per dimostrare questa proprietà dei determinanti, calcoleremo il determinante della moltiplicazione delle due matrici seguenti in due modi possibili:

\displaystyle A= \begin{pmatrix} 1 & 3 \\[1.1ex] 2 & 5 \end{pmatrix}\quad B=\begin{pmatrix} 4 & 2 \\[1.1ex] 1 & -1 \end{pmatrix}

Per prima cosa moltiplicheremo le due matrici, poi calcoleremo il determinante della matrice risultante:

\displaystyle \left| A \cdot B \right| =\left| \begin{pmatrix} 1 & 3 \\[1.1ex] 2 & 5 \end{pmatrix} \cdot \begin{pmatrix} 4 & 2 \\[1.1ex] 1 & -1 \end{pmatrix}\right| = \left| \begin{pmatrix} 7 & -1 \\[1.1ex] 13 & -1 \end{pmatrix} \right| = -7 - (-13) = \bm{6}

Ora calcoliamo separatamente il determinante di ciascuna matrice e poi moltiplichiamo i risultati:

\displaystyle \lvert A \rvert \cdot \lvert B \rvert = \left| \begin{pmatrix} 1 & 3 \\[1.1ex] 2 & 5 \end{pmatrix} \right| \cdot \left| \begin{pmatrix} 4 & 2 \\[1.1ex] 1 & -1 \end{pmatrix}\right| = -1\cdot (-6)= \bm{6}

Come puoi vedere, fare prima il prodotto della matrice e poi il determinante dà lo stesso risultato che facendo prima il determinante di ciascuna matrice e poi moltiplicando i risultati.

Questa condizione non si applica invece alle operazioni di addizione e sottrazione, vale a dire che il determinante della somma (o sottrazione) di due matrici non dà lo stesso risultato della somma (o sottrazione) dei determinanti di due matrici separatamente.

Proprietà 7: Determinante della matrice inversa

Se una matrice è invertibile, il determinante del suo inverso corrisponde all’inverso del determinante della matrice originale.

\displaystyle \begin{vmatrix} A^{-1} \end{vmatrix} = \cfrac{1}{\lvert A \rvert}

Esempio:

Verificheremo questa proprietà calcolando prima l’inversa di una matrice e poi risolvendo il suo determinante. Vedremo che il risultato equivale a trovare il determinante della matrice originale e invertirlo.

Invertiamo quindi la seguente matrice e calcoliamo il suo determinante:

\displaystyle A= \begin{pmatrix} 4 & 2 \\[1.1ex] 7 & 4 \end{pmatrix}

\displaystyle A^{-1}= \begin{pmatrix} 2 & -1 \\[1.1ex] -\frac{7}{2} & 2 \end{pmatrix}

\displaystyle \begin{vmatrix}A^{-1} \end{vmatrix}= \begin{vmatrix} 2 & -1 \\[1.1ex] -\frac{7}{2} & 2 \end{vmatrix} = 4-\cfrac{7}{2} =\cfrac{8}{2}-\cfrac{7}{2} = \cfrac{\bm{1}}{\bm{2}}

E ora risolviamo il determinante della matrice originale e facciamo la sua inversa:

\displaystyle \begin{vmatrix}A\end{vmatrix}= \begin{pmatrix} 4 & 2 \\[1.1ex] 7 & 4 \end{pmatrix}=16-14=2

\displaystyle \begin{vmatrix}A^{-1}\end{vmatrix}= \cfrac{\bm{1}}{\bm{2}}

Come puoi vedere, i risultati di entrambe le operazioni sono identici. La proprietà è quindi dimostrata.

Proprietà 8: Sostituisci la riga di un determinante

La riga di un determinante può essere sostituita aggiungendo (o sottraendo) la stessa riga più (o meno) un’altra riga moltiplicata per un numero.

Esempio:

Con il seguente esempio verificheremo questa proprietà. Per prima cosa calcoleremo un determinante, poi opereremo su una riga del determinante e ricalcoleremo il suo risultato. Vedrai come otteniamo lo stesso risultato in entrambi i casi.

Quindi, calcoliamo prima un determinante 3×3 con la regola di Sarrus:

\begin{vmatrix} 2 & 1 & -1 \\[1.1ex] 3 & 0 & 1 \\[1.1ex] 0 & -3 & 6 \end{vmatrix} \displaystyle=0+0+9-0+6-18 = \bm{-3}

Ora, nella riga 2, aggiungiamo la prima riga moltiplicata per 2:

\displaystyle \begin{vmatrix} 2 & 1 & -1 \\[1.1ex] 3 & 0 & 1 \\[1.1ex] 0 & -3 & 6 \end{vmatrix} \begin{matrix} \\[1.1ex] \xrightarrow{f_2 + 2f_1} \\[1.1ex] \ \end{matrix} \begin{vmatrix} 2 & 1 & -1 \\[1.1ex] 7 & 2 & -1 \\[1.1ex] 0 & -3 & 6 \end{vmatrix}

E risolviamo il determinante dopo aver trasformato una delle sue rette:

\displaystyle \begin{vmatrix} 2 & 1 & -1 \\[1.1ex] 7 & 2 & -1 \\[1.1ex] 0 & -3 & 6 \end{vmatrix} = 24+0+21-0-6-42=\bm{-3}

In entrambi i casi il risultato è stato -3. Si dimostra quindi che il risultato di un determinante non cambia se una riga viene sostituita dalla somma della stessa riga più un’altra riga moltiplicata per un numero.

Proprietà 9: Determinante di una matrice triangolare

Il determinante di una matrice triangolare è il prodotto degli elementi della sua diagonale principale.

Esempio:

Risolveremo come esempio il determinante della seguente matrice triangolare:

\begin{vmatrix} 2 & 3 & 5 \\[1.1ex] 0 & -1 & 7 \\[1.1ex] 0 & 0 & 4 \end{vmatrix} \displaystyle= 2 \cdot (-1) \cdot 4 = \bm{-8}

Proprietà 10: Determinante di una matrice diagonale

Il determinante di una matrice diagonale è pari alla moltiplicazione degli elementi della sua diagonale principale.

Esempio:

Prendiamo come esempio il determinante della seguente matrice diagonale:

\begin{vmatrix}5 & 0 & 0 \\[1.1ex] 0 & 3 & 0 \\[1.1ex] 0 & 0 & -2 \end{vmatrix} \displaystyle= 5 \cdot 3 \cdot (-2) = \bm{-30}

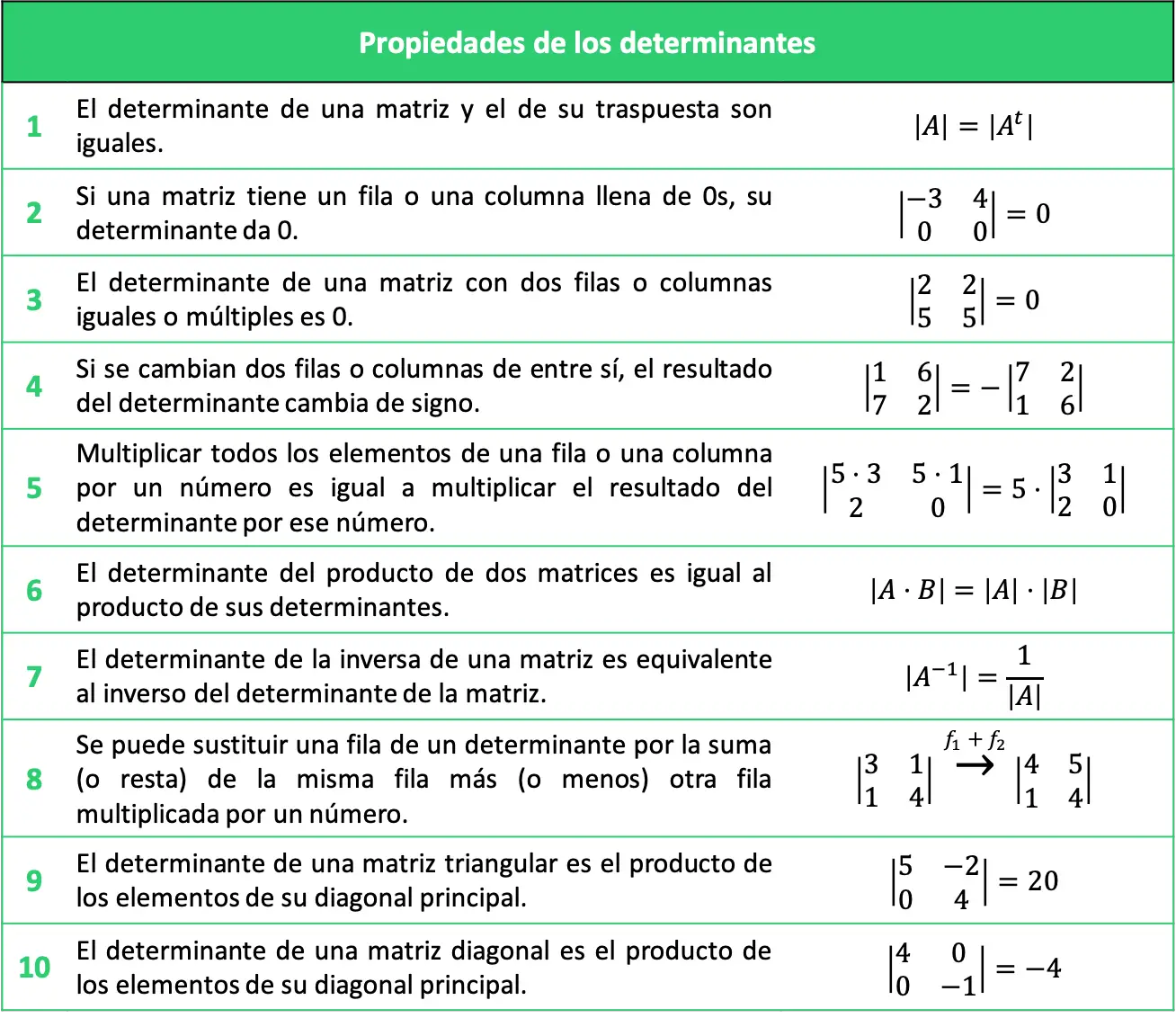
Tabella riassuntiva delle proprietà dei determinanti

Le proprietà dei determinanti spiegate possono essere riassunte nella seguente tabella:

proprietà dei determinanti

Esercizi risolti con le proprietà dei determinanti

Esercizio 1

Risolvi il seguente determinante:

\displaystyle \begin{vmatrix} 3 & 1 & 0 \\[1.1ex] 4 & 2 & 0 \\[1.1ex] -1 & 6 & 0 \end{vmatrix}

Se un determinante ha una riga o una colonna piena di zeri, il determinante restituisce 0 (proprietà 2). Pertanto, il risultato del determinante è 0, perché la terza colonna è piena di zeri.

Esercizio 2

Risolvi il seguente determinante:

\displaystyle \begin{vmatrix} 4 & 2 & -3 & 5 \\[1.1ex] 1 & 5 & 3 & 2 \\[1.1ex]4 & 2 & -3 & 5 \\[1.1ex] -2 & 0 & 4 & 3 \end{vmatrix}

Se un determinante ha due righe o due colonne uguali o multiple, il determinante restituisce 0 (proprietà 3). Pertanto, il risultato del determinante è 0, perché la prima riga e la terza riga sono uguali.

Esercizio 3

Calcolare il seguente determinante:

\displaystyle \begin{vmatrix} 1 & 0 & 2 & 2 \\[1.1ex] 3 & 1 & 5 & 6 \\[1.1ex] 1 & 3 & -2 & 2 \\[1.1ex] 2 & 2 & 0 & 4 \end{vmatrix}

Se un determinante ha due righe o due colonne uguali o multiple, il determinante restituisce 0 (proprietà 3). Pertanto, il risultato del determinante è 0, perché la quarta colonna è il doppio della prima colonna.

Esercizio 4

Conosciamo il risultato di un determinante, anche se non conosciamo gli elementi della matrice:

\displaystyle \begin{vmatrix} a & b \\[1.1ex] c & d \end{vmatrix} = 3

Dal risultato del determinante precedente e dalle proprietà dei determinanti, calcolare il risultato dei seguenti determinanti:

\displaystyle \mathbf{a} \bm{)} \ \begin{vmatrix} a & c \\[1.1ex] b & d \end{vmatrix} \qquad \mathbf{b} \bm{)} \ \begin{vmatrix} b & a \\[1.1ex] d & c \end{vmatrix} \qquad \mathbf{c} \bm{)} \ \begin{vmatrix} a & 3b \\[1.1ex] c & 3d \end{vmatrix}

Per)

\begin{pmatrix} a & c \\ b & d \end{pmatrix}

è la matrice trasposta di

\begin{pmatrix} a & b \\ c & d \end{pmatrix}

. E il determinante di una matrice è uguale al determinante della sua matrice trasposta (proprietà 1). Pertanto, anche il risultato di questo determinante è 3.

\displaystyle \begin{vmatrix} a & c \\[1.1ex] b & d \end{vmatrix}=\begin{vmatrix} a & b \\[1.1ex] c & d \end{vmatrix}=\bm{3}

b) Nella determinazione

\begin{vmatrix} b & a \\ d & c \end{vmatrix}

le colonne 1 e 2 sono state modificate rispetto alla determinante del prospetto

\begin{vmatrix} a & b \\ c & d \end{vmatrix}

. Pertanto, secondo la proprietà 4, il risultato è uguale al risultato del determinante dell’enunciato ma con segno diverso, cioè -3.

\displaystyle \begin{vmatrix} b & a \\[1.1ex] d & c \end{vmatrix} = - \begin{vmatrix} a & b \\[1.1ex] c & d \end{vmatrix}= \bm{-3}

c) Nella determinazione

\begin{vmatrix} a & 3b \\ c & 3d \end{vmatrix}

tutta la seconda colonna del determinante dell’enunciato è stata moltiplicata per 3. Pertanto dalla proprietà 5 si deduce che il suo risultato sarà anche il risultato del determinante dell’enunciato moltiplicato per 3, cioè 9.

\displaystyle \begin{vmatrix} a & 3b \\[1.1ex] c & 3d \end{vmatrix} =3 \begin{vmatrix} a & b \\[1.1ex] c & d \end{vmatrix} =3 \cdot 3 = \bm{9}

Esercizio 5

Conosciamo il risultato di questi due determinanti:

\displaystyle\vert A \vert = \begin{vmatrix} 1 & 2 & 0 & 1 \\[1.1ex] -2 & -1 & 1 & 0 \\[1.1ex] 1 & 3 & 3 & -1 \\[1.1ex] 3 & 4 & 1 & 1 \end{vmatrix}=8

\displaystyle\vert B \vert = \begin{vmatrix} 0 & 1 & 3 & 2 \\[1.1ex] -1 & -2 & 0 & 0 \\[1.1ex] 3 & 1 & 1 & 2 \\[1.1ex] -1 & 2 & 3 & 1 \end{vmatrix} = - 4

Da queste informazioni calcolare:

\displaystyle \vert A \cdot B \vert

Per calcolare il risultato del determinante non è necessario moltiplicare le matrici 4×4. Poiché il determinante del prodotto di due matrici è uguale al prodotto del determinante di ciascuna matrice separatamente (proprietà 6). Ancora:

\vert A \cdot B \vert = \vert A \vert \cdot \vert B \vert = 8 \cdot (-4) = \bm{-32}

Lascia un commento

Il tuo indirizzo email non sarà pubblicato. I campi obbligatori sono contrassegnati *

Torna in alto