Probabilmente hai sentito parlare di numeri complessi . Sono forse l’insieme di numeri più difficile da gestire, perché combinano numeri reali e immaginari. La sua unificazione rende possibile studiare comportamenti numerici che non possono essere trattati utilizzando tutti i numeri reali.
Cosa sono i numeri complessi?
I numeri complessi sono la combinazione di un numero reale e di un numero immaginario . Ad esempio, 4 + 5i è un numero complesso che ha una parte reale pari a 4 e una parte immaginaria pari a 5i. In generale possiamo esprimerli con la seguente formula:
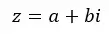
Dove Re(z) = a e Im(z) = b
Come abbiamo detto bene, i complessi sono l’ insieme più grande o insieme globale , che comprende sia numeri reali che numeri immaginari. Successivamente, ti mostriamo un piccolo diagramma della struttura gerarchica di tutti gli insiemi:

Pertanto, quando abbiamo una combinazione di un numero reale e di un numero immaginario, abbiamo un numero complesso. Ma ci sono momenti in cui una delle due parti è uguale a zero. Cosa succede in questi casi? Bene, abbiamo ancora a che fare con i complessi, perché l’insieme complesso comprende tutti gli altri insiemi numerici. Ma entriamo in una sottocategoria diversa:
| numero complesso | festa reale | parte dell’immaginazione | Sottocategoria |
| 2+5i | 2 | 5i | Complesso |
| 4 | 4 | 0 | puro reale |
| 3i | 0 | 3i | Pura immaginazione |
Quando abbiamo un reale puro, poiché il valore immaginario b è uguale a zero, il numero complesso rimanente è equivalente a:
z = un + 0i = un
Quando invece abbiamo pura immaginazione, a è uguale a zero e, di conseguenza, il numero complesso rimane il seguente:
z = 0 + bi = bi
Rappresentazione grafica dei numeri complessi
Per rappresentare i numeri complessi utilizziamo il piano complesso . Che è composta da due linee : la linea reale e la linea immaginaria. Queste due linee numeriche servono per localizzare graficamente i numeri in ogni serie e se le mettiamo insieme, otteniamo uno schema, come ad esempio:

L’asse X è chiamato asse reale perché è lì che si trovano i valori delle parti reali. Mentre l’asse Y è chiamato asse immaginario, è qui che vengono scritti i valori immaginari. Vediamo un esempio, posizioneremo il numero 3+2i nel piano complesso.

Come hai visto nell’immagine, abbiamo individuato il numero utilizzando i numeri 3 e 2 come coordinate, ciascuno per un asse. Se vuoi saperne di più sulla rappresentazione dei numeri complessi, ti consigliamo di leggere questo articolo.
Quali sono i tipi di numeri complessi?
Ora vedremo i modi a nostra disposizione per esprimere un numero complesso. Finora abbiamo visto solo la forma base (chiamata forma binomiale), che si scrive come somma: parte reale più parte immaginaria.
Ma in realtà abbiamo tre forme: la binomiale, la polare e la trigonometrica . Ogni tipo di espressione ha le sue proprietà e viene utilizzata in una situazione o nell’altra. Quindi li spiegheremo tutti e mostreremo come passare dall’uno all’altro.
1. Forma binomiale
I numeri complessi in forma binomiale si scrivono come la somma della parte reale e della parte immaginaria: a + bi. Ad esempio, il numero 6 + i è un complesso espresso in notazione binomiale. In questo caso la formula è sempre la stessa:

Pertanto, per esprimere un numero complesso in forma binomiale, è sufficiente conoscere il suo valore reale e il suo valore immaginario.
Ad esempio, il valore 3 + 2i è in forma binomiale e, come abbiamo visto in precedenza, è rappresentato così:

La forma binomiale viene utilizzata principalmente per risolvere addizioni e sottrazioni di numeri complessi.
2. Forma polare
Per esprimere i numeri complessi in forma polare , dobbiamo calcolare il loro modulo |z| e la sua argomentazione. La forma polare viene utilizzata principalmente quando dobbiamo risolvere la moltiplicazione e la divisione di numeri complessi.
Per calcolare il modulo del numero complesso, basta fare il modulo di a e b, come spiegato nella seguente formula:

E per calcolare l’argomento o l’angolo di z, dobbiamo calcolare l’arcotangente di b tra a:

È importante notare che per determinare esattamente il valore dell’angolo α è necessario individuare in quale quadrante esso si trova. Infatti, la funzione arcotangente calcola solo gli angoli compresi tra π/2 e -π/2. Per specificare in quale quadrante si trova il numero complesso, dobbiamo guardare i valori a e b (se sono positivi o negativi):
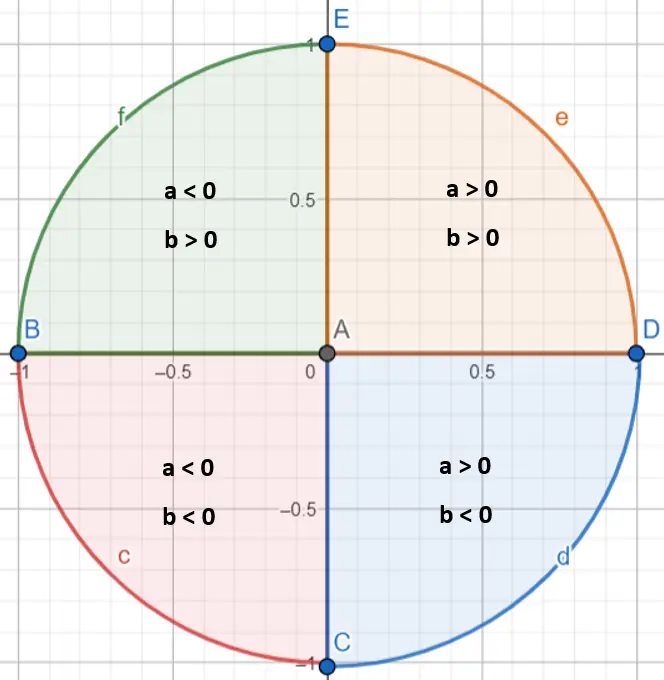
Una volta che sappiamo in quale quadrante rientra il nostro numero, dobbiamo seguire alcune regole:
- Se il numero complesso si trova nel primo quadrante (a > 0 e b > 0), lasceremo l’argomento così com’è.
- Se il numero complesso si trova nel secondo quadrante (a < 0 e b > 0), aggiungeremo π all’argomento.
- Se il numero complesso si trova nel terzo quadrante (a < 0 e b < 0), sottraiamo π dall’argomento.
- Se il numero complesso si trova nel quarto quadrante (a > 0 e b < 0), aggiungeremo 2π all’argomento.
Se non sai di cosa parliamo quando diciamo quadrante, ti consigliamo di consultare il nostro articolo sui rapporti trigonometrici .
Una volta che conosciamo il modulo e l’argomento di z, possiamo esprimere il numero complesso in forma polare. Sebbene questa forma accetti diverse nomenclature, le due principali sono:

Se, ad esempio, vogliamo cambiare il numero 3 + 5i in polare, dovremo semplicemente seguire la seguente procedura.
Per prima cosa calcoliamo il modulo:
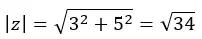
Poi calcoliamo l’argomento, che è nel primo quadrante, quindi rimane come lo abbiamo calcolato.
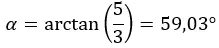
Ed esprimiamo il numero in forma polare:
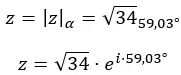
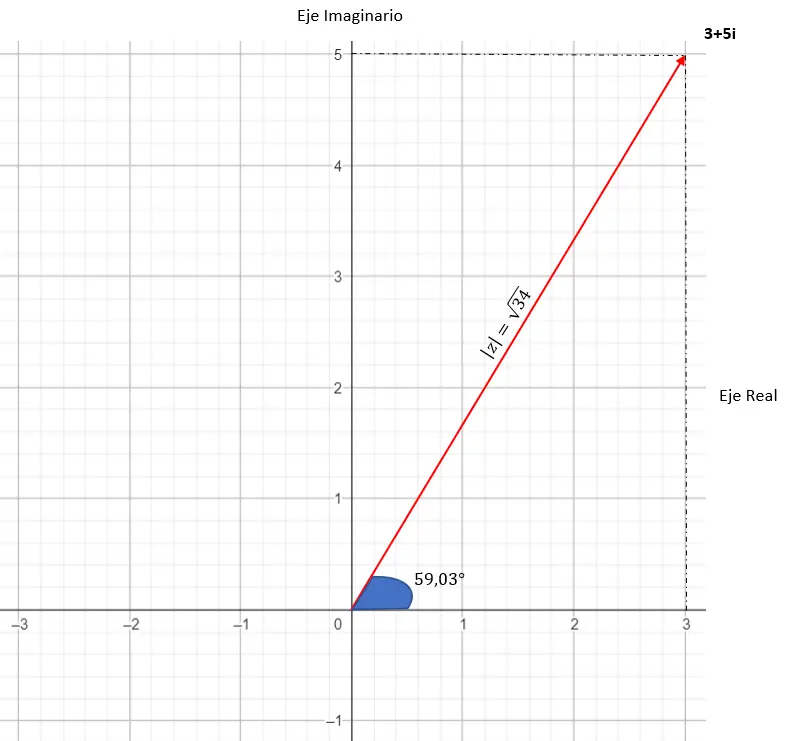
La sua rappresentazione grafica è la seguente:
3. Forma trigonometrica
Infine, abbiamo la notazione trigonometrica , che si calcola dalla formula di Eulero :

Ad esempio, per esprimere i numeri 4 – 3i in forma trigonometrica, seguiamo la seguente procedura:
Iniziamo calcolando il modulo e l’argomento con le formule che abbiamo usato nella sezione della forma polare.
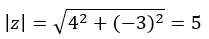
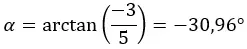
ATTENZIONE: L’argomento è nel quarto quadrante, perché (a > 0 e b < 0).
Aggiungiamo i dati nell’equazione in forma trigonometrica.
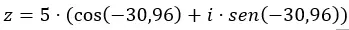
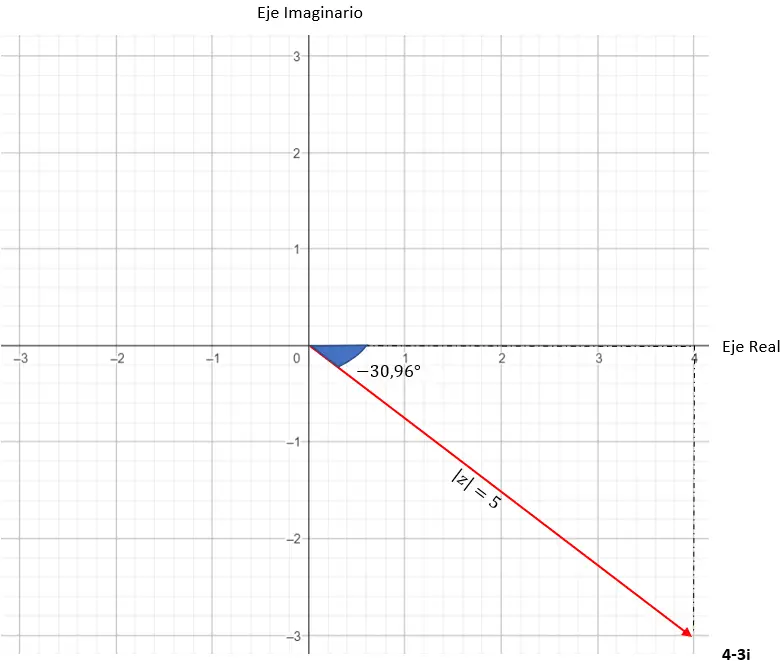
E abbiamo già il numero espresso in forma trigonometrica. La sua rappresentazione grafica è la seguente.
Come passare da una tipologia all’altra?
Ora conosci tutti i modi per esprimere un numero complesso. E nell’ultima sezione hai potuto vedere come accedere a ciascuno di essi, ma prima di concludere vogliamo fornire un breve riepilogo di come passare da un modulo all’altro. Solo tu devi utilizzare le formule che abbiamo visto nella sezione precedente.
Dalla forma binomiale a quella polare e viceversa
Per passare dal binomio al polare proponiamo il seguente diagramma:
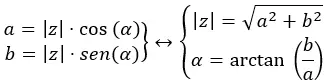
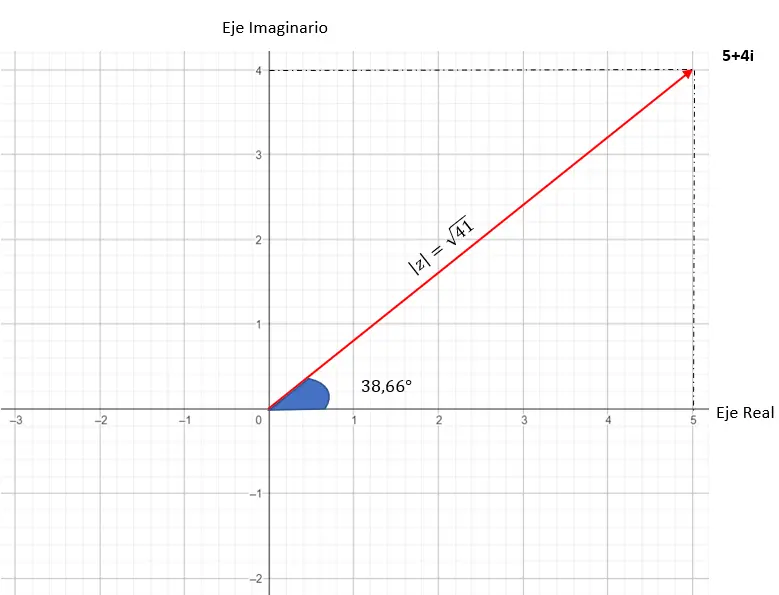
Abbiamo visto un esempio prima in cui siamo passati dal binomio al polare, quindi ora passeremo dal polare al binomio utilizzando il diagramma sopra. Dobbiamo convertire √41 38,66 in un binomio.
Per prima cosa calcoliamo l’a.
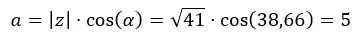
Quindi calcoliamo b.
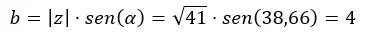
E lo esprimiamo in forma binomiale.
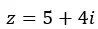
La rappresentazione grafica di questo numero è simile alla seguente:
Dalla forma binomiale alla forma trigonometrica e viceversa
Per passare dal binomio al trigonometrico bisogna applicare anche le formule di cui abbiamo parlato nella sezione precedente. In questo modo calcoliamo prima il modulo e l’argomento, quindi inseriamo questi dati nell’equazione della forma trigonometrica. Per fare un esempio, passeremo trigonometricamente il numero z = 3 + 2i .
Per prima cosa calcoliamo il modulo e l’argomento.
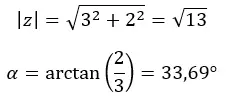
ATTENZIONE: L’argomento è nel primo quadrante, perché (a > 0 e b > 0).
Quindi, completiamo l’equazione in forma trigonometrica con questi dati.
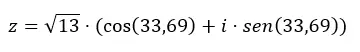
E se vogliamo passare dal trigonometrico al binomio non dobbiamo fare altro che risolvere l’espressione precedente.
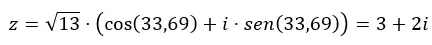
Dalla forma polare alla forma trigonometrica e viceversa
Infine passeremo dalla forma polare alla forma trigonometrica. Il che è abbastanza semplice, perché queste due forme sono espresse dagli stessi due valori: modulo e argomento . Quindi devi solo compilare i moduli e il gioco è fatto.
Facciamo un esempio, convertiremo il numero z = √85 12,53 in forma trigonometrica.
Riformuliamo le due variabili (modulo e argomento) nell’equazione della forma trigonometrica:
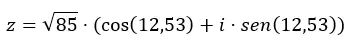
Quindi ora che sai come passare da una forma all’altra, ti consigliamo di esercitarti un po’ con alcuni esercizi . In questo modo consoliderai le conoscenze apprese in questo articolo. Se hai domande su questo argomento, sentiti libero di lasciarle nei commenti. E se vuoi saperne di più sui numeri complessi, controlla i link sottostanti.
Ulteriori informazioni sui numeri complessi
- numeri immaginari
- Proprietà dei numeri complessi
- Operazioni con numeri complessi
- radici di numeri complessi
- Rappresentazione grafica dei numeri complessi