▷ Tutto sulla geometria analitica nello spazio ✅

In questa pagina troverai la spiegazione di tutto ciò che riguarda la geometria analitica nello spazio (e le formule): le equazioni della retta e del piano, le posizioni relative tra piani e rette, come si calcolano le distanze e gli angoli nello spazio,…

Cos’è la geometria nello spazio?

La geometria spaziale è la branca della geometria responsabile dello studio delle figure geometriche tridimensionali (3D), cioè quelle che occupano un posto nello spazio. Come il cono, il cubo, la piramide, la sfera, il cilindro, i prismi, i poliedri, ecc.

Tuttavia in questa pagina ci concentreremo sulla geometria analitica nello spazio , quella parte della geometria spaziale che si concentra sull’analisi dei punti, delle linee, dei piani, delle distanze tra due figure geometriche, dell’angolo che formano, dei punti di intersezione tra diverse geometrie figure. elementi, ecc.

Equazioni della retta nello spazio

Ricordiamo che la definizione matematica di linea è un insieme di punti consecutivi rappresentati nella stessa direzione senza curve o angoli.

Quindi, per esprimere matematicamente qualsiasi linea in uno spazio tridimensionale (in R3) utilizziamo le equazioni della linea, e per trovarle abbiamo solo bisogno di un punto che appartiene alla linea e del vettore direzione di detta linea.

Solo con questi due elementi geometrici si possono trovare assolutamente tutte le diverse equazioni della retta, che sono le seguenti:

Le equazioni della retta sono l’ equazione vettoriale , le equazioni parametriche , l’ equazione continua e l’ equazione implicita (o generale) .

Di seguito hai una spiegazione dei diversi tipi di equazioni della linea.

Equazione vettoriale della retta nello spazio

Sì

$\vv{\text{v}}$

è il vettore direzione della linea e

$P$

un punto che appartiene a destra:

$\vv{\text{v}}= (\text{v}_x,\text{v}_y,\text{v}_z) \qquad P(P_x,P_y,P_z)$

La formula per l’equazione vettoriale della retta è:

$\definecolor{taronjaquadreejemplo}{HTML}{FF9800} \newtcbox{\mymath}[1][]{% nobeforeafter, math upper, tcbox raise base, enhanced, colframe=taronjaquadreejemplo, boxrule=1.1pt, boxsep=2mm, #1} \begin{empheq}[box={\mymath[colback=white, shadow={2mm}{-2mm}{0mm}{taronjaquadreejemplo!20!white,} ]}]{equation*} (x,y,z)=(P_x,P_y,P_z)+t\cdot (\text{v}_x,\text{v}_y,\text{v}_z) \end{empheq}$

Equazioni parametriche della retta nello spazio

Possiamo ottenere la formula per l’equazione parametrica di una linea dalla sua equazione vettoriale equiparando componente a componente:

$\definecolor{taronjaquadreejemplo}{HTML}{FF9800} \newtcbox{\mymath}[1][]{% nobeforeafter, math upper, tcbox raise base, enhanced, colframe=taronjaquadreejemplo, boxrule=1.1pt, boxsep=2mm, #1} \begin{empheq}[box={\mymath[colback=white, shadow={2mm}{-2mm}{0mm}{taronjaquadreejemplo!20!white,} ]}]{equation*} \displaystyle \begin{cases} x=P_x+t\cdot\text{v}_x \\[1.7ex] y=P_y+t\cdot\text{v}_y \\[1.7ex] z=P_z+t\cdot\text{v}_z\end{cases} \end{empheq}$

Equazione continua della retta nello spazio

La formula per l’ equazione continua della retta è:

$\definecolor{taronjaquadreejemplo}{HTML}{FF9800} \newtcbox{\mymath}[1][]{% nobeforeafter, math upper, tcbox raise base, enhanced, colframe=taronjaquadreejemplo, boxrule=1.1pt, boxsep=2mm, #1} \begin{empheq}[box={\mymath[colback=white, shadow={2mm}{-2mm}{0mm}{taronjaquadreejemplo!20!white,} ]}]{equation*} \cfrac{x-P_x}{\text{v}_x}=\cfrac{y-P_y}{\text{v}_y}= \cfrac{z-P_z}{\text{v}_z} \end{empheq}$

Questo tipo di equazione della retta può essere ottenuta anche da equazioni parametriche, puoi vedere la dimostrazione sulla nostra pagina dell’equazione continua , inoltre potrai anche vedere esempi ed esercitarti con esercizi di equazioni risolti da destra.

Equazioni generali (o implicite) della retta nello spazio

Infine, moltiplicando due per due le frazioni dell’equazione continua della retta, otteniamo le equazioni generali (o implicite) della retta :

$\definecolor{taronjaquadreejemplo}{HTML}{FF9800} \newtcbox{\mymath}[1][]{% nobeforeafter, math upper, tcbox raise base, enhanced, colframe=taronjaquadreejemplo, boxrule=1.1pt, boxsep=2mm, #1} \begin{empheq}[box={\mymath[colback=white, shadow={2mm}{-2mm}{0mm}{taronjaquadreejemplo!20!white,} ]}]{equation*} \displaystyle \begin{cases} A_1x+B_1y+C_1z+D_1=0 \\[1.7ex] A_2x+B_2y+C_2z+D_2=0\end{cases} \end{empheq}$

Questo tipo di equazione della retta è anche chiamata equazione cartesiana.

Abbiamo appena visto le 4 equazioni più rilevanti della retta (vettoriale, parametrica, continua e generale), esiste però un’altra equazione un po’ particolare e quindi ci vuole una pagina intera per spiegarla. Questa è l’ equazione canonica , in questo link potete vedere tutta la sua spiegazione, perché è così speciale e cosa la rende diversa da tutte le altre.

Equazioni piane nello spazio

Nella geometria analitica, l’ equazione di un piano è un’equazione che consente di esprimere analiticamente qualsiasi piano. Quindi per trovare l’equazione di un piano bastano un punto e due vettori linearmente indipendenti appartenenti a detto piano.

Pertanto, tutti i tipi di equazioni del piano sono: l’ equazione vettoriale , le equazioni parametriche , l’ equazione implicita (o generale) e l’ equazione canonica (o segmentale) del piano.

Successivamente vedremo la spiegazione e la formula di tutte le equazioni del piano.

Equazione vettoriale del piano

Dati un punto e due vettori direzionali di un piano:

$\begin{array}{c} P(P_x,P_y,P_z) \\[2ex] \vv{\text{u}}=(\text{u}_x,\text{u}_y,\text{u}_z)\\[2ex] \vv{\text{v}}=(\text{v}_x,\text{v}_y,\text{v}_z)\end{array}$

La formula per l’equazione vettoriale di un piano è:

$\definecolor{taronjaquadreejemplo}{HTML}{FF9800} \newtcbox{\mymath}[1][]{% nobeforeafter, math upper, tcbox raise base, enhanced, colframe=taronjaquadreejemplo, boxrule=1.1pt, boxsep=2mm, #1} \begin{empheq}[box={\mymath[colback=white, shadow={2mm}{-2mm}{0mm}{taronjaquadreejemplo!20!white,} ]}]{equation*} (x,y,z)=P+\lambda \vv{\text{u}} + \mu \vv{\text{v}} \end{empheq}$

O equivalente:

$(x,y,z)=(P_x,P_y,P_z)+\lambda (\text{u}_x,\text{u}_y,\text{u}_z) + \mu (\text{v}_x,\text{v}_y,\text{v}_z)$

Oro

$\lambda$

$\mu$

Sono due scalari, cioè due numeri reali.

Equazioni parametriche del piano

D’altra parte, la formula per l’ equazione parametrica del piano è:

$\definecolor{taronjaquadreejemplo}{HTML}{FF9800} \newtcbox{\mymath}[1][]{% nobeforeafter, math upper, tcbox raise base, enhanced, colframe=taronjaquadreejemplo, boxrule=1.1pt, boxsep=2mm, #1} \begin{empheq}[box={\mymath[colback=white, shadow={2mm}{-2mm}{0mm}{taronjaquadreejemplo!20!white,} ]}]{equation*} \displaystyle \begin{cases}x=P_x + \lambda \text{u}_x + \mu \text{v}_x \\[1.7ex] y=P_y + \lambda \text{u}_y + \mu \text{v}_y\\[1.7ex] z=P_z + \lambda\text{u}_z + \mu \text{v}_z \end{cases} \end{empheq}$

Equazione implicita o generale del piano

L’equazione implicita di un piano, detta anche equazione generale, si ottiene risolvendo il seguente determinante e ponendo il risultato a 0:

$\displaystyle \begin{vmatrix}\text{u}_x & \text{v}_x & x-P_x \\[1.1ex]\text{u}_y & \text{v}_y & y-P_y \\[1.1ex]\text{u}_z & \text{v}_z & z-P_z \end{vmatrix} = 0$

Pertanto l’ equazione implicita o generale del piano risultante sarà della forma seguente:

Questo tipo di equazione piana è anche chiamata equazione piana cartesiana.

Equazione canonica o segmentale del piano

La formula per l’equazione canonica o segmentale di un piano è la seguente:

$\definecolor{taronjaquadreejemplo}{HTML}{FF9800} \newtcbox{\mymath}[1][]{% nobeforeafter, math upper, tcbox raise base, enhanced, colframe=taronjaquadreejemplo, boxrule=1.1pt, boxsep=2mm, #1} \begin{empheq}[box={\mymath[colback=white, shadow={2mm}{-2mm}{0mm}{taronjaquadreejemplo!20!white,} ]}]{equation*} \displaystyle \cfrac{x}{a}+\cfrac{y}{b} + \cfrac{z}{c} = 1 \end{empheq}$

Oro:

$a$

Questo è il punto di intersezione tra il piano e l’asse X.
$b$

Questo è il punto di intersezione tra il piano e l’asse Y.
$c$

Qui è dove il piano interseca l’asse Z.

Vettore normale ad un piano

Il vettore normale ad un piano è un vettore perpendicolare a tutte le rette contenute in questo piano. Pertanto un vettore normale ad un piano significa che è perpendicolare al piano.

Molti problemi metrici nella geometria analitica spaziale riguardano i piani e i loro vettori normali. Per risolvere questi esercizi basta conoscere la relazione matematica tra un piano e il suo vettore normale:

Le componenti X, Y, Z del vettore normale ad un piano coincidono rispettivamente con i coefficienti A, B, C dell’equazione implicita (o generale) di detto piano.

$\displaystyle \color{orange} \boxed{ \color{black} \quad \pi : \ Ax+By+C+D = 0 \quad \iff \quad \vv{n} = (A,B,C) \quad \vphantom{\Bigl(}}$

Oro

$\vv{n}$

è il vettore ortogonale al piano

$\pi.$

Posizioni relative di due elementi geometrici nello spazio

Ovviamente una linea o un piano non devono necessariamente essere soli nello spazio, ma al contrario, normalmente interagiscono tra loro: si intersecano, sono paralleli, perpendicolari, ecc. Bene, in questa sezione vedremo le diverse posizioni relative di linee e piani e come vengono determinate.

Posizione relativa di due linee nello spazio

Nella geometria analitica, quando si lavora in uno spazio tridimensionale (in R3) ci sono 4 possibili posizioni relative tra due linee: due linee possono essere linee coincidenti , linee parallele , linee secanti o linee secanti .

Linee parallele

posizione relativa di due rette parallele

Due rette sono parallele se hanno la stessa direzione ma non hanno alcun punto in comune. Inoltre, le linee parallele sono sempre alla stessa distanza l’una dall’altra.

Linee coincidenti

Due rette coincidono se hanno la stessa direzione e se tutti i loro punti sono comuni.

Linee di intersezione

posizione relativa di due linee che si intersecano

Due linee che si intersecano hanno direzioni diverse ma si toccano in un punto.

Linee di intersezione

Due linee che si intersecano hanno direzioni diverse e non si intersecano in nessun punto. Due linee incrociate quindi non sono sullo stesso piano. Ad esempio, nella rappresentazione grafica sopra la linea

$s$

è sempre davanti alla retta

$r$

, quindi non si toccheranno mai.

Come trovare la posizione relativa di due linee in base agli intervalli

Un modo per trovare la posizione relativa di due righe è calcolare gli intervalli di due matrici specifiche, come vedremo di seguito. Questo metodo è molto utile quando le due linee sono espresse sotto forma di un’equazione implicita (o generale).

Quindi, se abbiamo due linee espresse con le loro equazioni implicite (o generali) in uno spazio tridimensionale (in R3):

$\displaystyle r: \ \begin{cases}A_1x+B_1y+C_1z+D_1=0 \\[2ex] A_2x+B_2y+C_2z+D_2=0 \end{cases}$

$\displaystyle s: \ \begin{cases}A_3x+B_3y+C_3z+D_3=0 \\[2ex] A_4x+B_4y+C_4z+D_4=0 \end{cases}$

Sia A la matrice composta dai coefficienti delle due rette:

$\displaystyle A=\begin{pmatrix}A_1 & B_1 & C_1\\[1.1ex]A_2 & B_2 & C_2\\[1.1ex]A_3 & B_3 & C_3\\[1.1ex]A_4 & B_4 & C_4 \end{pmatrix}$

E data la matrice espansa A’, che è la matrice formata da tutti i parametri delle due linee:

$\displaystyle A'=\begin{pmatrix}A_1 & B_1 & C_1&D_1\\[1.1ex]A_2 & B_2 & C_2&D_2\\[1.1ex]A_3 & B_3 & C_3&D_3\\[1.1ex]A_4 & B_4 & C_4&D_4 \end{pmatrix}$

Quindi, la posizione relativa delle due linee può essere determinata dall’estensione delle due matrici precedenti secondo la seguente tabella:

posizioni relative di due linee per intervalli

Pertanto, per trovare la posizione relativa tra due righe dovremo calcolare gli intervalli di entrambe le matrici e a seconda dell’intervallo di ciascuna matrice sarà l’uno o l’altro caso.

Questo teorema può essere dimostrato utilizzando il teorema di Rouché-Frobenius (un metodo utilizzato per risolvere sistemi di equazioni lineari), tuttavia in questa pagina non faremo la dimostrazione perché è piuttosto macchinosa e non aggiunge molto. .

Posizione relativa di due piani nello spazio

Nella geometria analitica, ci sono solo tre possibili posizioni relative tra due piani: piani intersecanti, piani paralleli e piani coincidenti.

Piani che si intersecano : due piani si intersecano se si intersecano solo su una linea.
Piani paralleli : due piani sono paralleli se non si intersecano in nessun punto.
Piani coincidenti : due piani sono coincidenti se hanno tutti i punti in comune.

Scatti incrociati

posizione relativa di due piani che si intersecano

piani paralleli

Piani di corrispondenza

posizione relativa di due piani coincidenti

Come determinare la posizione relativa di due piani mediante coefficienti

Un modo per conoscere la posizione relativa tra due piani è utilizzare i coefficienti delle loro equazioni generali (o implicite).

Consideriamo quindi l’equazione generale (o implicita) di due piani diversi:

$\pi_1 : \ Ax+By+Cz+D=0$

$\pi_2 : \ A'x+B'y+C'z+D'=0$

La posizione relativa tra i due piani in uno spazio tridimensionale dipende dalla proporzionalità dei loro coefficienti o parametri:

posizione relativa di due piani con parametri

Pertanto, i due piani si intersecheranno quando uno dei coefficienti A, B o C non è proporzionale agli altri. I due piani saranno invece paralleli quando solo i termini indipendenti non saranno proporzionali. E infine, i piani coincideranno quando tutti i coefficienti delle due equazioni saranno proporzionali.

Distanze nello spazio

Di seguito sono riportate le formule per calcolare la distanza tra diversi elementi geometrici: tra un punto e una linea, tra due piani, tra un piano e una linea,…

Distanza tra due punti

La distanza tra due punti corrisponde alla norma del vettore determinato da questi 2 punti.

Quindi se abbiamo due punti generici:

$A(a_x,a_y,a_z) \qquad \qquad B(b_x,b_y,b_z)$

La formula per la distanza tra i due punti è:

$\definecolor{taronjaquadreejemplo}{HTML}{FF9800} \newtcbox{\mymath}[1][]{% nobeforeafter, math upper, tcbox raise base, enhanced, colframe=taronjaquadreejemplo, boxrule=1.1pt, boxsep=2mm, #1} \begin{empheq}[box={\mymath[colback=white, shadow={2mm}{-2mm}{0mm}{taronjaquadreejemplo!20!white,} ]}]{equation*} \displaystyle d(A,B) = \vert \vv{AB} \rvert = \sqrt{(b_x-a_x)^2+(b_y-a_y)^2+(b_z-a_z)^2} \end{empheq}$

Distanza da un punto a una linea

La formula per calcolare la distanza da un punto a una linea nello spazio è:

$\definecolor{taronjaquadreejemplo}{HTML}{FF9800} \newtcbox{\mymath}[1][]{% nobeforeafter, math upper, tcbox raise base, enhanced, colframe=taronjaquadreejemplo, boxrule=1.1pt, boxsep=2mm, #1} \begin{empheq}[box={\mymath[colback=white, shadow={2mm}{-2mm}{0mm}{taronjaquadreejemplo!20!white,} ]}]{equation*} \displaystyle d(s,r)=d(P,r)=\cfrac{\lvert \vv{QP} \times \vv{\text{v}}_r \rvert}{\lvert \vv{\text{v}}_r \rvert} \end{empheq}$

Oro:

$\lvert \vv{\text{v}}_r \rvert$

è il modulo del vettore direzione della linea

$r.$
$Q$

è un punto a destra

$r,$

$P$

un punto sulla linea

$s$

E

$\vv{QP}$

il vettore definito dai due punti
$\lvert \vv{QP} \times \vv{\text{v}}_r \rvert$

è il modulo del prodotto vettoriale tra i vettori

$\vv{QP}$

E

$\vv{\text{v}}_r$

Distanza tra due linee

La distanza tra due linee dipende dalla loro posizione relativa:

Se le due linee coincidono o si intersecano , la distanza tra le due linee è pari a zero, poiché si intersecano (almeno) in un punto.
Quando le due rette sono parallele o si intersecano è necessario applicare una formula a seconda dei casi (entrambe le spiegazioni sono disponibili di seguito).

Distanza tra due rette parallele

Due rette parallele sono sempre alla stessa distanza. Quindi per calcolare la distanza tra due linee parallele nello spazio (in R3) si fa nello stesso modo che nel piano (in R2): basta prendere un punto su una delle due linee e trovare la distanza lì Questo va da questo punto all’altra linea.

Quindi per determinare la distanza tra 2 linee parallele è necessario utilizzare la formula per la distanza tra un punto e una linea.

Distanza tra due linee che si intersecano

Sia il vettore direzione e qualsiasi punto di due linee che si intersecano:

$\displaystyle r: \ \begin{cases} \vv{\text{u}} \\[2ex] A\end{cases} \qquad \qquad s: \ \begin{cases} \vv{\text{v}} \\[2ex] B\end{cases}$

La formula per la distanza tra due linee che si intersecano è:

$\definecolor{taronjaquadreejemplo}{HTML}{FF9800} \newtcbox{\mymath}[1][]{% nobeforeafter, math upper, tcbox raise base, enhanced, colframe=taronjaquadreejemplo, boxrule=1.1pt, boxsep=2mm, #1} \begin{empheq}[box={\mymath[colback=white, shadow={2mm}{-2mm}{0mm}{taronjaquadreejemplo!20!white,} ]}]{equation*} \displaystyle d(r,s)=\cfrac{\left|\left[\vv{\text{u}},\vv{\text{v}},\vv{AB}\right]\right|}{\lvert \vv{\text{u}} \times \vv{\text{v}} \rvert} \end{empheq}$

Oro:

$\left|\left[\vv{\text{u}},\vv{\text{v}},\vv{AB}\right]\right|$

è il valore assoluto del prodotto misto dei vettori

$\vv{\text{u}}, \vv{\text{v}}$

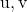
e il vettore definito dai punti

$A$

E

$B$

.
$\lvert \vv{\text{u}} \times \vv{\text{v}} \rvert$

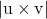
è il modulo del prodotto vettoriale tra i vettori di direzione delle due linee incrociate.

Anche se qui hai la formula, determinare la distanza tra due linee che si intersecano è più complicato di quanto sembri. Quindi se vuoi esercitarti nel link seguente puoi vedere esempi ed esercizi risolti sulla distanza tra due linee che si intersecano.

Distanza da un punto a un piano

Dato un punto e l’equazione generale (o implicita) di un piano:

$P(x_0,y_0,z_0) \qquad \qquad \pi: \ Ax+By+Cz+D=0$

La formula per la distanza da un punto a un piano è:

$\definecolor{taronjaquadreejemplo}{HTML}{FF9800} \newtcbox{\mymath}[1][]{% nobeforeafter, math upper, tcbox raise base, enhanced, colframe=taronjaquadreejemplo, boxrule=1.1pt, boxsep=2mm, #1} \begin{empheq}[box={\mymath[colback=white, shadow={2mm}{-2mm}{0mm}{taronjaquadreejemplo!20!white,} ]}]{equation*} \displaystyle d(P,\pi) = \cfrac{\lvert A\cdot x_0+B\cdot y_0+C\cdot z_0+D\rvert}{\sqrt{A^2+B^2+C^2}} \end{empheq}$

qual è la distanza da un punto a un piano

Se applicando la formula otteniamo un risultato pari a zero, ciò significa ovviamente che la distanza tra il punto e il piano è zero e, quindi, il punto fa parte di questo piano.

Distanza tra due piani

La distanza tra due piani nello spazio dipende dalla posizione relativa tra questi due piani:

Se i due piani si intersecano o coincidono , la distanza tra loro è pari a zero perché si intersecano in un certo punto.
Se i due piani sono paralleli , la distanza tra i due piani si calcola prendendo un punto su uno dei due piani e calcolando la distanza tra quel punto e l’altro piano.

Distanza tra due piani paralleli

Due piani paralleli sono sempre alla stessa distanza l’uno dall’altro, quindi per trovare la distanza tra due piani paralleli possiamo prendere un punto su uno dei due piani e calcolare la distanza da quel punto all’altro piano.

Quindi per calcolare la distanza tra due piani paralleli è necessario trovare un punto su uno dei due piani quindi utilizzare la formula per la distanza tra un punto e un piano.

Angoli nello spazio

Come per le distanze, la determinazione dell’angolo tra due oggetti geometrici nello spazio dipende dalle loro caratteristiche geometriche. Perché calcolare l’angolo formato da due rette non è la stessa cosa che calcolare l’angolo formato da due piani. Quindi di seguito hai le formule per trovare gli angoli tra linee e piani.

Angolo tra due linee

Per conoscere l’angolo tra due rette nello spazio euclideo dobbiamo calcolare l’angolo formato dai loro vettori di direzione, quindi:

Dati i vettori direzione di due linee diverse:

$\vv{\text{u}} = (\text{u}_x,\text{u}_y,\text{u}_z)\qquad \vv{\text{v}} = (\text{v}_x,\text{v}_y,\text{v}_z)$

L’ angolo formato da queste due linee può essere calcolato con la seguente formula:

$\definecolor{taronjaquadreejemplo}{HTML}{FF9800} \newtcbox{\mymath}[1][]{% nobeforeafter, math upper, tcbox raise base, enhanced, colframe=taronjaquadreejemplo, boxrule=1.1pt, boxsep=2mm, #1} \begin{empheq}[box={\mymath[colback=white, shadow={2mm}{-2mm}{0mm}{taronjaquadreejemplo!20!white,} ]}]{equation*} \displaystyle \cos(\alpha) =\cfrac{\lvert \vv{\text{u}} \cdot \vv{\text{v}}\rvert}{\lvert \vv{\text{u}} \rvert \cdot \lvert \vv{\text{v}} \rvert} \end{empheq}$

Oro

$\lvert \vv{\text{u}} \rvert$

$\lvert \vv{\text{v}} \rvert$

sono i moduli dei vettori

$\vv{\text{u}}$

$\vv{\text{v}}$

rispettivamente.

Ricordiamo che la formula per il modulo di un vettore è:

$\displaystyle \lvert \vv{\text{v}} \rvert = \sqrt{ \text{v}_x^2+\text{v}_y^2+\text{v}_z^2}$

Angolo tra due piani

L’angolo tra due piani è uguale all’angolo formato dai vettori normali di detti piani. Pertanto, per trovare l’angolo tra due piani, calcoliamo l’angolo formato dai loro vettori normali, poiché sono equivalenti .

Data l’equazione generale (o implicita) di due piani diversi:

$\pi_1 : \ A_1x+B_1y+C_1z+D_1=0$

$\pi_2 : \ A_2x+B_2y+C_2z+D_2=0$

Il vettore normale di ciascun piano è:

$\vv{n}_1=(A_1,B_1,C_1)$

$\vv{n}_2=(A_2,B_2,C_2)$

E l’angolo formato da questi due piani si determina calcolando l’angolo formato dai loro vettori normali utilizzando la seguente formula:

$\definecolor{taronjaquadreejemplo}{HTML}{FF9800} \newtcbox{\mymath}[1][]{% nobeforeafter, math upper, tcbox raise base, enhanced, colframe=taronjaquadreejemplo, boxrule=1.1pt, boxsep=2mm, #1} \begin{empheq}[box={\mymath[colback=white, shadow={2mm}{-2mm}{0mm}{taronjaquadreejemplo!20!white,} ]}]{equation*} \displaystyle \cos(\alpha) =\cfrac{\lvert \vv{n}_1 \cdot \vv{n}_2\rvert}{\lvert \vv{n}_1 \rvert \cdot \lvert \vv{n}_2 \rvert} \end{empheq}$

Angolo tra una linea e un piano

L’angolo formato da una linea e da un piano è definito come il minore dei due angoli complementari formati dal vettore direzione della linea e dal vettore normale del piano.

Pertanto, se

$\vv{\text{v}}$

è il vettore direzione della linea e

$\vv{n}$

è il vettore normale al piano:

$\vv{\text{v}} = (\text{v}_x,\text{v}_y,\text{v}_z)$

$\vv{n}=(n_x,n_y,n_z)$

La formula utilizzata per calcolare l’angolo formato da una linea e un piano è:

$\definecolor{taronjaquadreejemplo}{HTML}{FF9800} \newtcbox{\mymath}[1][]{% nobeforeafter, math upper, tcbox raise base, enhanced, colframe=taronjaquadreejemplo, boxrule=1.1pt, boxsep=2mm, #1} \begin{empheq}[box={\mymath[colback=white, shadow={2mm}{-2mm}{0mm}{taronjaquadreejemplo!20!white,} ]}]{equation*} \displaystyle \text{sen}(\alpha)=\cfrac{\lvert \vv{\text{v}} \cdot \vv{n}\rvert}{\lvert \vv{\text{v}} \rvert \cdot \lvert \vv{n} \rvert} \end{empheq}$

Geometria analitica nello spazio (formule)

Cos’è la geometria nello spazio?

Equazioni della retta nello spazio

Equazione vettoriale della retta nello spazio

Equazioni parametriche della retta nello spazio

Equazione continua della retta nello spazio

Equazioni generali (o implicite) della retta nello spazio

Equazioni piane nello spazio

Equazione vettoriale del piano

Equazioni parametriche del piano

Equazione implicita o generale del piano

Equazione canonica o segmentale del piano

Vettore normale ad un piano

Posizioni relative di due elementi geometrici nello spazio

Posizione relativa di due linee nello spazio

Come trovare la posizione relativa di due linee in base agli intervalli

Posizione relativa di due piani nello spazio

Come determinare la posizione relativa di due piani mediante coefficienti

Distanze nello spazio

Distanza tra due punti

Distanza da un punto a una linea

Distanza tra due linee

Distanza tra due rette parallele

Distanza tra due linee che si intersecano

Distanza da un punto a un piano

Distanza tra due piani

Distanza tra due piani paralleli

Angoli nello spazio

Angolo tra due linee

Angolo tra due piani

Angolo tra una linea e un piano

Lascia un commento Annulla risposta