La formula di Eulero è un concetto matematico che collega due concetti elementari della matematica: numeri complessi e trigonometria. Ciò la rende una delle concettualizzazioni più importanti e con il maggior numero di applicazioni in tutta la matematica. In questo articolo vedremo come si presenta questa formula e tutti gli usi che ha.
Qual è la formula di Eulero?
La formula di Eulero è un’equazione matematica fondamentale basata sul numero di Eulero , che mette in relazione i numeri complessi con la trigonometria. Fu scoperto dal matematico svizzero Leonhard Euler nel XVIII secolo e da allora è stato utilizzato in diversi campi, dalla fisica all’informatica.
La formula di Eulero è scritta come e ix = cos(x) + i sin(x) , dove e è la base del logaritmo naturale, i è l’ unità immaginaria (definita come radice quadrata di -1) e x è un valore reale numero. Questa equazione specifica che il numero complesso e ix è uguale alla somma del numero reale cos(x) e del prodotto del numero immaginario i per il numero reale sin(x).

L’importanza della formula di Eulero risiede nel fatto che consente di esprimere i numeri complessi in termini di numeri reali e trigonometria, rendendoli più facili da manipolare e calcolare.
Dimostrazione della formula di Eulero
La dimostrazione della formula di Eulero si basa sull’uso della serie di Taylor per la funzione esponenziale e dell’identità trigonometrica per coseno e seno.
Innanzitutto consideriamo la serie di Taylor per la funzione esponenziale:

Successivamente, sostituiamo x con ix nell’equazione precedente, dove i è l’unità immaginaria (radice quadrata di -1):
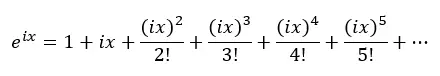
Quindi applichiamo le potenze di i e sostituiamo nell’equazione precedente:
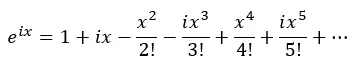
Ora raggruppiamo i termini reali e i termini con i:
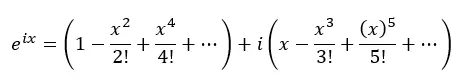
Infatti, ciascuna delle parentesi sopra è la serie di Taylor per coseno e seno:
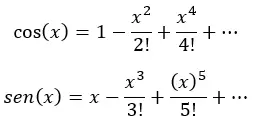
Infine semplifichiamo (sostituendo ogni espressione tra parentesi con coseno e seno di x) e otteniamo:

Esempio della formula di Eulero
Ora che sai come funziona questa formula matematica, ti consigliamo di provare a risolvere il seguente esempio pratico: Esprimere il numero complesso e 2i (in radianti) in forma binomiale:
L’applicazione principale della formula di Eulero è convertire un numero complesso espresso in forma esponenziale in forma binomiale. Utilizzeremo quindi la formula : e ix = cos(x) + i sin(x)
e 2i = cos(2) + i sin(2)
e2i = -0,416 + 0,909i
E avremmo già il numero in forma binomiale. Da lì possiamo realizzare la rappresentazione grafica nel piano complesso . Per fare ciò è necessario comprendere che un numero complesso si rappresenta nel piano complesso utilizzando come coordinate la parte reale sull’ascissa (asse x) e la parte immaginaria sull’ordinata (asse y).
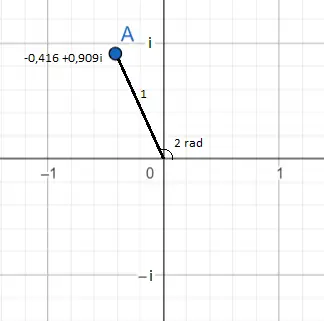
Nell’immagine precedente è mostrato il numero complesso e 2i , che è uguale a -0,416 + 0,909i. Questo può essere visto come un punto di colore blu. La sua posizione sull’aereo può essere vista da due angolazioni .
Il primo e più evidente è con la rappresentazione del numero in forma binomiale : -0,416 (sull’ascissa) e 0,909 (sul computer). E il secondo è in forma esponenziale : il modulo di e 2i è uguale a 1, perché è il numero che sta davanti ad e (poiché non c’è nessun numero davanti ad e, dobbiamo immaginare che ci sia un 1) e nell’esponente c’è 2, quindi l’argomento o l’angolo equivale a due radianti.
Se non capisci bene quest’ultimo paragrafo , ti consigliamo di leggere il nostro articolo sui numeri complessi. Bene, ecco una spiegazione molto approfondita dei diversi modi di scrivere un numero complesso e di tutte le sue proprietà.
Rappresentazione grafica della formula di Eulero
Nell’esempio precedente hai potuto vedere come viene applicata la formula di Eulero e come viene rappresentata graficamente nel piano complesso. Ma, se andiamo un po’ oltre e proviamo a rappresentare una funzione equivalente alla formula di Eulero, troviamo qualcosa di molto curioso: genera un cerchio di raggio 1 :
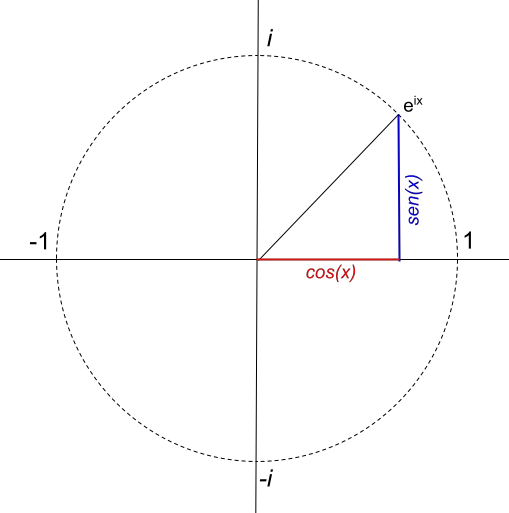
Tuttavia, il raggio del cerchio dipende direttamente dal valore del modulo del numero complesso. Se ad esempio vogliamo rappresentare un cerchio di raggio 4, la funzione sarà 4e ix . Quindi, la funzione 4e ix , è rappresentata così:
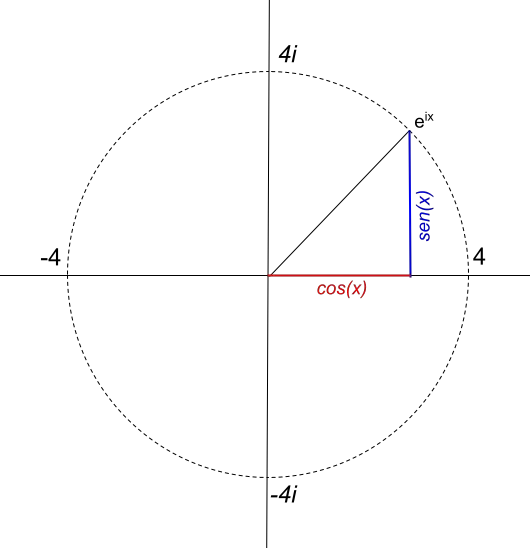
Ritornando alla circonferenza di raggio 1, se decidiamo di rappresentare e iπ (in radianti), dobbiamo prima calcolare:
eπi = cos(π) + i sin(π)
eπi = -1 + i0
eπi = -1
Otteniamo eπi = -1, che è la famosa identità di Eulero.
Da ciò deduciamo che il numero complesso e πi ha una sola parte reale, che è uguale a -1. Pertanto, la sua rappresentazione sarebbe tale che:
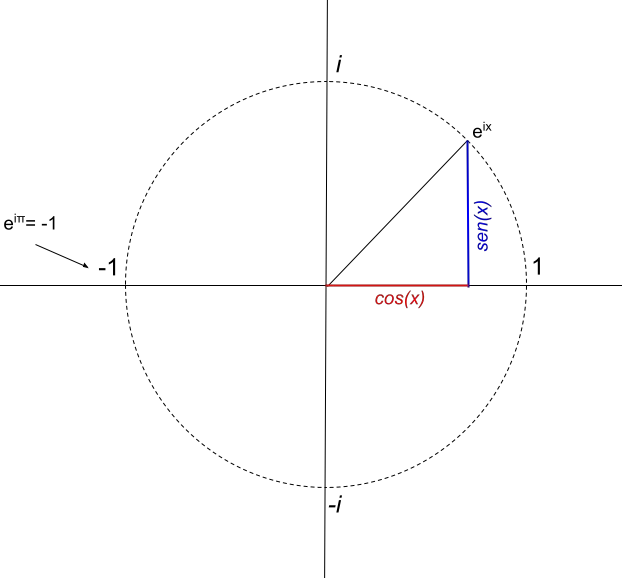
Applicazioni della formula di Eulero
- Numeri complessi: la formula di Eulero è una relazione tra funzioni trigonometriche e numeri complessi. Da questa formula possiamo esprimere i numeri complessi in diversi modi: binomiale, esponenziale e polare.
- Serie di Taylor: la formula di Eulero viene utilizzata per estendere le funzioni della serie di Taylor.
- Algebra lineare: la formula di Eulero viene utilizzata nella diagonalizzazione delle matrici, che è una tecnica fondamentale nell’algebra lineare.
- Calcolo differenziale e integrale: la formula di Eulero viene utilizzata nella soluzione di equazioni differenziali, che è una tecnica rilevante nel calcolo.
Inoltre, ha applicazioni in molte teorie matematiche e persino in concetti al di fuori del dominio matematico, come i teoremi di fisica.
conclusioni
Come hai visto in questo articolo, la massima applicazione della formula di Eulero è nei numeri complessi : nella sua espressione numerica e nella sua rappresentazione. È vero che questo ha qualche applicazione in algebra, ma essenzialmente stai lavorando con numeri complessi. È quindi importante soprattutto capirli bene.
Detto questo, speriamo di averti aiutato a comprendere meglio questo concetto. E se hai domande o non sai come svolgere un esercizio, non esitare a scriverci nei commenti.