Fonction de proportionnalité directe

Dans cet article, nous expliquons ce que sont les fonctions de proportionnalité directe, quelle est leur formule, comment les représenter dans un graphique et comment calculer leur équation à partir d’un point donné.

Qu’est-ce qu’une fonction de proportionnalité directe ?

La fonction de proportionnalité directe est également appelée fonction linéaire.

Rappelez-vous que deux grandeurs sont directement proportionnelles si l’une des grandeurs augmente de valeur alors que l’autre grandeur augmente également, et vice versa.

Formule de la fonction de proportionnalité directe

La formule qui définit la fonction de proportionnalité directe est la suivante :

où y est la variable indépendante, x est la variable dépendante et ym est la pente ou la constante de proportionnalité de la fonction.

Comme vous pouvez le voir, avec cette formule, il est très facile de calculer des valeurs de la magnitude y, il suffit de multiplier la valeur de la magnitude x par la pente de la fonction, caractéristique de chaque fonction de proportionnalité directe.

Par exemple, si nous avons la fonction de proportionnalité directe suivante :

Si nous voulons déterminer combien vaut la grandeur y lorsque x vaut 5, nous n’avons qu’à multiplier la pente de la fonction (3) par 5 :

Représentation graphique d’une fonction de proportionnalité directe

Ensuite, nous allons voir comment représenter graphiquement les fonctions de proportionnalité directe. Nous allons faire l’exercice suivant à titre d’exemple :

Pour représenter la fonction de proportionnalité directe sur un graphique, il suffit de tracer une droite passant par l’ origine des coordonnées (point (0,0)) et ayant la pente de la fonction.

Dans ce cas, la fonction que nous voulons représenter a une pente de

Par conséquent, la ligne doit croître de deux unités de y pour chaque unité de x.

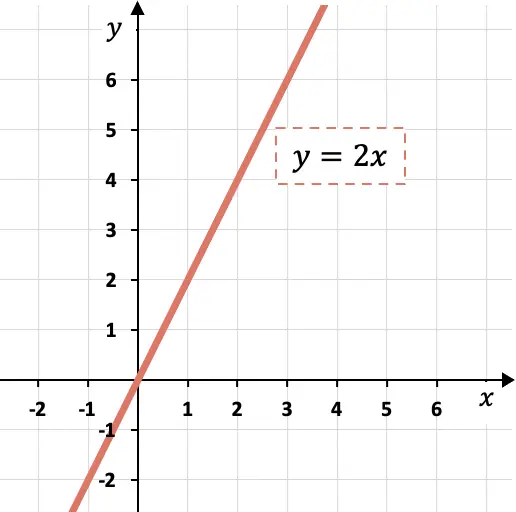
Comme vous pouvez le voir sur le graphique, si la pente est égale à 2, cela signifie que la magnitude y augmente deux fois plus que la magnitude x.

Les fonctions de proportionnalité directe ont un graphique très similaire aux fonctions affines, mais ce sont deux types de fonctions différents. Vous pouvez voir quelles sont les différences entre une fonction affine et une fonction linéaire dans le lien suivant :

➤ Voir : différence entre fonction linéaire et affine

Comment trouver la fonction de proportionnalité directe

Si nous connaissons un point de la fonction de proportionnalité directe, nous pouvons facilement trouver son équation. Voyons comment cela se fait en résolvant un problème de fonctions de proportionnalité directe :

• Le nombre de pièces qu’un peintre peint est approximativement directement proportionnel aux heures qu’il travaille, c’est-à-dire que plus il travaille d’heures, plus il peut peindre de pièces. Si nous savons qu’en une journée de 8 heures il a peint deux pièces entières, quelle est la fonction de proportionnalité directe qui relie le nombre de pièces peintes aux heures travaillées ?

Premièrement, nous devons déterminer quelle est la variable dépendante et quelle est l’indépendante. Le nombre de pièces peintes dépend des heures travaillées et non l’inverse. Par conséquent, la variable indépendante (x) est le nombre d’heures travaillées et la variable dépendante (y) est le nombre de pièces peintes.

Le problème nous dit que le peintre peut peindre 2 pièces en 8 heures, donc le graphe de la fonction doit passer par le point (8,2).

De plus, l’énoncé indique que les deux grandeurs ont une relation proportionnelle directe, ce qui signifie qu’elles sont mathématiquement liées à la formule de la fonction de proportionnalité directe :

Nous pouvons maintenant calculer la valeur de la pente de la fonction en substituant les coordonnées du point (8,2) dans l’équation :

Et, enfin, on résout l’inconnue m de l’équation :

En bref, la fonction de proportionnalité directe du problème est :

Tu pourrais aussi aimer:

• Fonction de proportionnalité inverse
• fonction constante