Fonction de proportionnalité inverse

Cette page explique ce que sont les fonctions de proportionnalité inverse et comment les représenter graphiquement. De plus, vous trouverez toutes les caractéristiques de ce type de fonction, comment calculer son domaine et aussi plusieurs exemples et exercices résolus pas à pas pour vous entraîner.

Qu’est-ce qu’une fonction de proportionnalité inverse ?

Ainsi, les fonctions de proportionnalité inverse sont toujours composées de fractions avec un polynôme du premier degré au dénominateur. Par conséquent, ils sont un type de fonction rationnelle.

Exemples de fonctions de proportionnalité inverse :

Généralement

est généralement la variable indépendante et la variable dépendante, ou en d’autres termes, la variable dépend de

D’autre part, le rapport de proportionnalité (le terme numérateur) peut être positif ou négatif et son signe marque l’augmentation ou la diminution de la fonction :

• Si la constante est négatif, la fonction est croissante.
• Au lieu de cela, si la constante est positif, la fonction est décroissante.

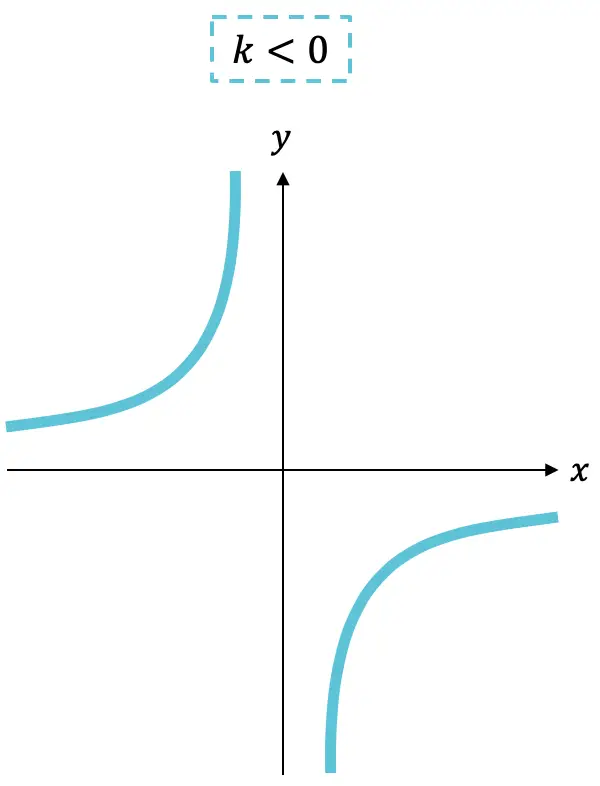
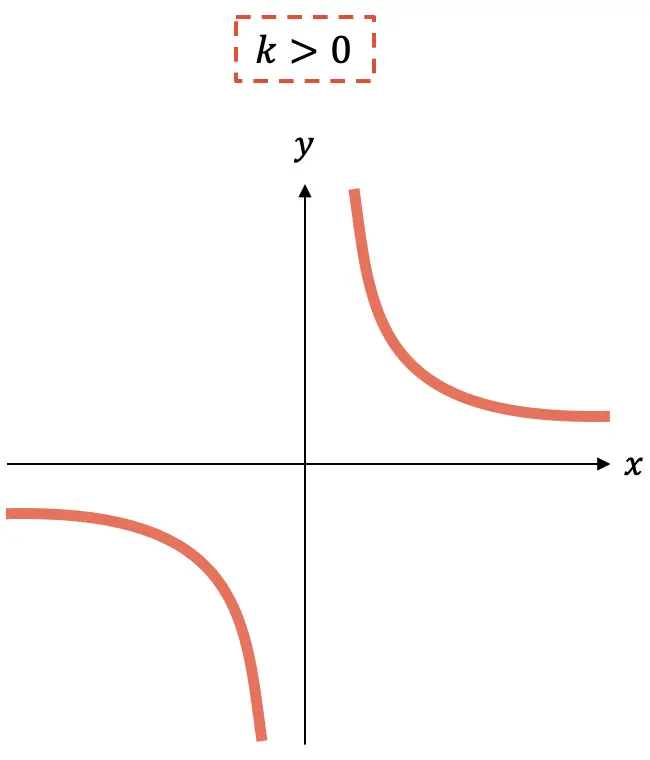
Comme vous pouvez le voir, le graphique d’une fonction de proportionnalité inverse est toujours composé de deux hyperboles qui, selon le signe de k , seront dans un quadrant ou un autre.

Domaine d’une fonction de proportionnalité inverse

Étant un type de fonction rationnelle, le domaine d’une fonction de proportionnalité inverse est tous les nombres réels sauf ceux qui disparaissent du dénominateur . Parce que le dénominateur ne peut jamais être nul car cela donnerait l’infini comme résultat.

A titre d’exemple, nous allons déterminer le domaine de la fonction de proportionnalité inverse suivante :

Pour savoir quand le dénominateur est nul, il faut égaliser son expression à 0 et résoudre l’équation :

Ainsi, lorsque x prend la valeur de 1, le dénominateur sera nul et on obtiendra une indétermination. Donc le domaine de la fonction est tous les nombres réels moins

Comment représenter graphiquement une fonction de proportionnalité inverse

Nous allons voir comment représenter graphiquement une fonction de proportionnalité inverse au moyen d’un exemple.

• Nous allons représenter la fonction suivante dans un graphe :

La première chose que nous devons faire est de trouver le domaine de la fonction. Étant une fraction, le dénominateur ne peut jamais être 0, car cela donnerait alors l’infini. Par conséquent, le domaine sera tout x sauf lorsque le dénominateur est annulé.

On fixe donc le dénominateur égal à 0 pour voir quel x n’appartient pas au domaine :

Par conséquent, le domaine de la fonction est tous les nombres sauf 2 :

Une fois que nous savons quel nombre n’appartient pas au domaine, nous créons une table de valeurs. Pour représenter des fonctions de proportionnalité inverse, il faut calculer 3 ou 4 points à gauche et 3 ou 4 points à droite du nombre qui n’appartient pas au domaine (2) :

Représentons maintenant les points sur un graphique :

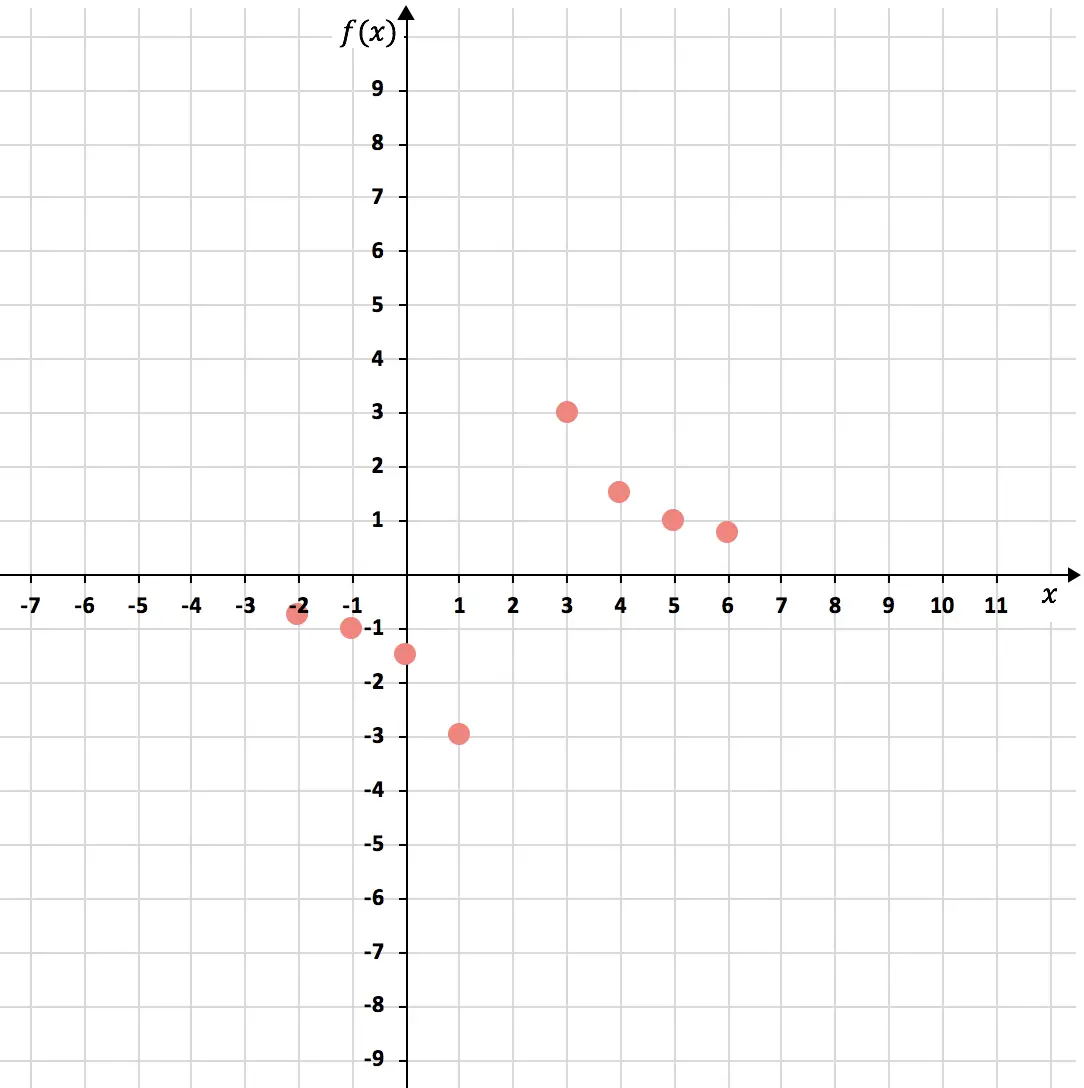
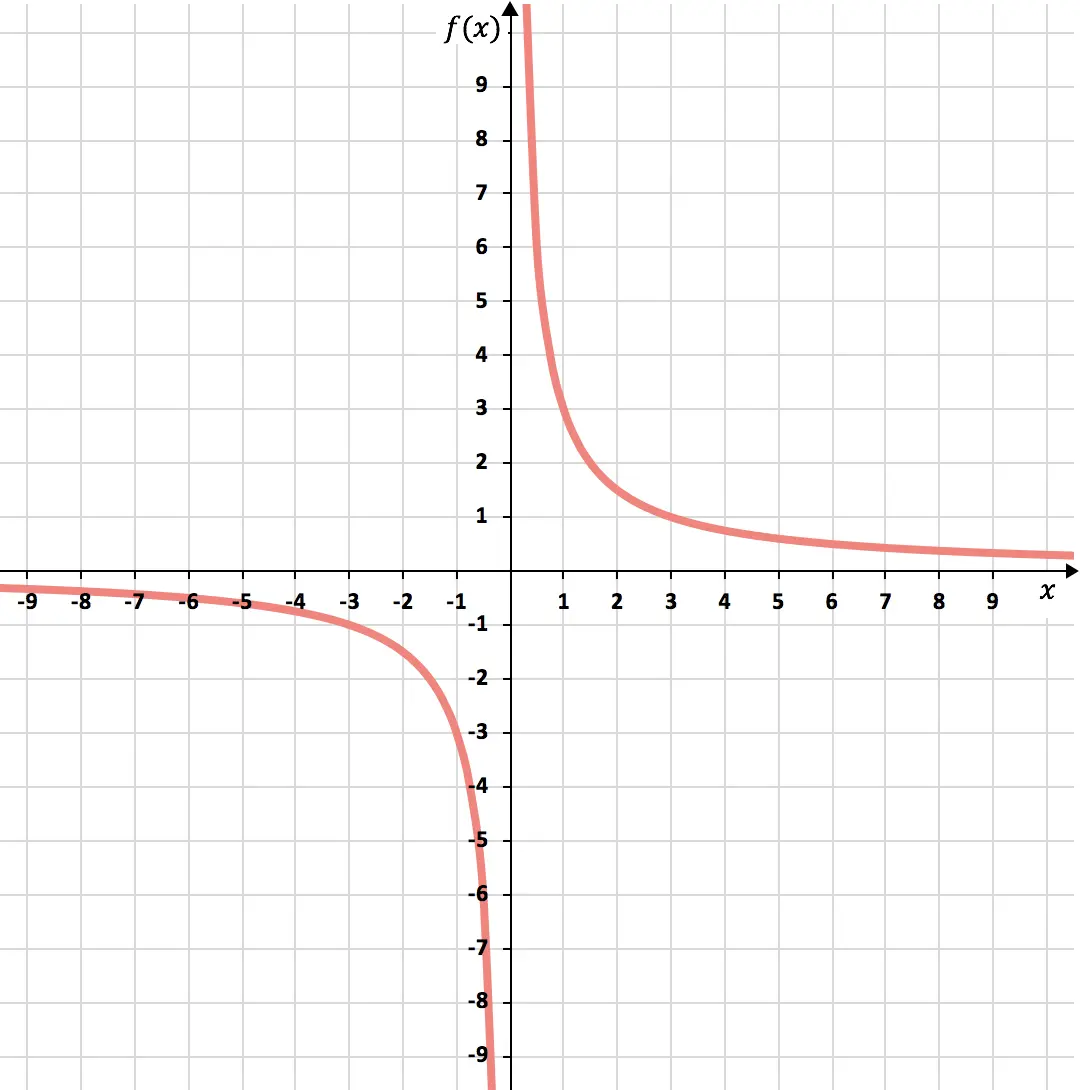
Et enfin nous joignons les points, formant les deux hyperboles de la fonction de proportionnalité inverse. De plus, nous allongeons les branches des hyperboles pour indiquer qu’elles continuent à croître :

Notez que la fonction se rapproche de

, tant à droite qu’à gauche. Cependant, il ne touche jamais tout à fait le 2, il s’en approche de très près mais ne le touche jamais. Donc, c’est une asymptote verticale . C’est parce que n’appartient pas au domaine de la fonction et, par conséquent, la fonction n’existe pas à ce point.

Et la même chose se produit avec l’axe horizontal X. La fonction se rapproche de

mais n’y touche jamais. Pourtant, est une asymptote horizontale .

Cela signifie que toutes les fonctions de proportionnalité inverse sont discontinues, car elles ont toujours une asymptote.

Vous pouvez en savoir plus sur les asymptotes et les limites des fonctions sur notre site Web.

Problèmes résolus des fonctions de proportionnalité inverse

Exercice 1

Calculez le domaine de la fonction de proportionnalité inverse suivante :

Une fonction de proportionnalité inverse n’existera pas lorsque le dénominateur est 0, car alors la fonction donnerait ∞. Par conséquent, nous devons fixer le dénominateur de la fonction égal à 0 pour voir que x annule le dénominateur et, par conséquent, n’appartient pas au domaine.

Exercice 2

Représentez graphiquement la fonction de proportionnalité inverse suivante :

La première chose à faire est de calculer le domaine de la fonction :

Une fois que nous savons quel nombre n’appartient pas au domaine, nous créons un tableau de valeurs avec la fonction :

Enfin, nous représentons les points obtenus sur le graphique et traçons les hyperboles, formant ainsi la fonction de proportionnalité inverse :

Exercice 3

Représentez graphiquement la fonction de proportionnalité inverse suivante :

La première chose à faire est de calculer le domaine de la fonction :

Une fois que nous connaissons le domaine de la fonction, nous construisons une table de valeurs :

Enfin, nous représentons les points obtenus sur un graphique et traçons les hyperboles, formant ainsi la fonction de proportionnalité inverse :

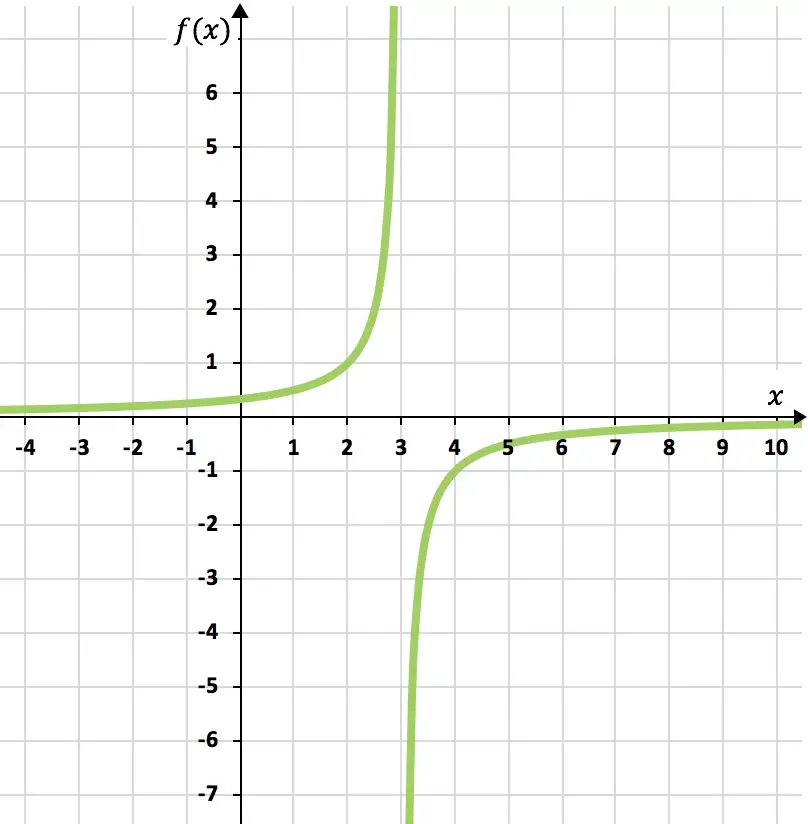
Exercice 4

Faites la représentation graphique de la fonction de proportionnalité inverse suivante :

Tout d’abord, nous devons calculer le domaine de la fonction :

Une fois que nous connaissons le domaine de la fonction, nous créons un tableau de valeurs :

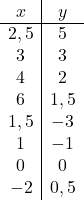
Et, enfin, on représente les points obtenus sur un graphique et on trace les hyperboles, formant ainsi la fonction de proportionnalité inverse :

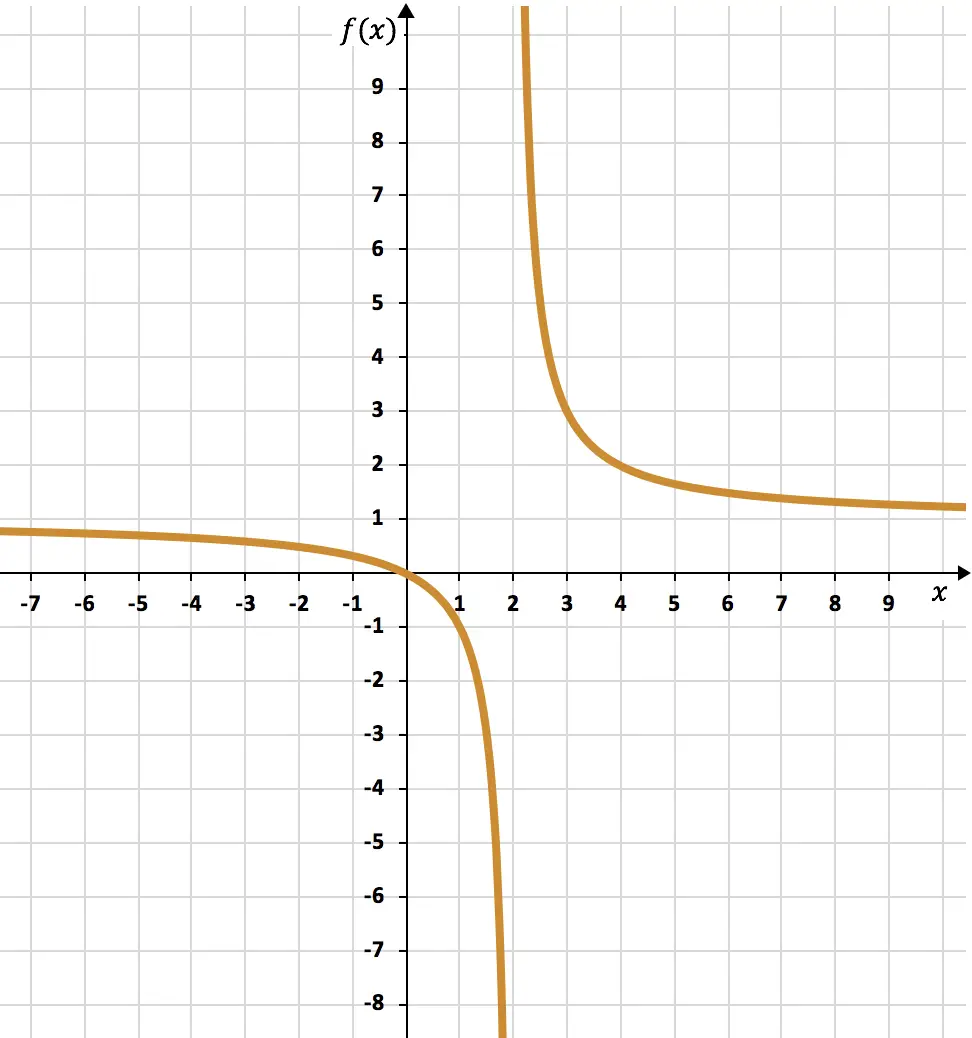
Exercice 5

Représentez graphiquement la fonction rationnelle suivante :

La première chose à faire est de calculer le domaine de la fonction :

Une fois que nous connaissons le domaine de la fonction, nous construisons une table de valeurs :

Pour finir, il suffit de représenter les points obtenus sur un graphique et de tracer les hyperboles, formant ainsi la fonction fractionnaire :

Applications de la fonction de proportionnalité inverse

La fonction de proportionnalité inverse apparaît dans de nombreux cas en physique et en mathématiques.

Par exemple, il est utilisé pour décrire la relation entre la pression et le volume dans un gaz parfait soumis à une température constante k. Cette fonction est appelée loi de Boyle-Mariotte (P×V=k) et est un exemple de fonction de proportionnalité inverse. Évidemment, le domaine de définition de cette fonction est limité uniquement à la branche positive, puisqu’il n’y a pas de volumes ou de pressions négatives.

La relation entre l’intensité du courant et la résistance électrique soumise à une différence de potentiel constante est également régie par une fonction de proportionnalité inverse. Cette fonction est connue sous le nom de loi d’Ohm (V=I×R).