How to Factor Polynomials (Polynomial Factoring) -

Sur cette page, nous expliquons comment factoriser tout type de polynôme. Nous verrons d’abord comment factoriser un polynôme avec la règle de Ruffini, puis nous passerons à la façon dont sont factorisés les polynômes sans terme indépendant, puis nous analyserons les factorisations de polynômes de racines avec fractions et, enfin, les cas particuliers de factorisations ( identités notables, factorisation par regroupement, trinômes, etc.). Toutes les explications sont faites avec des exemples et, en plus, à la fin vous pourrez vous entraîner avec les exercices résolus étape par étape pour factoriser les polynômes.

Qu’est-ce que la factorisation polynomiale ?

La factorisation polynomiale est une technique utilisée en mathématiques pour décomposer un polynôme en produit de facteurs.

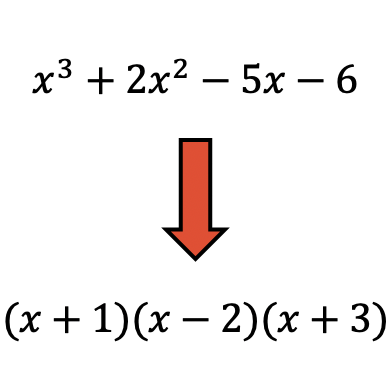
factorisation de polynômes (factorisation de polynômes)

La factorisation de polynômes est très utile car il est plus facile d’effectuer des opérations avec des polynômes factorisés.

Maintenant que nous savons ce qu’est la factorisation des polynômes, voyons comment les polynômes sont factorisés.

Comment factoriser des polynômes avec la règle de Ruffini

Évidemment, pour comprendre comment factoriser un polynôme avec la règle de Ruffini, il faut d’abord savoir appliquer la règle de Ruffini . Nous vous laissons donc ce lien au cas où vous souhaiteriez d’abord revoir à quoi ressemblait la procédure.

Pour factoriser un polynôme, les étapes suivantes doivent être suivies :

Les racines du polynôme sont calculées selon la règle de Ruffini.
Chaque racine trouvée du type x=a est exprimée sous la forme d’un facteur (xa).
Le polynôme factorisé est le produit de tous les facteurs trouvés multipliés par le coefficient du terme de degré le plus élevé du polynôme non pondéré.

Afin que vous puissiez voir comment cela se fait et mieux comprendre la procédure de factorisation des polynômes, vous trouverez ci-dessous un exemple concret expliqué étape par étape :

Factoriser le polynôme suivant :

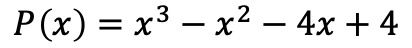
La première chose à faire est de calculer les racines ou les zéros du polynôme. Pour ce faire, nous devons trouver les diviseurs du terme indépendant du polynôme , qui sont dans ce cas ±1, ±2 et ±4.

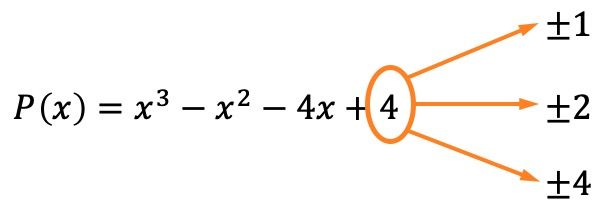
Or on sait, grâce au théorème du reste et des facteurs, que si le reste de la division du polynôme par l’une de ces valeurs est égal à 0, cela signifie que ladite valeur est une racine du polynôme.

Il faut donc diviser le polynôme par chacun des diviseurs du terme indépendant avec la règle de Ruffini et voir dans quels cas le reste est nul.

On commence par exemple par appliquer la règle de Ruffini avec

$x=+1:$

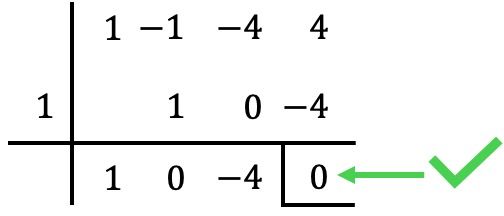
Dans ce cas, le reste (ou résidu) de la division est nul, donc

$x=1$ C’est une racine du polynôme. ✅

Parfait, on a déjà une racine du polynôme, il ne reste plus qu’à déterminer les autres racines restantes. Pour ce faire, on utilise la règle de Ruffini avec un autre diviseur du terme indépendant, par exemple

$x=-1.$ De plus, il n’est pas nécessaire d’utiliser la méthode de Ruffini avec le polynôme entier, mais nous pouvons continuer là où nous nous sommes arrêtés à l’étape précédente :

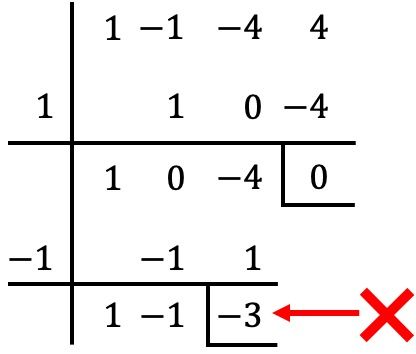
factoriser des polynômes étape par étape

Cependant, dans ce cas, lorsque l’on divise par

$x=-1$ le reste obtenu est différent de 0, donc $x=-1$ Ce n’est pas une racine du polynôme. ❌

Il faut donc essayer une autre valeur, par exemple on fait la règle de Ruffini avec

$x=+2:$

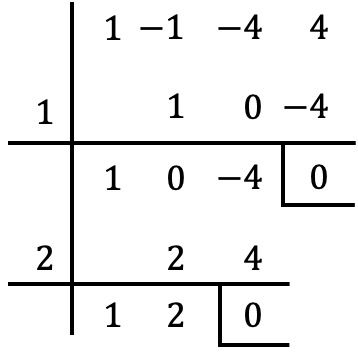
factoriser les polynômes étape par étape

Dans ce cas, nous obtenons à nouveau un reste nul, donc

$x=2$ C’est aussi une racine du polynôme.

Et nous continuons à appliquer la même procédure. Maintenant, nous vérifions si

$x=-2$ est-ce une racine du polynôme ou non :

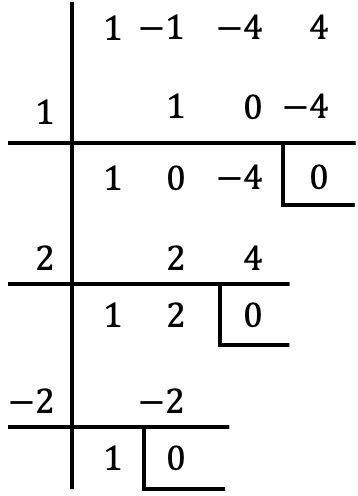
En divisant par

$x=-2$ Avec la règle de Ruffini on obtient un reste nul, donc $x=-2$ est une racine ou un zéro du polynôme.

On ne peut donc plus continuer à appliquer la règle de Ruffini, on a donc déjà trouvé toutes les racines du polynôme, qui sont :

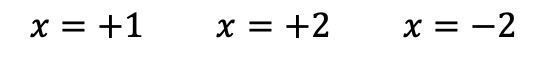
Une fois que nous avons déterminé toutes les racines du polynôme, nous pouvons le factoriser. Pour ce faire, il suffit d’exprimer chaque racine

$x=a$ sous la forme d’un facteur du type $(x-a)$ , c’est-à-dire que pour chaque racine il faut mettre une parenthèse avec un $x$ et la racine a changé de signe :

Et maintenant que nous avons toutes les racines exprimées sous forme de facteurs, il faut multiplier toutes les parenthèses par le coefficient du terme du plus haut degré du polynôme d’origine :

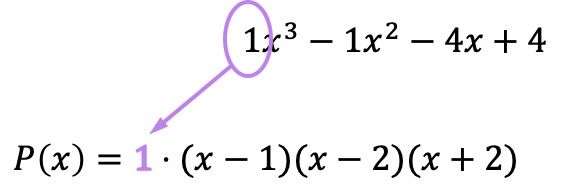
factoriser les polynômes coefficient le plus haut degré

Bien que dans ce cas le coefficient soit 1 et n’affecte donc pas le résultat, il est important de rappeler de faire cette multiplication. Puisque si ledit coefficient était différent de 1, le polynôme factorisé changerait et, par conséquent, en ne saisissant pas le nombre, nous ferions une erreur dans la factorisation du polynôme.

En bref, le polynôme factorisé est :

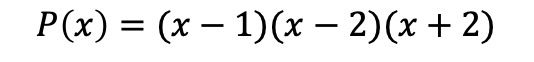
Factorisation de polynômes sans terme indépendant

Nous venons de voir que le terme indépendant est important pour la factorisation des polynômes, puisqu’il permet d’identifier les racines possibles du polynôme. Cependant, comment factoriser un polynôme qui n’a pas de terme indépendant ?

Pour factoriser un polynôme sans terme indépendant , il faut d’abord extraire le facteur commun du polynôme, puis extraire les racines du polynôme sans le facteur commun en utilisant la règle de Ruffini.

Écrit ainsi, cela peut paraître un peu compliqué, nous allons donc résoudre un exemple étape par étape afin que vous puissiez voir comment factoriser un polynôme avec un facteur commun :

Effectuez la décomposition factorielle du polynôme suivant :

$P(x) = x^4-3x^3-x^2+3x$

Comme vous pouvez le voir, le polynôme du problème n’a pas de terme indépendant, nous devons donc prendre le facteur commun du polynôme. Si on regarde bien, tous les éléments du polynôme ont au moins un

$x,$ donc le facteur commun est le $x.$ Par conséquent, lors de l’extraction du facteur commun du polynôme, nous nous retrouvons avec l’expression suivante :

$P(x) = x\left(x^3-3x^2-x+3\right)$

Et une fois qu’on a extrait le facteur commun du polynôme, on applique la règle de Ruffini pour calculer les racines du polynôme regroupées entre parenthèses (avec la procédure que l’on a vue dans la section précédente) :

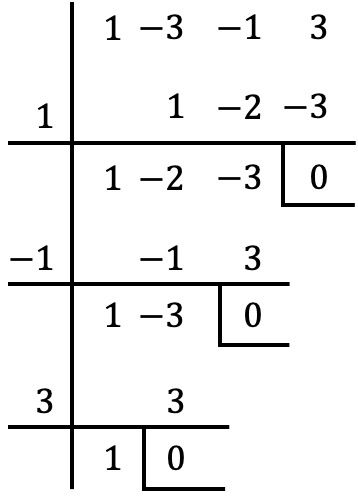
polynômes factoriels sans terme indépendant

Ainsi, les racines ou zéros du polynôme entre parenthèses sont :

$\bm{x=+1 \qquad x=-1 \qquad x=+3}$

Par conséquent, pour factoriser le polynôme, il suffit de remplacer le polynôme entre parenthèses par ses racines sous forme de facteurs (comme expliqué dans la section ci-dessus) :

$\begin{array}{c}P(x) = x\left(x^3-3x^2-x+3\right) \\[2ex]\color{red} \bm{\downarrow} \\[2ex] \bm{P(x) = x(x-1)(x+1)(x-3)}\end{array}$

Et de cette manière nous avons déjà factorisé le polynôme qui n’avait pas de terme de degré 0. Notez que la seule différence est qu’il faut d’abord extraire un facteur commun, mais toutes les étapes suivantes sont exactement identiques.

D’un autre côté, il faut savoir que

$x=0$ C’est aussi une racine du polynôme, puisque lorsque l’on extrait le facteur commun, cela implique que l’une des racines du polynôme est $x=0.$ Ainsi, toutes les racines du polynôme sont les suivantes :

$\bm{x= 0 \qquad x=+1 \qquad x=-1 \qquad x=+3}$

En fait, le polynôme doit avoir autant de racines que son degré l’indique. Dans ce cas le polynôme est de degré 4 et possède donc 4 racines.

Factorisation de polynômes avec des racines rationnelles

Jusqu’à présent, nous avons vu des exemples de factorisations de polynômes avec des racines entières, cependant, un polynôme peut aussi avoir des racines rationnelles, c’est-à-dire avec des fractions. Voyons comment ce type de factorisations polynomiales est résolu avec un exemple :

Factoriser le polynôme incomplet suivant :

$P(x) = 4x^3-7x+3$

Comme toujours, on utilise la règle de Ruffini avec les diviseurs du terme indépendant pour tenter de déterminer les racines du polynôme :

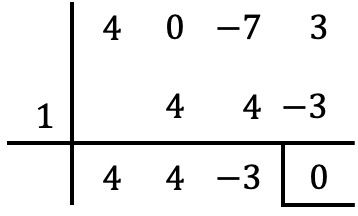
Factorisation de polynômes avec des racines rationnelles

Mais on ne peut pas calculer plus de racines avec Ruffini, car si l’on essaie de faire Ruffini avec tous les autres nombres diviseurs du terme indépendant on obtient un reste autre que zéro.

Nous nous retrouvons donc dans une situation où ce n’est qu’avec

$x=1$ le reste de la division est équivalent à 0, cela signifie que le polynôme peut avoir des racines fractionnaires. Pour déterminer ces racines, nous pourrions appliquer Ruffini avec des fractions, cependant, il est très facile de faire des erreurs dans les calculs et c’est pourquoi dans ces cas, on fait généralement ce qui suit :

Lorsque nous ne pouvons pas continuer à appliquer la règle de Ruffini avec des racines entières, nous devons mettre le dernier polynôme obtenu égal à 0 et résoudre l’équation résultante. Ainsi, les racines du polynôme seront les valeurs trouvées à partir de l’équation.

En revanche, si l’équation n’a pas de solution, cela signifie que le polynôme n’a plus de racines et, par conséquent, ne peut être complètement factorisé.

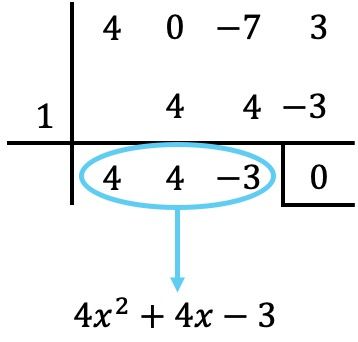
Nous fixons donc le polynôme quotient égal à zéro :

$4x^2+4x-3=0$

Et nous utilisons la formule de l’équation quadratique pour résoudre l’équation résultante :

$x= \cfrac{-b \pm \sqrt{b^2-4ac}}{2a}$

$x= \cfrac{-4 \pm \sqrt{4^2-4\cdot 4\cdot (-3)}}{2\cdot 4}= \cfrac{-4\pm \sqrt{16+48}}{8} = \cfrac{-4 \pm\sqrt{64}}{8}$

$\displaystyle x = \cfrac{-4 \pm 8}{8} = \begin{cases} \cfrac{-4+8}{8} = \cfrac{4}{8} = \cfrac{1}{2} \\[4ex]\cfrac{-4-8}{8} = \cfrac{-12}{8} = -\cfrac{3}{2} \end{cases}$

Les racines du polynôme sont donc :

$x=+1 \qquad x=\cfrac{1}{2} \qquad x=-\cfrac{3}{2}$

Le polynôme a donc des racines sous forme de fractions.

Et une fois que nous connaissons toutes les racines du polynôme, nous pouvons facilement trouver le polynôme factorisé en exprimant chaque racine

$x=a$ sous la forme d’un facteur du type $(x-a)$ , c’est-à-dire que pour chaque racine il faut mettre une parenthèse avec un $x$ et la racine a changé de signe :

$\displaystyle P(x)= 4\left(x-1\right)\left(x-\frac{1}{2}\right)\left(x+\frac{3}{2}\right)$

N’oubliez pas que pour factoriser un polynôme, vous devez également multiplier ses facteurs par le coefficient du terme du plus haut degré du polynôme non factorisé, qui dans ce cas est 4.

Cas particuliers de factorisation de polynômes

Normalement, la règle de Ruffini (ou division synthétique) est utilisée pour factoriser un polynôme, comme expliqué ci-dessus. Mais selon le polynôme du problème, vous pouvez parfois effectuer une factorisation polynomiale plus rapidement. Nous verrons ci-dessous chacun de ces cas particuliers.

Factoriser les identités notables

Si l’on voit qu’un polynôme correspond à une identité notable (ou un produit notable) il est très simple de le factoriser. Cependant, pour pouvoir faire cela vous devez maîtriser les formules des identités notables , sinon je vous recommande de jeter un oeil à ce lien où vous trouverez non seulement les formules, mais vous pourrez aussi voir des exemples de notables. identités et vous pouvez même pratiquer avec elles des exercices résolus étape par étape.

Différence de carrés

Comme vous le savez bien, la formule de l’identité notable de la différence des carrés est la suivante :

$a^2-b^2=(a+b)\cdot (a-b)$

Par conséquent, si nous trouvons un polynôme qui répond à l’expression

$a^2-b^2$ peut être pris en compte directement.

Regardez l’exemple suivant dans lequel une différence de carrés est prise en compte :

$x^2-9 = (x+3)(x-3)$

En revanche, les racines du polynôme sont :

$x=-3 \qquad x=+3$

Autres exemples de binômes de factorisation qui sont des différences de carrés :

$x^2-4=(x+2)(x-2) \quad \longrightarrow \quad \text{ra\'ices: } x=-2, +2$

$x^2-16=(x+4)(x-4) \quad \longrightarrow \quad \text{ra\'ices: } x=-4, +4$

$x^2-25=(x+5)(x-5) \quad \longrightarrow \quad \text{ra\'ices: } x=-5, +5$

Carré d’addition et de soustraction

Vous devriez déjà connaître les formules des 2 principales identités notables restantes : le carré d’addition et le carré de soustraction.

Somme Carré

$a^2+2ab+b^2 = (a+b)^2$

Carré de soustraction

$a^2-2ab+b^2= (a-b)^2$

Ainsi, si l’on se rend compte qu’un polynôme correspond à l’une de ces deux identités notables, on peut le factoriser directement. Regardez les exemples suivants :

$x^2+6x+9 = (x+3)^2$

Racine double :

$x=-3$

$x^2-8x+16 = (x-4)^2$

Racine double :

$x=4$

L’identification de ces types de produits notables est un peu plus difficile. Une astuce consiste à vérifier si le terme indépendant du polynôme est le carré d’un certain nombre, et si le terme de degré le plus élevé est le carré d’un monôme (généralement

$x$ ), dans ce cas, il suffit de vérifier qu’il est vrai que $2ab$ est égal au terme du diplôme intermédiaire.

Par exemple, si nous avons le polynôme suivant :

$x^2+10x+25$

Dans ce cas, il ne peut s’agir que du carré d’une somme, car tous les éléments du polynôme sont positifs. Donc la variable

$b$ de la formule doit être 5, puisque c’est la racine du terme indépendant, et la variable $a$ ça doit être $x$ , puisque c’est la racine du terme de mai degré.

$a=\sqrt{x^2} = x$

$b=\sqrt{25} = 5$

Il ne nous reste plus qu’à prouver que la formule du carré de la somme est remplie avec le terme de degré intermédiaire :

$2ab = 10x \ \color{blue} \bm{?}$

$2ab = 2\cdot x \cdot 5 = 10 x$ ✅

La formule du produit notable est satisfaite, donc le polynôme factorisé est :

$x^2+10x+25 = (x+5)^2$

Et la racine de ce polynôme est

$x=-5,$ qui est une racine double car son facteur est au carré (il est répété deux fois).

Vous trouverez ci-dessous d’autres exemples de factorisation de trinômes carrés parfaits :

$x^2-4x+4=(x-2)^2 \quad \longrightarrow \quad \text{ra\'iz doble: } x=+2$

$x^2+14x+49=(x+7)^2 \quad \longrightarrow \quad \text{ra\'iz doble: } x=-7$

$9x^2-12x+4=(3x-2)^2 \quad \longrightarrow \quad \text{ra\'iz doble: } x=+\cfrac{2}{3}$

Factorisation des trinômes du deuxième degré

Comme nous venons de le voir, il existe parfois des trinômes qui sont des carrés parfaits et ceux-ci peuvent être directement factorisés avec les formules d’identités notables. Mais la plupart des trinômes ne sont pas des produits notables, alors comment factoriser ces cas de polynômes ?

Pour factoriser un polynôme du deuxième degré, il n’est pas nécessaire d’appliquer la méthode de Ruffini, il suffit de fixer le polynôme égal à zéro et de résoudre l’équation du deuxième degré résultante. Les solutions de l’équation seront donc les racines du polynôme.

Par exemple, si l’on nous demande de factoriser le polynôme de degré 2 suivant :

$P(x) = x^2+2x-15$

Au lieu d’utiliser Ruffini, nous fixons le polynôme égal à 0 :

$x^2+2x-15=0$

Et maintenant, nous utilisons la formule de l’équation du 2ème degré pour trouver les solutions de l’équation :

$x= \cfrac{-b \pm \sqrt{b^2-4ac}}{2a}$

$x= \cfrac{-2 \pm \sqrt{2^2-4\cdot 1\cdot (-15)}}{2\cdot 1}= \cfrac{-2\pm \sqrt{4+60}}{2} = \cfrac{-2 \pm\sqrt{64}}{2}$

$\displaystyle x = \cfrac{-2 \pm 8}{2} = \begin{cases} \cfrac{-2+8}{2} = \cfrac{6}{2} = 3 \\[4ex]\cfrac{-2-8}{2} = \cfrac{-10}{2} = -5 \end{cases}$

Les racines du polynôme sont donc :

$x=3 \qquad x=-5$

Et finalement, la factorisation polynomiale est :

$P(x) =(x-3)(x+5)$

Factorisation de trinômes du quatrième degré avec des exposants pairs

Comme dans le cas précédent, pour factoriser un polynôme du quatrième degré avec des exposants pairs, nous devons fixer le polynôme égal à zéro et résoudre l’équation bicarrée. Pour que les valeurs trouvées correspondent aux racines du polynôme.

A titre d’exemple, nous allons factoriser le polynôme de degré 4 suivant :

$P(x) =x^4-5x^2+4$

Tout d’abord, nous fixons le polynôme égal à zéro :

$x^4-5x^2+4=0$

Nous devons maintenant résoudre l’équation bicarrée. Pour ce faire, nous effectuons un changement de variable :

$x^2=t$

$t^2-5t+4=0$

On résout l’équation quadratique avec la formule :

$t= \cfrac{-b \pm \sqrt{b^2-4ac}}{2a}$

$t= \cfrac{-(-5) \pm \sqrt{(-5)^2-4\cdot 1\cdot 4}}{2\cdot 1}= \cfrac{5\pm \sqrt{25-16}}{2} = \cfrac{5 \pm\sqrt{9}}{2}$

$\displaystyle t = \cfrac{5 \pm 3}{2} = \begin{cases} \cfrac{5+3}{2} = \cfrac{8}{2} = 4 \\[4ex]\cfrac{5-3}{2} = \cfrac{2}{2} = 1 \end{cases}$

On annule le changement de variable pour calculer les racines :

$x^2=t$

$x^2=4$

$x=\sqrt{4}$

$x=\pm 2$

$x^2=1$

$x=\sqrt{1}$

$x=\pm 1$

Les racines du polynôme sont donc :

$x=+2 \qquad x=-2 \qquad x=+1 \qquad x=-1$

Et une fois que l’on connaît les racines ou les zéros du polynôme, on le factorise en exprimant algébriquement ses racines sous forme de facteurs :

$P(x) =(x-1)(x+1)(x-2)(x+2)$

Factorisation de polynômes par regroupement

Dans certains cas très particuliers, une formule peut être utilisée pour factoriser un type de polynôme très particulier.

Si on a un polynôme de la forme suivante :

$x^2-ax- bx+ab$

Nous pouvons simplifier le polynôme en supprimant le facteur commun :

$x^2-ax- bx+ab = x(x-a)-b(x-a)$

Et le polynôme peut être encore simplifié en extrayant le facteur commun une seconde fois :

$x(x-a)-b(x-a) =(x-a)\cdot (x-b)$

De cette façon, nous avons pu factoriser le polynôme sans appliquer Ruffini ou toute autre méthode. Et les racines dudit polynôme seraient :

$x=a \qquad x=b$

Voyons maintenant cette méthode avec un exemple numérique :

$x^2-3x-2x+6$

Tout d’abord, nous retirons le facteur commun avec

$x$ et avec 2 :

$x^2-3x-2x+6 = x(x-3)-2(x-3)$

Et comme maintenant

$(x-3)$ est un facteur commun du polynôme, on extrait le facteur commun de $(x-3):$

$x(x-3)-2(x-3)=(x-3)\cdot (x-2)$

Les racines du polynôme sont donc :

$x=3 \qquad x=2$

Cette méthode est également appelée factorisation de polynômes par extraction de double facteur commun. Bien qu’il s’agisse d’une procédure très rapide, nous ne recommandons pas de réaliser ce type de factorisation car des erreurs sont fréquemment signalées lors de la factorisation avec cette méthode. De plus, comme nous l’avons vu ci-dessus, un polynôme de degré 2 peut également être factorisé en résolvant une simple équation quadratique. Bref, rien ne se passe si vous ne comprenez pas bien cette méthode.

Enfin, il convient de noter qu’il existe encore d’autres méthodes de factorisation polynomiale plus complexes, comme l’algorithme LLL, la méthode de Kronecker et la méthode Trager, qui ne sont pas expliquées ici en raison de leur difficulté mathématique.

Exercices résolus sur la factorisation des polynômes

Une fois que vous avez vu tous les types de polynômes de factorisation, nous vous recommandons de vous entraîner à essayer de résoudre des exercices. C’est pourquoi nous avons préparé ci-dessous plusieurs exercices résolus étape par étape pour la factorisation de polynômes. N’oubliez pas que si vous avez des questions, vous pouvez les écrire dans les commentaires et nous y répondrons rapidement.

Exercice 1

Effectuer la factorisation du polynôme de degré 3 suivant :

$P(x)=x^3-3x^2-6x+8$

Voir la solution

C’est un polynôme complet, ordonné, du troisième degré et à terme indépendant. Par conséquent, nous appliquons la méthode de Ruffini pour déterminer les racines du polynôme :

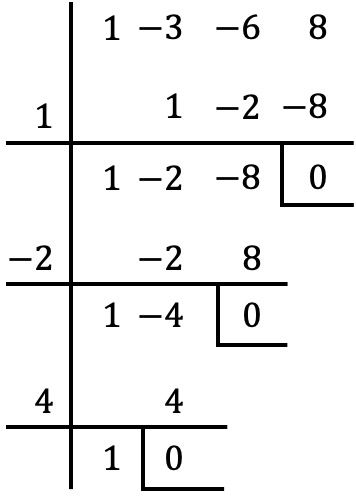
exercices étape par étape pour factoriser des polynômes

Les racines du polynôme sont donc les suivantes :

$x=+1 \qquad x=-2 \qquad x=+4$

La factorisation polynomiale est donc :

$P(x)= 1 \cdot (x-1)\cdot (x+2) \cdot (x-4)$

$\bm{P(x)= (x-1)(x+2)(x-4)}$

Exercice 2

Calculez la factorisation du polynôme de degré 4 suivant :

$P(x)=x^4+x^3-7x^2-x+6$

Voir la solution

C’est un polynôme du quatrième degré et avec un terme indépendant, on utilise donc la méthode de Ruffini pour trouver les racines du polynôme :

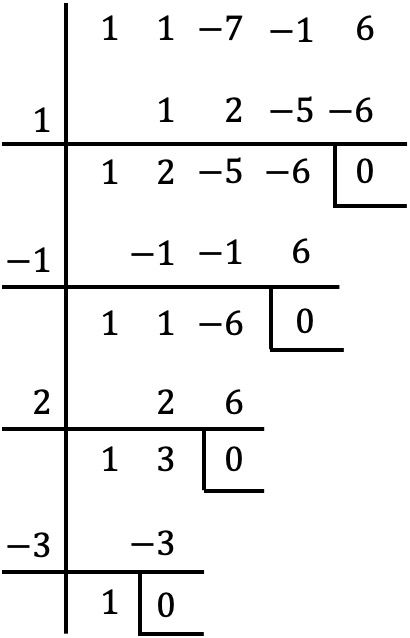
exercices de factorisation polynomiale pdf

Les racines du polynôme sont donc :

$x=+1 \qquad x=-1 \qquad x=2 \qquad x=-3$

Et lorsque l’on factorise le polynôme, il nous reste :

$P(x)= 1 \cdot (x-1)\cdot (x+1)\cdot (x-2) \cdot (x+3)$

$\bm{P(x)= (x-1)(x+1)(x-2)(x+3)}$

Exercice 3

Trouvez la factorisation du polynôme du quatrième degré suivant :

$P(x)=x^4-2x^3-13x^2-10x$

Voir la solution

Dans ce cas le polynôme n’a pas de terme indépendant, il faut donc d’abord extraire un facteur commun :

$P(x)=x(x^3-2x^2-13x-10)$

Maintenant que nous avons pris le facteur commun de x, nous calculons les racines ou les zéros du polynôme entre parenthèses en utilisant la méthode de Ruffini :

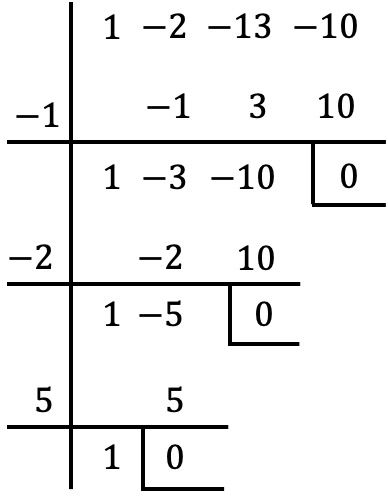
factorisation des polynômes de Ruffini exercices résolus pdf

Ainsi les racines du polynôme sont celles que nous avons trouvées par la méthode de Ruffini plus x=0 du facteur commun :

$x=0 \qquad x=-1 \qquad x=-2 \qquad x=5$

Et enfin, en décomposant le polynôme en facteurs on obtient l’expression suivante :

$P(x)= 1 \cdot x \cdot (x+1)\cdot (x+2)\cdot (x-5)$

$\bm{P(x)= x(x+1)(x+2)(x-5)}$

Exercice 4

Transformez le polynôme du troisième degré suivant en facteurs :

$P(x)=6x^3+25x^2+21x-10$

Voir la solution

Ce polynôme a un terme indépendant, on calcule donc ses racines avec l’algorithme de Ruffini :

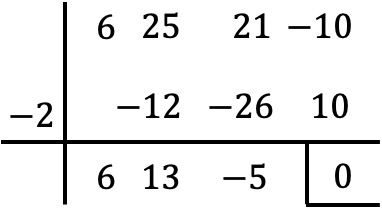
polynômes factoriels de degré 3 en ligne 2

Cependant, lorsque nous atteignons ce point, nous ne pouvons pas continuer à appliquer la règle de Ruffini, car sans autre entier, le reste de la division est nul.

Par conséquent, nous fixons le polynôme obtenu égal à zéro :

$6x^2+13x-5=0$

Et nous appliquons la formule des équations quadratiques pour résoudre l’équation résultante :

$x= \cfrac{-b \pm \sqrt{b^2-4ac}}{2a}$

$x= \cfrac{-13 \pm \sqrt{13^2-4\cdot 6\cdot (-5)}}{2\cdot 6}= \cfrac{-13\pm \sqrt{169+120}}{12} = \cfrac{-13 \pm\sqrt{289}}{12}$

$\displaystyle x = \cfrac{-13 \pm 17}{12} = \begin{cases} \cfrac{-13+17}{12} = \cfrac{4}{12} = \cfrac{1}{3} \\[4ex]\cfrac{-13-17}{12} = \cfrac{-30}{12} = -\cfrac{5}{2} \end{cases}$

Les racines ou zéros du polynôme sont donc :

$x=-2 \qquad x=\cfrac{1}{3} \qquad x=-\cfrac{5}{2}$

Donc la factorisation du polynôme doit se faire avec des fractions :

$\displaystyle P(x)= 6\left(x+2\right)\left(x-\frac{1}{3}\right)\left(x+\frac{5}{2}\right)$

Exercice 5

Déterminer la factorisation du polynôme de degré 6 suivant :

$P(x)=x^6-3x^5+14x^3-12x^2$

Voir la solution

Le polynôme du problème n’a pas de terme indépendant, nous devons donc d’abord extraire le facteur commun, qui dans ce cas est

$x^2:$

$P(x)=x^2(x^4-3x^3+14x-12)$

Et une fois qu’on a retiré le facteur commun du polynôme, on retrouve les racines du polynôme entre parenthèses grâce à la règle de Ruffini :

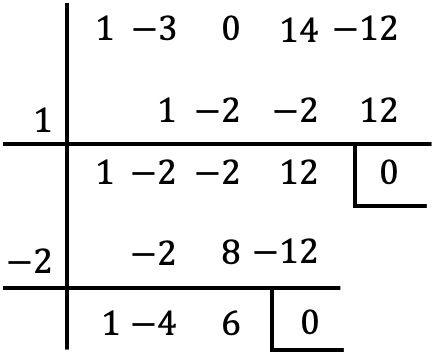
Mais lorsque nous arrivons à cette étape, nous ne pouvons pas continuer à avancer, car sans autre entier, le reste est égal à zéro.

Nous mettons donc le polynôme obtenu égal à zéro :

$x^2-4x+6=0$

Et on résout l’équation du deuxième degré avec la formule :

$x= \cfrac{-b \pm \sqrt{b^2-4ac}}{2a}$

$x= \cfrac{-(-4) \pm \sqrt{(-4)^2-4\cdot 1\cdot 6}}{2\cdot 1}= \cfrac{4\pm \sqrt{16-24}}{2} = \cfrac{4 \pm\sqrt{-8}}{2} \ \color{red} \bm{\times}$

Il n’y a pas de racines des nombres négatifs, donc l’équation n’a pas de solution, ce qui signifie que nous ne pouvons pas trouver plus de racines du polynôme. Autrement dit, le polynôme n’est pas complètement factorisable.

Cependant, les racines que nous avons pu retrouver sont :

$x=0 \qquad x=0 \qquad x=1 \qquad x=-2$

Notez que la racine

$x=0$ est répété deux fois car nous avons supprimé le facteur commun de $x^2,$ et comme il est au carré, cela implique que c’est une racine double.

En conclusion, le polynôme factorisé sera le produit de toutes les racines trouvées exprimées sous forme de facteurs

$(x-a)$ multiplié par le polynôme obtenu à partir de la règle de Ruffini qui n’a pas pu être davantage pris en compte :

$P(x)= 1 \cdot x^2 \cdot (x-1)\cdot (x+2)\cdot (x^2-4x+6)$

$\bm{P(x)= x^2(x-1)(x+2)(x^2-4x+6)}$

Exercice 6

Effectuez les factorisations de tous les polynômes suivants :

$\text{A)} \ P(x)=x^2 + 12x+36$

$\text{B)} \ Q(x)=x^2 -64$

$\text{C)} \ R(x)=x^2 - 18x+81$

$\text{D)} \ S(x)=x^2+10x+24$

Voir la solution

Le polynôme de la section A) correspond à une identité notable, notamment le carré de la somme. Sa factorisation est donc :

$P(x)=x^2 + 12x+36 = \bm{(x+6)^2}$

Le polynôme de la section B) est aussi un produit notable, en particulier c’est la différence des carrés, donc :

$Q(x)=x^2 -64 = \bm{(x+8)(x-8)}$

De la même manière, le polynôme de la section C) est une égalité notable, en particulier il consiste en le carré d’une soustraction. Sa factorisation est donc :

$R(x)=x^2 - 18x+81 = \bm{(x-9)^2}$

Enfin, le polynôme de la partie D) n’est pas une identité notable. Il faut donc mettre le polynôme égal à 0 et résoudre l’équation résultante pour trouver ses racines :

$x^2+10x+24 =0$

On utilise la formule de l’équation du deuxième degré :

$x= \cfrac{-b \pm \sqrt{b^2-4ac}}{2a}$

$x= \cfrac{-10 \pm \sqrt{10^2-4\cdot 1\cdot 24}}{2\cdot 1}= \cfrac{-10\pm \sqrt{100-96}}{2} = \cfrac{-10 \pm\sqrt{4}}{2}$

$\displaystyle x = \cfrac{-10 \pm 2}{2} = \begin{cases} \cfrac{-10+2}{2} = \cfrac{-8}{2} = -4 \\[4ex]\cfrac{-10-2}{2} = \cfrac{-12}{2} = -6\end{cases}$

Les racines du polynôme D) sont donc :

$x=-4 \qquad x=-6$

Et finalement, le résultat de la factorisation polynomiale est :

$\bm{S(x)=(x+4)(x+6)}$

Qu’est-ce que la factorisation polynomiale ?

Comment factoriser des polynômes avec la règle de Ruffini

Factorisation de polynômes sans terme indépendant

Factorisation de polynômes avec des racines rationnelles

Cas particuliers de factorisation de polynômes

Factoriser les identités notables

Différence de carrés

Carré d’addition et de soustraction

Factorisation des trinômes du deuxième degré

Factorisation de trinômes du quatrième degré avec des exposants pairs

Factorisation de polynômes par regroupement

Exercices résolus sur la factorisation des polynômes

Exercice 1

Exercice 2

Exercice 3

Exercice 4

Exercice 5

Exercice 6

Leave a Comment Cancel Reply