Matrices similaires ou similaires

Sur cette page, vous trouverez l’explication des matrices similaires, également appelées matrices similaires. De plus, nous vous montrons un exemple clair de deux matrices similaires et toutes les propriétés de ce type de matrices afin que vous n’ayez aucun doute. Enfin, vous pourrez même voir comment ils sont liés à des matrices congruentes.

Que sont les matrices similaires (ou similaires) ?

La définition des matrices similaires est la suivante :

deux matrices

$A$ et $B$ sont semblables (ou semblables) s’il existe une matrice $P$ avec laquelle la condition suivante est remplie :

$P^{-1}AP = B$

Ou équivalent:

$AP = PB$

En fait, la matrice

$P$ agit comme une matrice de changement de base. Par conséquent, ce que cette équation signifie, c’est que la matrice $A$ peut être exprimée dans une autre base ( $P$ ), ce qui donne lieu à la matrice $B$ .

Ce terme peut également être appelé une transformation de similarité , puisque nous transformons en fait la matrice

$A$ dans la matrice $B$ .

Evidemment la matrice

$P$ il doit s’agir d’une matrice régulière ou non dégénérée (déterminant non nul).

Par contre, on peut indiquer que deux matrices sont semblables avec l’expression suivante :

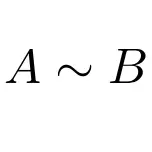
explication de matrices similaires ou similaires

Cette classe de matrices est plus importante qu’il n’y paraît pour l’algèbre linéaire. Ils sont principalement utilisés pour les matrices diagonalisables, car la procédure de diagonalisation de toute matrice est basée sur le concept de similarité matricielle.

En fait, le processus de diagonalisation d’une matrice consiste à calculer une matrice similaire qui, en même temps, est une matrice diagonale. Vous pouvez voir comment c’est fait dans comment diagonaliser une matrice .

Exemple de matrices similaires ou similaires

Ensuite nous verrons un exemple de matrices similaires de dimension 2×2 pour finir d’assimiler le concept.

Les matrices carrées A et B sont similaires entre elles par la matrice inversible P :

$\displaystyle A= \begin{pmatrix}-1&2\\[1.1ex] 3&1\end{pmatrix} \qquad B= \begin{pmatrix}-5&-3\\[1.1ex] 6&5\end{pmatrix}$

$\displaystyle P= \begin{pmatrix}2&1\\[1.1ex] -1&0\end{pmatrix}$

Pour montrer que ce sont des matrices mutuellement similaires, nous devons d’abord calculer la matrice inverse de P :

$\displaystyle P^{-1}= \begin{pmatrix}0&-1\\[1.1ex] 1&2\end{pmatrix}$

Et maintenant on vérifie qu’elles sont similaires en effectuant le produit matriciel qui définit la similarité de deux matrices :

$\displaystyle P^{-1}AP = B \quad ?$

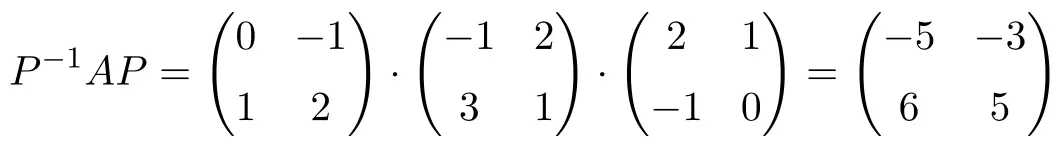
exemples de matrices 2x2 similaires ou similaires

$\displaystyle P^{-1}AP = B$ ✅

Oui, la relation de similarité est remplie, ce sont donc des matrices similaires.

Propriétés de matrices similaires

Deux matrices A et B similaires partagent les caractéristiques suivantes :

Même rang.

$rg(A)=rg(B)$

Les déterminants des deux matrices sont les mêmes.

$det(A)=det(B)$

Même traçage.

$tr(A)=tr(B)$

Mêmes valeurs propres (ou valeurs propres). Cependant, les vecteurs propres (ou vecteurs propres) sont généralement différents.

Même polynôme caractéristique et polynôme minimum.

La transposition d’une matrice est similaire à la matrice d’origine.

La matrice B peut être trouvée en appliquant des opérations élémentaires sur les lignes de la matrice A, et inversement.

Évidemment, la ressemblance est réfléchie. Autrement dit, si A est similaire à B, alors B est également similaire à A.

De plus, la similitude des matrices est également symétrique. Autrement dit, si avec la matrice P la matrice qui est similaire à A (B) peut être obtenue, la matrice qui est similaire à B (A) peut également être obtenue avec la même matrice P :

$B=P^{-1}AP$

$A=PBP^{-1}$

De plus, la similarité est transitive. Donc, si la matrice A est similaire à la matrice B et que la matrice B est similaire à la matrice C, la matrice A est également similaire à la matrice C.

$\left. \begin{array}{l}A\sim B \\[2ex] B \sim C \end{array}\right\} \longrightarrow A \sim C$

Enfin, chaque matrice est similaire à une matrice en dents de scie. Et de cette propriété on peut déduire le corollaire suivant : toute matrice carrée est semblable à une matrice triangulaire.

matrices congruentes

D’autre part, il existe également une autre relation très similaire entre les matrices mais au lieu d’être avec la matrice inverse, c’est avec la matrice transposée. Cela s’appelle la congruence .

Deux matrices A et B sont congruentes s’il existe une matrice inversible P avec laquelle l’égalité suivante est satisfaite :

$P^tAP = B$

Comme vous pouvez le voir, c’est l’analogue des matrices similaires mais avec la matrice transposée.

Que sont les matrices similaires (ou similaires) ?

Exemple de matrices similaires ou similaires

Propriétés de matrices similaires

matrices congruentes

Leave a Comment Cancel Reply