Comment diagonaliser une matrice -

Sur cette page, vous trouverez tout sur les matrices diagonalisables : ce qu’elles sont, quand elles peuvent être diagonalisées et quand elles ne le peuvent pas, la méthode pour diagonaliser les matrices, les applications et propriétés de ces matrices particulières, etc. Et vous avez même plusieurs exercices résolus étape par étape afin que vous puissiez pratiquer et comprendre parfaitement comment ils sont diagonalisés. Enfin, nous apprenons également à réaliser des diagonalisations matricielles avec le programme informatique MATLAB, car il est très fréquemment utilisé.

Qu’est-ce qu’une matrice diagonalisable ?

Comme nous le verrons ci-dessous, diagonaliser une matrice est très utile dans le domaine de l’algèbre linéaire. C’est pourquoi beaucoup se demandent… qu’est-ce que la diagonalisation d’une matrice ? Eh bien, la définition d’une matrice diagonalisable est la suivante :

Une matrice diagonalisable est une matrice carrée qui peut être transformée en matrice diagonale, c’est-à-dire une matrice remplie de zéros sauf sur la diagonale principale. La diagonalisation des matrices se décompose comme suit :

$A = PDP^{-1}$

Ou équivalent,

$D = P^{-1}AP$

Où

$A$ est la matrice à diagonaliser, $P$ est la matrice dont les colonnes sont les vecteurs propres (ou vecteurs propres) de $A$ , $P^{-1}$ sa matrice inverse et $D$ est la matrice diagonale formée par les valeurs propres (ou valeurs propres) de $A$ .

La matrice

$P$ agit comme une matrice de changement de base, donc en fait avec cette formule nous changeons la base en matrice $A$ , de sorte que la matrice devient une matrice diagonale ( $D$ ) dans la nouvelle base.

Par conséquent, la matrice

$A$ et la matrice $D$ Ce sont des matrices similaires. Et évidemment, $P$ C’est une matrice régulière ou non dégénérée.

Quand peut-on diagonaliser une matrice ?

Toutes les matrices ne sont pas diagonalisables, seules les matrices répondant à certaines caractéristiques peuvent être diagonalisées. Vous pouvez savoir si une matrice est diagonalisable de différentes manières :

Une matrice carrée d’ordre n est diagonalisable si elle possède n vecteurs propres (ou vecteurs propres) linéairement indépendants , ou en d’autres termes, si ces vecteurs forment une base. C’est parce que la matrice 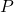$P$ , qui sert à diagonaliser une matrice, est formé par les vecteurs propres de ladite matrice. Pour savoir si les vecteurs propres sont LI, il suffit que le déterminant de la matrice 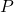$P$ est différent de 0, ce qui signifie que la matrice a le rang maximum.

$\text{si} \quad \text{det}(P)\neq 0 \ \longrightarrow \ \text{matriz diagonalizable}$

Une propriété des valeurs propres et des vecteurs propres est que les vecteurs propres de différentes valeurs propres sont linéairement indépendants. Par conséquent, si toutes les valeurs propres de la matrice sont uniques, la matrice est diagonalisable.

Une autre façon de déterminer si une matrice peut être prise en compte dans une matrice diagonale consiste à utiliser les multiplicités algébriques et géométriques. La multiplicité algébrique est le nombre de fois qu’une valeur propre (ou valeur propre) est répétée, et la multiplicité géométrique est la dimension du noyau (ou noyau) de la matrice en soustrayant la valeur propre sur sa diagonale principale. Ainsi, si pour chaque valeur propre la multiplicité algébrique est égale à la multiplicité géométrique , la matrice est diagonalisable.

$\alpha_\lambda = \text{multiplicidad algebraica} = \text{multiplicidad del valor propio}$

$m_\lambda = \text{multiplicidad geom\'etrica} = \text{dim } Ker(A-\lambda I) = n -rg(A-\lambda I)$

$\alpha_\lambda \geq m_\lambda \geq 1$

$\text{si} \quad \alpha_\lambda = m_\lambda \quad \forall \lambda \ \longrightarrow \ \text{matriz diagonalizable}$

Enfin, il existe un théorème, le théorème spectral, qui garantit la diagonalisation de matrices symétriques à nombres réels. Autrement dit, toute matrice réelle et symétrique est diagonalisable .

Comment diagonaliser une matrice

La procédure de diagonalisation d’une matrice repose sur la recherche des valeurs propres (ou valeurs propres) et des vecteurs propres (ou vecteurs propres) d’une matrice. C’est pourquoi il est important que vous maîtrisiez comment calculer les valeurs propres (ou valeurs propres) et les vecteurs propres (ou vecteurs propres) de toute matrice . Vous pouvez vous rappeler comment cela a été fait en cliquant sur le lien, où nous expliquons étape par étape comment les trouver et quelques astuces qui facilitent grandement les calculs. De plus, vous trouverez également des exercices résolus à pratiquer.

Avec la méthode suivante, vous pouvez diagonaliser une matrice de n’importe quelle dimension : 2×2, 3×3, 4×4, etc. Les étapes à suivre pour diagonaliser une matrice sont :

Obtenir les valeurs propres (ou valeurs propres) de la matrice.
Calculez le vecteur propre associé à chaque valeur propre.
Construire la matrice 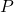$P$ , dont les colonnes sont les vecteurs propres de la matrice à diagonaliser.
Vérifiez que la matrice peut être diagonalisée (elle doit remplir une des conditions expliquées dans la section précédente).
Construire la matrice diagonale 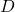$D$ , dont les éléments sont tous 0 sauf ceux de la diagonale principale, qui sont les valeurs propres trouvées à l’étape 1.

Attention : Les vecteurs propres de la matrice

$P$ peut être placé dans n’importe quel ordre, mais les valeurs propres de la matrice diagonale $D$ Ils doivent être placés dans le même ordre. Par exemple, la première valeur propre de la matrice diagonale $D$ doit être celui qui correspond au vecteur propre de la première colonne de la matrice $P$ .

Vous trouverez ci-dessous plusieurs exercices de diagonalisation matricielle étape par étape avec lesquels vous pouvez vous entraîner.

Exercices de diagonalisation matricielle résolus

Exercice 1

Diagonalisez la matrice carrée suivante de dimension 2×2 :

$\displaystyle A= \begin{pmatrix}2&2\\[1.1ex] 1&3\end{pmatrix}$

Voir la solution

Il faut d’abord déterminer les valeurs propres de la matrice A. On calcule donc l’équation caractéristique en résolvant le déterminant suivant :

$\displaystyle \text{det}(A-\lambda I)= \begin{vmatrix}2- \lambda &2\\[1.1ex] 1&3-\lambda \end{vmatrix} = \lambda^2-5\lambda +4$

Calculons maintenant les racines du polynôme caractéristique :

$\displaystyle \lambda^2-5\lambda +4=0 \ \longrightarrow \ \begin{cases} \lambda = 4 \\[2ex] \lambda = 1 \end{cases}$

Une fois les valeurs propres obtenues, on calcule le vecteur propre associé à chacune. Tout d’abord, le vecteur propre correspondant à la valeur propre 1 :

$\displaystyle (A-I)v=0$

$\displaystyle \begin{pmatrix}1&2\\[1.1ex] 1&2\end{pmatrix}\begin{pmatrix}x \\[1.1ex] y \end{pmatrix} =}\begin{pmatrix}0 \\[1.1ex] 0 \end{pmatrix}$

$\displaystyle \left.\begin{array}{l} x+2y = 0 \\[2ex] x+2y = 0\end{array}\right\} \longrightarrow \ x=-2y$

$\displaystyle v = \begin{pmatrix}-2 \\[1.1ex] 1 \end{pmatrix}$

Et puis on calcule le vecteur propre associé à la valeur propre 4 :

$\displaystyle (A-4I)v=0$

$\displaystyle \begin{pmatrix}-2&2\\[1.1ex] 1&-1\end{pmatrix}\begin{pmatrix}x \\[1.1ex] y \end{pmatrix} =}\begin{pmatrix}0 \\[1.1ex] 0 \end{pmatrix}$

$\displaystyle \left.\begin{array}{l} -2x+2y = 0 \\[2ex] x-y = 0\end{array}\right\} \longrightarrow \ y=x$

$\displaystyle v = \begin{pmatrix}1 \\[1.1ex] 1 \end{pmatrix}$

Nous construisons la matrice

$P$ , formé par les vecteurs propres de la matrice :

$\displaystyle P = \begin{pmatrix}-2&1 \\[1.1ex] 1&1 \end{pmatrix}$

Puisque toutes les valeurs propres sont différentes, la matrice A est diagonalisable. Ainsi la matrice diagonale correspondante est celle qui possède les valeurs propres sur la diagonale principale :

$\displaystyle D= \begin{pmatrix}1&0\\[1.1ex] 0&4\end{pmatrix}$

N’oubliez pas que les valeurs propres doivent être placées dans le même ordre que les vecteurs propres sont placés dans la matrice

$P$ .

En conclusion, la matrice de changement de base et la matrice diagonalisée sont :

$\displaystyle P = \begin{pmatrix}-2&1 \\[1.1ex] 1&1 \end{pmatrix} \qquad D= \begin{pmatrix}1&0\\[1.1ex] 0&4\end{pmatrix}$

Exercice 2

Diagonalisez la matrice carrée d’ordre 2 suivante :

$\displaystyle A= \begin{pmatrix}3&4\\[1.1ex] -1&-2\end{pmatrix}$

Voir la solution

Il faut d’abord déterminer les valeurs propres de la matrice A. On calcule donc l’équation caractéristique en résolvant le déterminant suivant :

$\displaystyle \text{det}(A-\lambda I)= \begin{vmatrix}3- \lambda &4\\[1.1ex] -1&-2-\lambda \end{vmatrix} = \lambda^2-\lambda -2$

Calculons maintenant les racines du polynôme caractéristique :

$\displaystyle \lambda^2-\lambda -2=0 \ \longrightarrow \ \begin{cases} \lambda = -1 \\[2ex] \lambda = 2 \end{cases}$

Une fois les valeurs propres obtenues, on calcule le vecteur propre associé à chacune. Tout d’abord, le vecteur propre correspondant à la valeur propre -1 :

$\displaystyle (A+I)v=0$

$\displaystyle \begin{pmatrix}4&4\\[1.1ex] -1&-1\end{pmatrix}\begin{pmatrix}x \\[1.1ex] y \end{pmatrix} =}\begin{pmatrix}0 \\[1.1ex] 0 \end{pmatrix}$

$\displaystyle \left.\begin{array}{l} 4x+4y = 0 \\[2ex] -x-y = 0\end{array}\right\} \longrightarrow \ x=-y$

$\displaystyle v = \begin{pmatrix}-1 \\[1.1ex] 1 \end{pmatrix}$

Et puis on calcule le vecteur propre associé à la valeur propre 2 :

$\displaystyle (A-2I)v=0$

$\displaystyle \begin{pmatrix}1&4\\[1.1ex] -1&-4\end{pmatrix}\begin{pmatrix}x \\[1.1ex] y \end{pmatrix} =}\begin{pmatrix}0 \\[1.1ex] 0 \end{pmatrix}$

$\displaystyle \left.\begin{array}{l} x+4y = 0 \\[2ex] -x-4y = 0\end{array}\right\} \longrightarrow \ x=-4y$

$\displaystyle v = \begin{pmatrix}-4 \\[1.1ex] 1 \end{pmatrix}$

Nous construisons la matrice

$P$ , formé par les vecteurs propres de la matrice :

$\displaystyle P = \begin{pmatrix}-1&-4 \\[1.1ex] 1&1 \end{pmatrix}$

Puisque toutes les valeurs propres sont différentes les unes des autres, la matrice A est diagonalisable. Ainsi la matrice diagonale correspondante est celle qui contient les valeurs propres sur la diagonale principale :

$\displaystyle D= \begin{pmatrix}-1&0\\[1.1ex] 0&2\end{pmatrix}$

N’oubliez pas que les valeurs propres doivent être placées dans le même ordre que les vecteurs propres sont placés dans la matrice

$P$ .

En conclusion, la matrice de changement de base et la matrice diagonalisée sont :

$\displaystyle P = \begin{pmatrix}-1&-4 \\[1.1ex] 1&1\end{pmatrix} \qquad D= \begin{pmatrix}-1&0\\[1.1ex] 0&2\end{pmatrix}$

Exercice 3

Diagonalisez la matrice carrée suivante de dimension 3×3 :

$\displaystyle A= \begin{pmatrix}2&0&2\\[1.1ex] -1&2&1\\[1.1ex] 0&1&4\end{pmatrix}$

Voir la solution

La première étape consiste à trouver les valeurs propres de la matrice A. On calcule donc l’équation caractéristique en résolvant le déterminant de la matrice suivante :

$\displaystyle \text{det}(A-\lambda I)= \begin{vmatrix}2-\lambda&0&2\\[1.1ex] -1&2-\lambda&1\\[1.1ex] 0&1&4-\lambda \end{vmatrix} = -\lambda^3+8\lambda^2-19\lambda+12$

Il faut maintenant calculer les racines du polynôme caractéristique. Puisqu’il s’agit d’un polynôme du troisième degré, nous appliquons la règle de Ruffini :

$\displaystyle \begin{array}{r|rrrr} & -1&8&-19& 12 \\[2ex] 1 & & -1&7&-12 \\ \hline &-1\vphantom{\Bigl)}&7&-12&0 \end{array}$

Et puis on trouve les racines du polynôme obtenu :

$\displaystyle -\lambda^2+7\lambda -12=0 \ \longrightarrow \ \begin{cases} \lambda = 3 \\[2ex] \lambda = 4 \end{cases}$

Ainsi les valeurs propres de la matrice sont :

$\lambda=1 \qquad \lambda =3 \qquad \lambda = 4$

Une fois les valeurs propres trouvées, on calcule le vecteur propre associé à chacune d’elles. Tout d’abord, le vecteur propre correspondant à la valeur propre 1 :

$\displaystyle (A-I)v=0$

$\displaystyle \begin{pmatrix}1&0&2\\[1.1ex] -1&1&1\\[1.1ex] 0&1&3\end{pmatrix}\begin{pmatrix}x \\[1.1ex] y \\[1.1ex] z \end{pmatrix} =\begin{pmatrix}0 \\[1.1ex] 0 \\[1.1ex] 0\end{pmatrix}$

$\displaystyle \left.\begin{array}{l} x+2z = 0 \\[2ex] -x+y+z = 0\\[2ex] y+3z = 0\end{array}\right\} \longrightarrow \ \begin{array}{l}x=-2z \\[2ex] y = -3z \end{array}$

$\displaystyle v = \begin{pmatrix}-2 \\[1.1ex] -3 \\[1.1ex] 1\end{pmatrix}$

Puis on calcule le vecteur propre associé à la valeur propre 3 :

$\displaystyle (A-3I)v=0$

$\displaystyle \begin{pmatrix}-1&0&2\\[1.1ex] -1&-1&1\\[1.1ex] 0&1&1\end{pmatrix}\begin{pmatrix}x \\[1.1ex] y \\[1.1ex] z \end{pmatrix} =\begin{pmatrix}0 \\[1.1ex] 0 \\[1.1ex] 0\end{pmatrix}$

$\displaystyle \left.\begin{array}{l} -x+2z = 0 \\[2ex] -x-y+z = 0\\[2ex] y+z = 0\end{array}\right\} \longrightarrow \ \begin{array}{l}x=2z \\[2ex] y = -z \end{array}$

$\displaystyle v = \begin{pmatrix}2 \\[1.1ex] -1 \\[1.1ex] 1\end{pmatrix}$

Et enfin, on calcule le vecteur propre associé à la valeur propre 4 :

$\displaystyle (A-4I)v=0$

$\displaystyle \begin{pmatrix}-2&0&2\\[1.1ex] -1&-2&1\\[1.1ex] 0&1&0\end{pmatrix}\begin{pmatrix}x \\[1.1ex] y \\[1.1ex] z \end{pmatrix} =\begin{pmatrix}0 \\[1.1ex] 0 \\[1.1ex] 0\end{pmatrix}$

$\displaystyle \left.\begin{array}{l} -2x+2z = 0 \\[2ex] -x-2y+z = 0\\[2ex] y = 0\end{array}\right\} \longrightarrow \ \begin{array}{l}x=z \\[2ex] y = 0 \end{array}$

$\displaystyle v = \begin{pmatrix}1 \\[1.1ex] 0 \\[1.1ex] 1\end{pmatrix}$

Nous construisons la matrice

$P$ , formé par les vecteurs propres de la matrice :

$\displaystyle P = \begin{pmatrix}-2&2&1 \\[1.1ex] -3&-1&0 \\[1.1ex] 1&1&1 \end{pmatrix}$

Puisque toutes les valeurs propres sont différentes les unes des autres, la matrice A est diagonalisable. Ainsi la matrice diagonale correspondante est celle qui possède les valeurs propres sur la diagonale principale :

$\displaystyle D= \begin{pmatrix}1&0&0\\[1.1ex] 0&3&0 \\[1.1ex] 0&0&4\end{pmatrix}$

N’oubliez pas que les valeurs propres doivent être placées dans le même ordre que les vecteurs propres sont placés dans la matrice

$P$ .

En bref, la matrice de changement de base et la matrice diagonalisée sont :

$\displaystyle P = \begin{pmatrix}-2&2&1 \\[1.1ex] -3&-1&0 \\[1.1ex] 1&1&1\end{pmatrix} \qquad D= \begin{pmatrix}1&0&0\\[1.1ex] 0&3&0 \\[1.1ex] 0&0&4\end{pmatrix}$

Exercice 4

Diagonalisez, si possible, la matrice carrée d’ordre 3 suivante :

$\displaystyle A= \begin{pmatrix}-1&3&1\\[1.1ex] 0&2&0\\[1.1ex] 3&-1&1\end{pmatrix}$

Voir la solution

La première étape consiste à trouver les valeurs propres de la matrice A. On calcule donc l’équation caractéristique en résolvant le déterminant de la matrice suivante :

$\displaystyle \text{det}(A-\lambda I)= \begin{vmatrix}-1-\lambda&3&1\\[1.1ex] 0&2-\lambda&0\\[1.1ex] 3&-1&1-\lambda \end{vmatrix} = -\lambda^3+2\lambda^2+4\lambda-8$

Il faut maintenant calculer les racines du polynôme minimum. Puisqu’il s’agit d’un polynôme du troisième degré, nous appliquons la règle de Ruffini pour le factoriser :

$\displaystyle \begin{array}{r|rrrr} & -1&2&\phantom{-}4& -8 \\[2ex] 2 & & -2&0&8 \\ \hline &-1\vphantom{\Bigl)}&0&4&0 \end{array}$

Et puis on trouve les racines du polynôme obtenu :

$\displaystyle -\lambda^2+4=0 \ \longrightarrow \ \begin{cases} \lambda = +2 \\[2ex] \lambda = -2 \end{cases}$

Ainsi les valeurs propres de la matrice sont :

$\lambda=2 \qquad \lambda =2 \qquad \lambda = -2$

La valeur propre de -2 est de multiplicité algébrique simple, par contre la valeur propre de 2 est de multiplicité double.

Une fois les valeurs propres trouvées, on calcule le vecteur propre associé à chacune d’elles. Tout d’abord, le vecteur propre correspondant à la valeur propre -2 :

$\displaystyle (A+2I)v=0$

$\displaystyle \begin{pmatrix}1&3&1\\[1.1ex] 0&4&0\\[1.1ex] 3&-1&3\end{pmatrix}\begin{pmatrix}x \\[1.1ex] y \\[1.1ex] z \end{pmatrix} =\begin{pmatrix}0 \\[1.1ex] 0 \\[1.1ex] 0\end{pmatrix}$

$\displaystyle \left.\begin{array}{l} x+3y+z = 0 \\[2ex] 4y = 0\\[2ex] 3x-y+3z = 0\end{array}\right\} \longrightarrow \ \begin{array}{l}y=0 \\[2ex] x = -z \end{array}$

$\displaystyle v = \begin{pmatrix}1 \\[1.1ex] 0 \\[1.1ex] -1\end{pmatrix}$

Calculons maintenant les vecteurs propres associés aux valeurs propres 2.

$\displaystyle (A-2I)v=0$

$\displaystyle \begin{pmatrix}-3&3&1\\[1.1ex] 0&0&0\\[1.1ex] 3&-1&-1\end{pmatrix}\begin{pmatrix}x \\[1.1ex] y \\[1.1ex] z \end{pmatrix} =\begin{pmatrix}0 \\[1.1ex] 0 \\[1.1ex] 0\end{pmatrix}$

$\displaystyle \left.\begin{array}{l} -3x+3y+z = 0 \\[2ex] 0= 0\\[2ex] 3x-y-z = 0\end{array}\right\} \longrightarrow \ \begin{array}{l}y=0 \\[2ex] z=3x \end{array}$

$\displaystyle v = \begin{pmatrix}1 \\[1.1ex] 0 \\[1.1ex] 3\end{pmatrix}$

Puisque la valeur propre 2 est répétée deux fois, nous devons calculer un autre vecteur propre qui satisfait les équations du sous-espace (ou espace propre) :

$\displaystyle v = \begin{pmatrix}-1 \\[1.1ex] 0 \\[1.1ex] -3\end{pmatrix}$

Nous construisons la matrice

$P$ , formé par les trois vecteurs propres de la matrice :

$\displaystyle P = \begin{pmatrix}1&1&-1 \\[1.1ex] 0&0&0 \\[1.1ex] -1&3&-3 \end{pmatrix}$

Cependant, les trois vecteurs ne sont pas linéairement indépendants, puisque évidemment les deux vecteurs propres de valeur propre 2 sont une combinaison linéaire l’un de l’autre. Cela peut également être démontré parce que le déterminant de la matrice

$P$ est égal à 0 (a une ligne pleine de zéros) :

$\displaystyle \text{det}(P) = \begin{vmatrix}1&1&-1 \\[1.1ex] 0&0&0 \\[1.1ex] -1&3&-3 \end{vmatrix}=0$

Par conséquent, puisque les vecteurs propres sont linéairement dépendants, la matrice A n’est pas diagonalisable .

Exercice 5

Diagonalisez si possible la matrice carrée suivante de taille 3×3 :

$\displaystyle A= \begin{pmatrix}3&0&0\\[1.1ex] 0&2&1\\[1.1ex] 0&1&2\end{pmatrix}$

Voir la solution

La première étape consiste à trouver les valeurs propres de la matrice A. On calcule donc l’équation caractéristique en résolvant le déterminant de la matrice suivante :

$\displaystyle \text{det}(A-\lambda I)= \begin{vmatrix}3-\lambda&0&0\\[1.1ex] 0&2-\lambda&1\\[1.1ex] 0&1&2-\lambda \end{vmatrix}$

Puisque la première ligne est entièrement composée de zéros sauf 3, nous en profiterons pour résoudre le déterminant de la matrice par cofacteurs (ou adjoints) :

$\displaystyle \begin{aligned} \begin{vmatrix}3-\lambda&0&0\\[1.1ex] 0&2-\lambda&1\\[1.1ex] 0&1&2-\lambda \end{vmatrix}& = (3-\lambda)\cdot \begin{vmatrix} 2-\lambda&1\\[1.1ex]1&2-\lambda \end{vmatrix} \\[3ex] & = (3-\lambda)[\lambda^2 -4\lambda +3] \end{aligned}$

Nous devons maintenant calculer les racines du polynôme caractéristique. Il vaut mieux ne pas multiplier les parenthèses car on obtiendrait alors un polynôme du troisième degré. Par contre, si les deux facteurs sont résolus séparément, il est plus facile d’obtenir les valeurs propres :

$\displaystyle (3-\lambda)[\lambda^2 -4\lambda +3]=0 \ \longrightarrow \ \begin{cases} 3-\lambda=0 \ \longrightarrow \ \lambda = 3 \\[2ex] \lambda^2 -4\lambda +3=0 \ \longrightarrow \begin{cases}\lambda = 1 \\[2ex] \lambda = 3 \end{cases} \end{cases}$

Ainsi les valeurs propres de la matrice sont :

$\lambda=1 \qquad \lambda =3 \qquad \lambda = 3$

Une fois les valeurs propres trouvées, on calcule le vecteur propre associé à chacune d’elles. Tout d’abord, le vecteur propre correspondant à la valeur propre 1 :

$\displaystyle (A-I)v=0$

$\displaystyle \begin{pmatrix}2&0&0\\[1.1ex] 0&1&1\\[1.1ex] 0&1&1\end{pmatrix}\begin{pmatrix}x \\[1.1ex] y \\[1.1ex] z \end{pmatrix} =\begin{pmatrix}0 \\[1.1ex] 0 \\[1.1ex] 0\end{pmatrix}$

$\displaystyle \left.\begin{array}{l} 2x = 0 \\[2ex] y+z = 0\\[2ex] y+z = 0\end{array}\right\} \longrightarrow \ \begin{array}{l}x=0 \\[2ex] y = -z \end{array}$

$\displaystyle v = \begin{pmatrix}0 \\[1.1ex] -1 \\[1.1ex] 1\end{pmatrix}$

Puis on calcule les vecteurs propres associés aux valeurs propres 3 :

$\displaystyle (A-3I)v=0$

$\displaystyle \begin{pmatrix}0&0&0\\[1.1ex] 0&-1&1\\[1.1ex] 0&1&-1\end{pmatrix}\begin{pmatrix}x \\[1.1ex] y \\[1.1ex] z \end{pmatrix} =\begin{pmatrix}0 \\[1.1ex] 0 \\[1.1ex] 0\end{pmatrix}$

$\displaystyle \left.\begin{array}{l} 0 = 0 \\[2ex] -y+z = 0\\[2ex] y-z = 0\end{array}\right\} \longrightarrow \ \begin{array}{l}y=z \end{array}$

$\displaystyle v = \begin{pmatrix}0 \\[1.1ex] 1 \\[1.1ex] 1\end{pmatrix}$

Puisque la valeur propre 3 est répétée deux fois, nous devons calculer un autre vecteur propre qui satisfait les équations de l’espace propre :

$\displaystyle v = \begin{pmatrix}1 \\[1.1ex] 0 \\[1.1ex] 0\end{pmatrix}$

Nous construisons la matrice

$P$ , formé par les vecteurs propres de la matrice :

$\displaystyle P = \begin{pmatrix}0&0&1 \\[1.1ex] -1&1&0 \\[1.1ex] 1&1&0 \end{pmatrix}$

Contrairement à l’exercice 4, dans ce cas nous avons pu former 3 vecteurs linéairement indépendants bien que la multiplicité algébrique de la valeur propre 3 soit double. Cela peut être vérifié en voyant que le déterminant de la matrice

$P$ donne un résultat différent de 0 :

$\displaystyle \text{det}(P) = \begin{vmatrix}0&0&1 \\[1.1ex] -1&1&0 \\[1.1ex] 1&1&0 \end{vmatrix} =-2 \neq 0$

On peut ainsi effectuer la décomposition diagonale de la matrice A. Et la matrice diagonale correspondante est celle qui a les valeurs propres sur la diagonale principale :

$\displaystyle D= \begin{pmatrix}1&0&0\\[1.1ex] 0&3&0 \\[1.1ex] 0&0&3\end{pmatrix}$

N’oubliez pas que les valeurs propres doivent être placées dans le même ordre que les vecteurs propres sont placés dans la matrice

$P$ .

En bref, la matrice de changement de base requise pour diagonaliser la matrice et sa forme diagonalisée sont :

$\displaystyle P = \begin{pmatrix}0&0&1 \\[1.1ex] -1&1&0 \\[1.1ex] 1&1&0 \end{pmatrix}\qquad D= \begin{pmatrix}1&0&0\\[1.1ex] 0&3&0 \\[1.1ex] 0&0&3\end{pmatrix}$

Exercice 6

Effectuer la diagonalisation, si possible, de la matrice suivante de dimension 4×4 :

$\displaystyle A=\begin{pmatrix}2&1&2&0\\[1.1ex] 1&-3&1&0\\[1.1ex] 0&-1&0&0\\[1.1ex] 0&0&0&5\end{pmatrix}$

Voir la solution

La première étape consiste à trouver les valeurs propres de la matrice A. On calcule donc l’équation caractéristique en résolvant le déterminant de la matrice suivante :

$\displaystyle \text{det}(A-\lambda I)= \begin{vmatrix}2-\lambda&1&2&0\\[1.1ex] 1&-3-\lambda&1&0\\[1.1ex] 0&-1&-\lambda&0\\[1.1ex] 0&0&0&5-\lambda\end{vmatrix}$

Dans ce cas, la dernière colonne du déterminant est composée uniquement de zéros sauf un élément, nous en profiterons donc pour calculer le déterminant par cofacteurs à travers cette colonne :

$\displaystyle \begin{aligned} \begin{vmatrix}2-\lambda&1&2&0\\[1.1ex] 1&-3-\lambda&1&0\\[1.1ex] 0&-1&-\lambda&0\\[1.1ex] 0&0&0&5-\lambda\end{vmatrix}& = (5-\lambda)\cdot \begin{vmatrix}2-\lambda&1&2\\[1.1ex] 1&-3-\lambda&1\\[1.1ex] 0&-1&-\lambda\end{vmatrix}\\[3ex] & = (5-\lambda)[-\lambda^3 -\lambda^2 +6\lambda] \end{aligned}$

Il faut maintenant calculer les racines du polynôme caractéristique. Il vaut mieux ne pas faire le produit des parenthèses car on obtiendrait alors un polynôme du quatrième degré. Cependant, si les deux facteurs sont résolus séparément, il est plus facile de calculer les valeurs propres :

$\displaystyle (5-\lambda)[-\lambda^3 -\lambda^2 +6\lambda]=0 \ \longrightarrow \ \begin{cases} 5-\lambda=0 \ \longrightarrow \ \lambda = 5 \\[2ex] -\lambda^3 -\lambda^2 +6\lambda =0 \ \longrightarrow \ \lambda(-\lambda^2 -\lambda +6) =0 \end{cases}$

$\displaystyle \lambda(-\lambda^2 -\lambda +6)=0 \ \longrightarrow \ \begin{cases} \lambda=0 \\[2ex] -\lambda^2 -\lambda +6=0 \ \longrightarrow \ \begin{cases} \lambda=2 \\[2ex] \lambda = -3 \end{cases}\end{cases}$

Ainsi les valeurs propres de la matrice sont :

$\lambda=0 \qquad \lambda =-3 \qquad \lambda = 2\qquad \lambda = 5$

Une fois toutes les valeurs propres trouvées, on se dirige vers les vecteurs propres. On calcule le vecteur propre associé à la valeur propre 0 :

$\displaystyle (A-0I)v=0$

$\displaystyle \begin{pmatrix} 2&1&2&0\\[1.1ex] 1&-3&1&0\\[1.1ex] 0&-1&0&0\\[1.1ex] 0&0&0&5\end{pmatrix}\begin{pmatrix}w \\[1.1ex] x \\[1.1ex] y\\[1.1ex] z \end{pmatrix} =\begin{pmatrix}0 \\[1.1ex] 0\\[1.1ex] 0 \\[1.1ex] 0\end{pmatrix}$

$\displaystyle \left.\begin{array}{l} 2w+x+2y = 0 \\[2ex] w-3x+y = 0\\[2ex] -x=0 \\[2ex] 5z=0 \end{array}\right\} \longrightarrow \ \begin{array}{l} x=0 \\[2ex] z=0 \\[2ex]w=-y \end{array}$

$\displaystyle v = \begin{pmatrix}-1 \\[1.1ex] 0 \\[1.1ex] 1 \\[1.1ex]0 \end{pmatrix}$

On calcule le vecteur propre associé à la valeur propre -3 :

$\displaystyle (A+3I)v=0$

$\displaystyle \begin{pmatrix} 5&1&2&0\\[1.1ex] 1&0&1&0\\[1.1ex] 0&-1&3&0\\[1.1ex] 0&0&0&8\end{pmatrix}\begin{pmatrix}w \\[1.1ex] x \\[1.1ex] y\\[1.1ex] z \end{pmatrix} =\begin{pmatrix}0 \\[1.1ex] 0\\[1.1ex] 0 \\[1.1ex] 0\end{pmatrix}$

$\displaystyle \left.\begin{array}{l} 5w+x+2y = 0 \\[2ex] w+y = 0\\[2ex] -x+3y=0 \\[2ex] 8z=0 \end{array}\right\} \longrightarrow \ \begin{array}{l} w=-y \\[2ex]x=3y \\[2ex] z=0 \end{array}$

$\displaystyle v = \begin{pmatrix}-1 \\[1.1ex] 3 \\[1.1ex] 1 \\[1.1ex]0 \end{pmatrix}$

On calcule le vecteur propre associé à la valeur propre 2 :

$\displaystyle (A-2I)v=0$

$\displaystyle \begin{pmatrix} 0&1&2&0\\[1.1ex] 1&-5&1&0\\[1.1ex] 0&-1&-2&0\\[1.1ex] 0&0&0&3\end{pmatrix}\begin{pmatrix}w \\[1.1ex] x \\[1.1ex] y\\[1.1ex] z \end{pmatrix} =\begin{pmatrix}0 \\[1.1ex] 0\\[1.1ex] 0 \\[1.1ex] 0\end{pmatrix}$

$\displaystyle \left.\begin{array}{l} x+2y = 0 \\[2ex] w-5x+y = 0\\[2ex] -x-2y=0 \\[2ex] 3z=0 \end{array}\right\} \longrightarrow \ \begin{array}{l} x=-2y \\[2ex] w=-11y \\[2ex] z=0 \end{array}$

$\displaystyle v = \begin{pmatrix}-11 \\[1.1ex] -2 \\[1.1ex] 1 \\[1.1ex]0 \end{pmatrix}$

On calcule le vecteur propre associé à la valeur propre 5 :

$\displaystyle (A-5I)v=0$

$\displaystyle \begin{pmatrix} -3&1&2&0\\[1.1ex] 1&-8&1&0\\[1.1ex] 0&-1&-5&0\\[1.1ex] 0&0&0&0\end{pmatrix}\begin{pmatrix}w \\[1.1ex] x \\[1.1ex] y\\[1.1ex] z \end{pmatrix} =\begin{pmatrix}0 \\[1.1ex] 0\\[1.1ex] 0 \\[1.1ex] 0\end{pmatrix}$

$\displaystyle \left.\begin{array}{l} -3w+x+2y = 0 \\[2ex] w-8x+y = 0\\[2ex] -x-5y=0 \\[2ex] 0=0 \end{array}\right\} \longrightarrow \ \begin{array}{l} w=x=y=0 \end{array}$

$\displaystyle v = \begin{pmatrix}0 \\[1.1ex] 0 \\[1.1ex] 0 \\[1.1ex]1 \end{pmatrix}$

Nous faisons la matrice

$P$ , composé des vecteurs propres de la matrice :

$\displaystyle P = \begin{pmatrix}-1&-1&-11&0 \\[1.1ex] 0&3&-2&0 \\[1.1ex] 1&1&1&0 \\[1.1ex]0&0&0&1\end{pmatrix}$

$\displaystyle D= \begin{pmatrix}0&0&0&0\\[1.1ex] 0&-3&0&0 \\[1.1ex] 0&0&2&0\\[1.1ex] 0&0&0&5\end{pmatrix}$

N’oubliez pas que les valeurs propres doivent être placées dans le même ordre que les vecteurs propres sont positionnés dans la matrice

$P$ .

En résumé, les changements de matrice de base nécessaires pour diagonaliser la matrice A et la matrice sous forme diagonale sont :

$\displaystyle P = \begin{pmatrix}-1&-1&-11&0 \\[1.1ex] 0&3&-2&0 \\[1.1ex] 1&1&1&0 \\[1.1ex]0&0&0&1\end{pmatrix} \qquad D=\begin{pmatrix}0&0&0&0\\[1.1ex] 0&-3&0&0 \\[1.1ex] 0&0&2&0\\[1.1ex] 0&0&0&5\end{pmatrix}$

Applications des matrices diagonalisables

Si vous êtes arrivé jusqu’ici, vous vous demandez probablement : à quoi sert une matrice diagonalisable ?

Eh bien, les matrices diagonalisables sont très utiles et largement utilisées en mathématiques. La raison en est qu’une matrice diagonale est pratiquement pleine de zéros et facilite donc grandement les calculs.

Un exemple clair en est les puissances des matrices diagonalisables, car leur résultat est simplifié par la formule suivante :

$\displaystyle A^k=PD^kP^{-1}$

Cette égalité peut être facilement prouvée par induction. Il suffit donc d’élever la matrice

$D$ à l’exposant. Et comme il s’agit d’une matrice diagonale, l’opération se réduit à élever chaque terme de la diagonale principale à l’exposant :

$\displaystyle D^k = diag(\lambda_1^k,\lambda_2^k, \ldots , \lambda_n^k)$

Exemple de puissance d’une matrice diagonalisable

Pour mieux comprendre, nous allons calculer la puissance d’une matrice diagonalisable à titre d’exemple :

$\displaystyle A= \begin{pmatrix}2&0\\[1.1ex] 3&1\end{pmatrix}$

La matrice de changement de base

$P$ , formé par ses vecteurs propres, et la matrice diagonalisée $D$ , composé de ses propres valeurs, sont :

$\displaystyle P = \begin{pmatrix}0&1 \\[1.1ex] 1&3 \end{pmatrix} \qquad D= \begin{pmatrix}1&0\\[1.1ex] 0&2\end{pmatrix}$

Ainsi, pour donner un exemple, la matrice A élevée à 7 équivaut à :

$\displaystyle A^7=PD^7P^{-1}$

$\displaystyle A^7=\begin{pmatrix}0&1 \\[1.1ex] 1&3\end{pmatrix}\begin{pmatrix}1&0\\[1.1ex] 0&2\end{pmatrix}^7\left.\begin{pmatrix}0&1 \\[1.1ex] 1&3 \end{pmatrix}\right.^{-1}$

Maintenant, nous inversons la matrice

$P:$

$\displaystyle A^7=\begin{pmatrix}0&1 \\[1.1ex] 1&3 \end{pmatrix}\begin{pmatrix}1&0\\[1.1ex] 0&2\end{pmatrix}^7\begin{pmatrix}-3&1 \\[1.1ex] 1&0 \end{pmatrix}$

Nous résolvons la puissance de la matrice

$D:$

$\displaystyle A^7=\begin{pmatrix}0&1 \\[1.1ex] 1&3\end{pmatrix}\begin{pmatrix}1^7&0\\[1.1ex] 0&2^7\end{pmatrix} \begin{pmatrix}-3&1 \\[1.1ex] 1&0 \end{pmatrix}$

$\displaystyle A^7=\begin{pmatrix}0&1 \\[1.1ex] 1&3 \end{pmatrix}\begin{pmatrix}1&0\\[1.1ex] 0&128\end{pmatrix} \begin{pmatrix}-3&1 \\[1.1ex] 1&0 \end{pmatrix}$

Et, enfin, on effectue les multiplications des matrices :

$\displaystyle \bm{A^7=}\begin{pmatrix}\bm{128}&\bm{0}\\[1.1ex] \bm{381}&\bm{1}\end{pmatrix}$

Comme vous l’avez vu, il est plus pratique de calculer la puissance avec une matrice diagonale que de multiplier la même matrice sept fois de suite. Imaginez alors avec des valeurs d’exposant beaucoup plus grandes.

Propriétés des matrices diagonalisables

Les caractéristiques de ce type de matrices sont :

Si la matrice $A$ est diagonalisable, toute puissance de $A$ .

Presque toutes les matrices peuvent être diagonalisées sur un environnement complexe 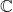$\mathbb{C}$ . Bien que ci-dessous vous ayez les exceptions qui ne sont jamais diagonalisables.

Si la matrice 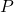$P$ est une matrice orthogonale, alors on dit que la matrice $A$ est orthogonalement diagonalisable et, par conséquent, l’équation peut être réécrite :

$\displaystyle A=PDP^t$

Une matrice est diagonalisable par une matrice unitaire si et seulement si c’est une matrice normale.

Étant donné deux matrices diagonalisables, elles sont commutables si et seulement si elles peuvent être diagonalisées simultanément, c’est-à-dire si elles partagent la même base orthonormée de vecteurs propres (ou vecteurs propres).

Si un endomorphisme est diagonalisable, on dit qu’il est diagonalisable par similarité . Cependant, tous les endomorphismes ne sont pas diagonalisables, ou en d’autres termes, la diagonalisation d’un endomorphisme n’est pas assurée.

Diagonalisation simultanée

Un ensemble de matrices est dit simultanément diagonalisable s’il existe une matrice inversible qui sert de base pour diagonaliser n’importe quelle matrice de cet ensemble. Autrement dit, si deux matrices diagonalisent sur la même base de vecteur propre, cela signifie qu’elles sont diagonalisables simultanément.

De plus, comme nous l’avons commenté dans les propriétés de la diagonalisation matricielle, si deux matrices sont capables de diagonaliser simultanément, elles doivent commuter entre elles.

Par exemple, les deux matrices suivantes sont commutables, elles diagonalisent donc sur la même base de vecteurs propres ou de vecteurs propres.

$\displaystyle A=\begin{pmatrix}2&0 \\[1.1ex] 1&-1 \end{pmatrix} \qquad B=\begin{pmatrix}3&0\\[1.1ex] 1&0 \end{pmatrix}$

Même s’ils ont les mêmes vecteurs propres, cela ne signifie pas qu’ils ont les mêmes valeurs propres. En fait, bien que les matrices A et B ci-dessus aient des vecteurs propres similaires, elles ont des valeurs propres différentes.

Matrices non diagonalisables

Bien que la grande majorité des matrices soient diagonalisables dans un environnement de nombres complexes, certaines matrices ne peuvent jamais être diagonalisées.

Ce fait se produit lorsque la multiplicité algébrique d’une valeur propre (ou valeur propre) ne coïncide pas avec la multiplicité géométrique.

Par exemple, la matrice suivante ne peut en aucun cas être diagonalisée, elle est “indiagonalisable” :

$\displaystyle \begin{pmatrix}0&1 \\[1.1ex] 0&0 \end{pmatrix}$

De plus, il existe des matrices qui ne sont pas capables de diagonaliser dans un environnement de nombres réels, mais elles diagonalisent en travaillant avec des nombres complexes, comme cette matrice :

$\displaystyle \begin{pmatrix}0&1 \\[1.1ex] -1&0 \end{pmatrix}$

Enfin, il existe certaines procédures de diagonalisation de blocs matriciels qui ne sont pas purement diagonalisables, mais qui sont un peu plus compliquées. La méthode la plus connue est la diagonalisation avec la forme canonique de Jordan .

Diagonaliser une matrice avec MATLAB

Les programmes informatiques sont très pratiques lorsqu’il s’agit de diagonaliser des matrices, surtout si elles sont très grandes. Et le logiciel le plus connu est sûrement MATLAB , nous allons donc voir ensuite comment factoriser en diagonale une matrice à l’aide de ce programme.

L’instruction utilisée pour diagonaliser une matrice avec MATLAB est :

$\displaystyle \text{[P, D] = eig(A)}$

Où

$A$ est la matrice à diagonaliser et $P$ et $D$ sont les matrices que le programme renvoie : $P$ est la matrice formée par les vecteurs propres et $D$ est la matrice sous forme diagonale dont les principaux termes diagonaux sont les valeurs propres.

Par conséquent, il vous suffit de saisir ce code dans le programme.

En revanche, si vous souhaitez uniquement connaître les valeurs propres, vous pouvez utiliser l’instruction suivante :

$\displaystyle e= eig(A)}$

Où

$e$ est le vecteur colonne que MATLAB renvoie avec les valeurs propres de la matrice $A$ .

Qu’est-ce qu’une matrice diagonalisable ?

Quand peut-on diagonaliser une matrice ?

Comment diagonaliser une matrice

Exercices de diagonalisation matricielle résolus

Exercice 1

Exercice 2

Exercice 3

Exercice 4

Exercice 5

Exercice 6

Applications des matrices diagonalisables

Exemple de puissance d’une matrice diagonalisable

Propriétés des matrices diagonalisables

Diagonalisation simultanée

Matrices non diagonalisables

Diagonaliser une matrice avec MATLAB

Leave a Comment Cancel Reply