Dans cette section, nous verrons comment discuter et résoudre un système d’équations par la méthode de Gauss-Jordan . Autrement dit, déterminez s’il s’agit d’un système compatible déterminé (SCD), d’un système compatible indéterminé (SCI) ou d’un système incompatible. De plus, vous trouverez des exemples et des exercices résolus afin que vous puissiez pratiquer et assimiler parfaitement les concepts.
Afin de comprendre ce que nous allons expliquer ensuite, il est important que vous sachiez déjà comment résoudre un système en utilisant la méthode de Gauss , nous vous recommandons donc d’y jeter un coup d’œil avant de continuer.
Systèmes compatibles déterminés par la méthode de Gauss
Tant que la dernière ligne de la matrice de Gauss est
![]() , être
, être![]() et
et![]() deux nombres quelconques, il s’agit d’un SCD (System Compatible Determined). Par conséquent, le système a une solution unique .
deux nombres quelconques, il s’agit d’un SCD (System Compatible Determined). Par conséquent, le système a une solution unique .
La grande majorité des systèmes sont SCD.
Exemple:
Par exemple, nous avons ce système :
![Rendered by QuickLaTeX.com \left. \begin{array}{r} 3x+2y-z=1 \\[2ex] 3x+8y+z=1\\[2ex] 6x+4y-z=-1 \end{array} \right\}](https://mathority.org/wp-content/ql-cache/quicklatex.com-bab5d5823e45833aa691a3510a2a23eb_l3.png)
Dont la matrice développée est :
![Rendered by QuickLaTeX.com \left. \begin{array}{r} 3x+2y-z=1 \\[2ex] 3x+8y+z=1\\[2ex] 6x+4y-z=-1 \end{array} \right\}} \ \longrightarrow \ \left( \begin{array}{ccc|c} 3 & 2 & -1 & 1 \\[2ex] 3 & 8 & 1 & 1 \\[2ex] 6 & 4 & -1 & -1 \end{array} \right)](https://mathority.org/wp-content/ql-cache/quicklatex.com-1f8daea11edeedfd6b86bb251fe19032_l3.png)
Pour résoudre le système, nous devons opérer sur les lignes de la matrice et convertir tous les éléments en dessous de la diagonale principale en 0. Ainsi, de la deuxième ligne, nous soustrayons la première ligne et de la troisième ligne, nous soustrayons la première ligne multipliée par 2 :
![Rendered by QuickLaTeX.com \left( \begin{array}{ccc|c} 3 & 2 & -1 & 1 \\[2ex] 3 & 8 & 1 & 1 \\[2ex] 6 & 4 & -1 & -1 \end{array} \right) \begin{array}{c} \\[2ex] \xrightarrow{f_2 -f_1} \\[2ex] \xrightarrow{f_3 -2f_1} & \end{array} \left( \begin{array}{ccc|c} 3 & 2 & -1 & 1 \\[2ex] 0 & 6 & 2 & 0 \\[2ex] 0 & 0 & 1 & -3 \end{array} \right)](https://mathority.org/wp-content/ql-cache/quicklatex.com-d68ac25745ddc71d1e7f55f68dd4ea7a_l3.png)
Une fois que tous les nombres en dessous de la diagonale principale sont à 0, on revient pour passer le système sous forme d’équations :
![Rendered by QuickLaTeX.com \left( \begin{array}{ccc|c} 3 & 2 & -1 & 1 \\[2ex] 0 & 6 & 2 & 0 \\[2ex] 0 & 0 & 1 & -3 \end{array} \right) \ \longrightarrow \ \left. \begin{array}{r} 3x+2y-z=1 \\[2ex] 6y+2z=0\\[2ex] 1z=-3 \end{array} \right\}](https://mathority.org/wp-content/ql-cache/quicklatex.com-4457f1b034e72c6945bfe609eff52b9a_l3.png)
Donc ce système est SCD , puisque la matrice est décalée et la dernière ligne est du type
![]() . Par conséquent, nous le résolvons comme toujours : en éliminant les inconnues des équations de bas en haut.
. Par conséquent, nous le résolvons comme toujours : en éliminant les inconnues des équations de bas en haut.
![]()
![]()
![]()
Maintenant que nous connaissons z, nous insérons sa valeur dans la deuxième équation pour trouver la valeur de
![]() :
:
![]()
![]()
![]()
![]()
![]()
Et enfin, on fait de même avec la première équation : on substitue les valeurs des autres inconnues et on résout pour
![]() :
:
![]()
![]()
![]()
![]()
![]()
![]()
La solution du système d’équations est donc :
![]()
Systèmes incompatibles par la méthode de Gauss
Lorsque dans la matrice de Gauss, nous avons une ligne avec trois 0 d’affilée et un nombre
![]() , c’est un SI (Système Incompatible), et, par conséquent, le système n’a pas de solution .
, c’est un SI (Système Incompatible), et, par conséquent, le système n’a pas de solution .
Exemple:
Par exemple, imaginons qu’après avoir opéré avec la matrice de Gauss d’un système, il nous reste :
![Rendered by QuickLaTeX.com \left( \begin{array}{ccc|c} 4 & 1 & -1 & 0 \\[2ex] 0 & 3 & 1 & -1 \\[2ex] 0 & 0 & 0 & 2 \end{array} \right)](https://mathority.org/wp-content/ql-cache/quicklatex.com-defe65fa616eff800314ebc6dc6f552b_l3.png)
Comme la dernière ligne est
![]() , c’est-à-dire trois 0 suivis d’un nombre à la fin, est un IF (Incompatible System) et, par conséquent, le système n’a pas de solution .
, c’est-à-dire trois 0 suivis d’un nombre à la fin, est un IF (Incompatible System) et, par conséquent, le système n’a pas de solution .
Bien qu’il ne soit pas nécessaire de le connaître, vous verrez ci-dessous pourquoi il n’a pas de solution.
Si nous prenons la dernière ligne, nous aurions cette équation :
![]()
Cette équation ne sera jamais remplie, car quelle que soit la valeur que prend z , la multiplier par 0 ne donnera jamais 2 (tout nombre multiplié par 0 donne toujours 0). Et puisque cette équation ne sera jamais remplie, le système n’a pas de solution.
Systèmes compatibles indéterminés par la méthode de Gauss
Chaque fois qu’une ligne de la matrice gaussienne est remplie de 0
![]() , c’est un SCI (Indeterminate Compatible System), et, par conséquent, le système a des solutions infinies .
, c’est un SCI (Indeterminate Compatible System), et, par conséquent, le système a des solutions infinies .
Voyons un exemple de la façon de résoudre un ICS :
Exemple:
![Rendered by QuickLaTeX.com \left. \begin{array}{r} x+y+2z=6 \\[2ex] 2x+3y-1z=-2 \\[2ex] 3x+4y+z=4 \end{array} \right\}](https://mathority.org/wp-content/ql-cache/quicklatex.com-18a63dfebc1f23923714e475aad2e808_l3.png)
Comme toujours, on fait d’abord la matrice développée du système :
![Rendered by QuickLaTeX.com \left. \begin{array}{r} x+y+2z=6 \\[2ex] 2x+3y-1z=-2 \\[2ex] 3x+4y+z=4 \end{array} \right\} \ \longrightarrow \ \left( \begin{array}{ccc|c} 1 & 1 & 2 & 6 \\[2ex] 2 & 3 & -1 & -2 \\[2ex] 3 & 4 & 1 & 4 \end{array} \right)](https://mathority.org/wp-content/ql-cache/quicklatex.com-f273040101827fdfea5c9a4858be5567_l3.png)
Maintenant, nous voulons que tous les nombres sous la diagonale principale soient 0. Ainsi, à la deuxième ligne, nous ajoutons la première ligne multipliée par -2 :
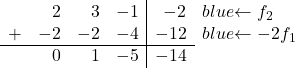
![Rendered by QuickLaTeX.com \left( \begin{array}{ccc|c} 1 & 1 & 2 & 6 \\[2ex] 2 & 3 & -1 & -2 \\[2ex] 3 & 4 & 1 & 4\end{array} \right) \begin{array}{c} \\[2ex] \xrightarrow{f_2 -2f_1} \\[2ex] & \end{array} \left( \begin{array}{ccc|c} 1 & 1 & 2 & 6 \\[2ex] 0 & 1 & -5 & -14 \\[2ex] 3 & 4 & 1 & 4 \end{array} \right)](https://mathority.org/wp-content/ql-cache/quicklatex.com-c889a6f147c6b0430731aa778121af52_l3.png)
Pour convertir 3 en 0, à la troisième ligne, nous ajoutons la première ligne multipliée par -3 :
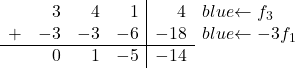
![Rendered by QuickLaTeX.com \left( \begin{array}{ccc|c} 1 & 1 & 2 & 6 \\[2ex] 0 & 1 & -5 & -14 \\[2ex] 3 & 4 & 1 & 4 \end{array} \right) \begin{array}{c} \\[2ex] \\[2ex] \xrightarrow{f_3 -3f_1} & \end{array} \left( \begin{array}{ccc|c} 1 & 1 & 2 & 6 \\[2ex] 0 & 1 & -5 & -14 \\[2ex] 0 & 1 & -5 & -14 \end{array} \right)](https://mathority.org/wp-content/ql-cache/quicklatex.com-c5acccc51108267fef6d3320068743aa_l3.png)
Pour convertir le 1 de la dernière ligne en 0, à la troisième ligne, nous ajoutons la deuxième ligne multipliée par -1 :

![Rendered by QuickLaTeX.com \left( \begin{array}{ccc|c} 1 & 1 & 2 & 6 \\[2ex] 0 & 1 & -5 & -14 \\[2ex] 0 & 1 & -5 & -14 \end{array} \right) \begin{array}{c} \\[2ex] \\[2ex] \xrightarrow{f_3 -1f_2} & \end{array} \left( \begin{array}{ccc|c} 1 & 1 & 2 & 6 \\[2ex] 0 & 1 & -5 & -14 \\[2ex] 0 & 0 & 0 & 0 \end{array} \right)](https://mathority.org/wp-content/ql-cache/quicklatex.com-a02e4819adfbe7b80d2952f87f113757_l3.png)
Puisque la dernière ligne est entièrement 0 , nous pouvons la supprimer :
![Rendered by QuickLaTeX.com \left( \begin{array}{ccc|c} 1 & 1 & 2 & 6 \\[2ex] 0 & 1 & -5 & -14 \\[2ex] 0 & 0 & 0 & 0 \end{array} \right) \ \longrightarrow \ \left( \begin{array}{ccc|c} 1 & 1 & 2 & 6 \\[2ex] 0 & 1 & -5 & -14 \end{array} \right)](https://mathority.org/wp-content/ql-cache/quicklatex.com-6aea469dceab08e6aa62571922eb2824_l3.png)
Et puisque nous avions une ligne entière remplie de 0, il s’agit d’un SCI.
On se retrouve donc avec le système suivant :
![Rendered by QuickLaTeX.com \left( \begin{array}{ccc|c} 1 & 1 & 2 & 6 \\[2ex] 0 & 1 & -5 & -14 \end{array} \right) \ \longrightarrow \ \left. \begin{array}{r} x+y+2z=6 \\[2ex] y-5z=-14 \end{array} \right\}](https://mathority.org/wp-content/ql-cache/quicklatex.com-598c031f4cba5a865952a57ed46f0f95_l3.png)
Lorsque le système est un SCI, il faut faire prendre à une inconnue la valeur du paramètre
![]() . Et nous devons résoudre le système en fonction de ce paramètre
. Et nous devons résoudre le système en fonction de ce paramètre![]() .
.
Par conséquent, nous attribuons la valeur de
![]() à z :
à z :
![]()
Bien qu’on aurait aussi pu choisir n’importe quelle autre inconnue pour prendre la valeur de
![]() .
.
Maintenant, nous isolons y de la deuxième équation et la laissons en fonction de
![]() :
:
![]()
![]()
![]()
Et enfin, nous effaçons x de la première équation et nous le laissons également en fonction de
![]() :
:
![]()
![]()
![]()
![]()
Les solutions du système sont donc :
![]()
Comme vous pouvez le voir, lorsque le système est SCI, nous laissons les solutions en fonction du paramètre
![]() . Et rappelez-vous qu’il a des solutions infinies, car selon la valeur qu’il prend
. Et rappelez-vous qu’il a des solutions infinies, car selon la valeur qu’il prend![]() , la solution sera l’une ou l’autre.
, la solution sera l’une ou l’autre.
Avant de passer aux exercices résolus, vous devez savoir que, bien que dans cet article nous utilisons la méthode de Gauss, une autre façon de discuter et de résoudre des systèmes d’équations linéaires est le théorème de Rouche . En fait, il est probablement plus utilisé.
Exercices résolus pour la discussion de systèmes d’équations par la méthode de Gauss-Jordan
Exercice 1
Déterminez quel type de système est impliqué et résolvez le système d’équations suivant en utilisant la méthode de Gauss :
![Rendered by QuickLaTeX.com \left. \begin{array}{r} x+y+2z=6 \\[2ex] 2x+3y+5z=8 \\[2ex] 3x+3y+6z=9 \end{array} \right\}](https://mathority.org/wp-content/ql-cache/quicklatex.com-be4ba1bd1ce7452e66c5189d995d948c_l3.png)
La première chose que nous devons faire est la matrice étendue du système :
![Rendered by QuickLaTeX.com \left. \begin{array}{r} x+y+2z=6 \\[2ex] 2x+3y+5z=8 \\[2ex] 3x+3y+6z=9 \end{array} \right\} \longrightarrow \left( \begin{array}{ccc|c} 1 & 1 & 2 & 6 \\[2ex] 2 & 3 & 5 & 8 \\[2ex] 3 & 3 & 6 & 9 \end{array} \right)](https://mathority.org/wp-content/ql-cache/quicklatex.com-b600f3fc0d79a06eb972dbacb673a780_l3.png)
Maintenant, nous devons faire en sorte que tous les nombres sous le tableau principal soient 0.
Nous effectuons donc des opérations de ligne pour annuler les deux derniers termes de la première colonne :
![Rendered by QuickLaTeX.com \left( \begin{array}{ccc|c} 1 & 1 & 2 & 6 \\[2ex] 2 & 3 & 5 & 8 \\[2ex]3 & 3 & 6 & 9 \end{array} \right) \begin{array}{c} \\[2ex] \xrightarrow{f_2 - 2f_1} \\[2ex] \xrightarrow{f_3 - 3f_1}& \end{array} \left( \begin{array}{ccc|c} 1 & 1 & 2 & 6 \\[2ex] 0 & 1 & 1 & -4 \\[2ex] 0 & 0 & 0 & -9 \end{array} \right)](https://mathority.org/wp-content/ql-cache/quicklatex.com-a1d832d5bb115666614ae96822c360eb_l3.png)
Nous avons obtenu une ligne de la matrice composée de trois 0 suivis d’un nombre. Il s’agit donc d’un SI (Système Incompatible) et le système n’a pas de solution.
Exercice 2
Déterminez de quel type de système il s’agit et trouvez la solution du système d’équations suivant en utilisant la méthode de Gauss :
![Rendered by QuickLaTeX.com \left. \begin{array}{r} x-2y+3z=1 \\[2ex] -2x+5y-z=5 \\[2ex] -x+3y+2z=6 \end{array} \right\}](https://mathority.org/wp-content/ql-cache/quicklatex.com-7f5aba495f2c6a301e923ee3c6238012_l3.png)
La première chose que nous devons faire est la matrice étendue du système :
![Rendered by QuickLaTeX.com \left. \begin{array}{r} x-2y+3z=1 \\[2ex] -2x+5y-z=5 \\[2ex] -x+3y+2z=6 \end{array} \right\} \longrightarrow \left( \begin{array}{ccc|c} 1 & -2 & 3 & 1 \\[2ex] -2 & 5 & -1 & 5 \\[2ex] -1 & 3 & 2 & 6 \end{array} \right)](https://mathority.org/wp-content/ql-cache/quicklatex.com-f8bb5e5ab85946bddad72067fe17d937_l3.png)
Maintenant, nous devons faire en sorte que tous les nombres sous le tableau principal soient 0.
Nous effectuons donc des opérations de ligne pour annuler les deux derniers termes de la première colonne :
![Rendered by QuickLaTeX.com \left( \begin{array}{ccc|c} 1 & -2 & 3 & 1 \\[2ex] -2 & 5 & -1 & 5 \\[2ex] -1 & 3 & 2 & 6 \end{array} \right) \begin{array}{c} \\[2ex] \xrightarrow{f_2 + 2f_1} \\[2ex] \xrightarrow{f_3 + f_1} \end{array} \left( \begin{array}{ccc|c} 1 & -2 & 3 & 1 \\[2ex] 0 & 1 & 5 & 7 \\[2ex] 0 & 1 & 5 & 7 \end{array} \right)](https://mathority.org/wp-content/ql-cache/quicklatex.com-83e48becaaa6683719ac57eb7d118943_l3.png)
Essayons maintenant de supprimer le dernier élément de la deuxième colonne :
![Rendered by QuickLaTeX.com \left( \begin{array}{ccc|c}1 & -2 & 3 & 1 \\[2ex] 0 & 1 & 5 & 7 \\[2ex] 0 & 1 & 5 & 7 \end{array} \right) \begin{array}{c} \\[2ex] \\[2ex] \xrightarrow{f_3 -f_2} \end{array} \left( \begin{array}{ccc|c} 1 & -2 & 3 & 1 \\[2ex] 0 & 1 & 5 & 7 \\[2ex] 0 & 0 & 0 & 0 \end{array} \right)](https://mathority.org/wp-content/ql-cache/quicklatex.com-16a1afc0eb224ee5f05c9e313586854d_l3.png)
Mais nous obtenons une rangée entière de 0. Il s’agit donc d’un SCI et le système a une infinité de solutions.
Mais comme il s’agit d’un SCI, on peut résoudre le système en se basant sur
![]() . Nous supprimons donc la ligne de 0 :
. Nous supprimons donc la ligne de 0 :
![Rendered by QuickLaTeX.com \left( \begin{array}{ccc|c} 1 & -2 & 3 & 1 \\[2ex] 0 & 1 & 5 & 7 \\[2ex] 0 & 0 & 0 & 0 \end{array} \right) \ \longrightarrow \ \left( \begin{array}{ccc|c} 1 & -2 & 3 & 1 \\[2ex] 0 & 1 & 5 & 7 \end{array} \right)](https://mathority.org/wp-content/ql-cache/quicklatex.com-5c838c5f1b229d4c8a43ac9ddd8e3629_l3.png)
On exprime maintenant la matrice sous la forme d’un système d’équations à inconnues :
![Rendered by QuickLaTeX.com \left( \begin{array}{ccc|c} 1 & -2 & 3 & 1 \\[2ex] 0 & 1 & 5 & 7 \end{array} \right) \ \longrightarrow \ \left. \begin{array}{r} 1x-2y+3z=1 \\[2ex] 1y+5z=7 \end{array} \right\}](https://mathority.org/wp-content/ql-cache/quicklatex.com-b3fd941d33fec646d16b8181430c9986_l3.png)
Nous donnons la valeur de
![]() pour
pour ![]()
![]()
Nous remplaçons la valeur de
![]() dans la deuxième équation pour trouver la valeur de
dans la deuxième équation pour trouver la valeur de ![]()
![]()
![]()
![]()
Et on fait de même avec la première équation : on substitue les valeurs des autres inconnues et on efface
![]()
![]()
![]()
![]()
![]()
La solution du système d’équations est donc :
![]()
Exercice 3
Trouvez de quel type de système il s’agit et résolvez le système d’équations suivant par la méthode de Gauss :
![Rendered by QuickLaTeX.com \left. \begin{array}{r} 4x-4y+z=-4 \\[2ex] x+3y+z=2 \\[2ex] x+5y+2z=6 \end{array} \right\}](https://mathority.org/wp-content/ql-cache/quicklatex.com-b04370b42854e53c650ca0eae14aadb5_l3.png)
La première chose que nous devons faire est la matrice étendue du système :
![Rendered by QuickLaTeX.com \left. \begin{array}{r} 4x-4y+z=-4 \\[2ex] x+3y+z=2 \\[2ex] x+5y+2z=6\end{array} \right\} \longrightarrow \left( \begin{array}{ccc|c} 4 & -4 & 1 & -4 \\[2ex] 1 & 3 & 1 & 2 \\[2ex] 1 & 5 & 2 & 6 \end{array} \right)](https://mathority.org/wp-content/ql-cache/quicklatex.com-ff2c7644e19fdf405f3c5c42ffc0ee98_l3.png)
Pour appliquer la méthode de Gauss, c’est plus simple si le premier nombre de la première ligne est un 1. Nous allons donc changer l’ordre des lignes 1 et 2 :
![Rendered by QuickLaTeX.com \left( \begin{array}{ccc|c} 4 & -4 & 1 & -4 \\[2ex] 1 & 3 & 1 & 2 \\[2ex] 1 & 5 & 2 & 6 \end{array} \right) \begin{array}{c} \xrightarrow{f_1 \rightarrow f_2} \\[2ex] \xrightarrow{f_2 \rightarrow f_1} \\[2ex] & \end{array} \left( \begin{array}{ccc|c} 1 & 3 & 1 & 2 \\[2ex] 4 & -4 & 1 & -4 \\[2ex] 1 & 5 & 2 & 6 \end{array} \right)](https://mathority.org/wp-content/ql-cache/quicklatex.com-471d89605d4bf6ddef1896a8fbe4c5ea_l3.png)
Maintenant, nous devons faire en sorte que tous les nombres sous le tableau principal soient 0.
Nous effectuons donc des opérations de ligne pour annuler les deux derniers termes de la première colonne :
![Rendered by QuickLaTeX.com \left( \begin{array}{ccc|c} 1 & 3 & 1 & 2 \\[2ex] 4 & -4 & 1 & -4 \\[2ex] 1 & 5 & 2 & 6 \end{array} \right) \begin{array}{c} \\[2ex] \xrightarrow{f_2 - 4f_1} \\[2ex] \xrightarrow{f_3 -f_1} \end{array} \left( \begin{array}{ccc|c} 1 & 3 & 1 & 2 \\[2ex] 0 & -16 & -3 & -12 \\[2ex] 0 & 2 & 1 & 4 \end{array} \right)](https://mathority.org/wp-content/ql-cache/quicklatex.com-f4d5cbc50b87927077018175c4678e90_l3.png)
Maintenant, nous convertissons le dernier élément de la deuxième colonne en zéro :
![Rendered by QuickLaTeX.com \left( \begin{array}{ccc|c}1 & 3 & 1 & 2 \\[2ex] 0 & -16 & -3 & -12 \\[2ex] 0 & 2 & 1 & 4 \end{array} \right) \begin{array}{c} \\[2ex] \\[2ex] \xrightarrow{8f_3 + f_2} \end{array} \left( \begin{array}{ccc|c}1 & 3 & 1 & 2 \\[2ex] 0 & -16 & -3 & -12 \\[2ex] 0 & 0 & 5 & 20 \end{array} \right)](https://mathority.org/wp-content/ql-cache/quicklatex.com-9013720883fd719e2bd0779bfbaa7a9f_l3.png)
Ce système est SCD , puisque nous avons réussi à avoir la matrice décalée et la dernière ligne est du type
![]() . Par conséquent, il aura une solution unique.
. Par conséquent, il aura une solution unique.
Une fois que tous les nombres sous la diagonale principale sont 0, nous pouvons maintenant résoudre le système d’équations. Pour ce faire, on exprime à nouveau la matrice sous la forme d’un système d’équations à inconnues :
![Rendered by QuickLaTeX.com \left( \begin{array}{ccc|c} 1 & 3 & 1 & 2 \\[2ex] 0 & -16 & -3 & -12 \\[2ex] 0 & 0 & 5 & 20 \end{array} \right) \ \longrightarrow \ \left. \begin{array}{r} x+3y+1z=2 \\[2ex] -16y-3z=-12 \\[2ex] 5z=20 \end{array} \right\}](https://mathority.org/wp-content/ql-cache/quicklatex.com-0f0433738d5d0a22bdd3b04dbd44fd1e_l3.png)
Et on résout les inconnues des équations de bas en haut. On résout d’abord la dernière équation :
![]()
![]()
Maintenant, nous substituons la valeur de z dans la deuxième équation pour trouver la valeur de y :
![]()
![]()
![]()
![]()
![]()
Et on fait de même avec la première équation : on substitue les valeurs des autres inconnues et on résout pour x :
![]()
![]()
![]()
![]()
La solution du système d’équations est donc :
![]()
Exercice 4
Déterminez de quel type de système il s’agit et résolvez le système d’équations suivant par la méthode de Gauss :
![Rendered by QuickLaTeX.com \left. \begin{array}{r} x-y+4z=2 \\[2ex] -3x-3y+3z=7 \\[2ex] -2x-4y+7z=9 \end{array} \right\}](https://mathority.org/wp-content/ql-cache/quicklatex.com-4e8a133547b4719d7833a792550fd322_l3.png)
La première chose que nous devons faire est la matrice étendue du système :
![Rendered by QuickLaTeX.com \left. \begin{array}{r} x-y+4z=2 \\[2ex] -3x-3y+3z=7 \\[2ex] -2x-4y+7z=9 \end{array} \right\} \longrightarrow \left( \begin{array}{ccc|c}1 & -1 & 4 & 2 \\[2ex] -3 & -3 & 3 & 7 \\[2ex] -2 & -4 & 7 & 9\end{array} \right)](https://mathority.org/wp-content/ql-cache/quicklatex.com-cc41f78456a922a0fbff419d336b0b46_l3.png)
Maintenant, nous devons faire en sorte que tous les nombres sous le tableau principal soient 0.
Nous effectuons donc des opérations de ligne pour annuler les deux derniers termes de la première colonne :
![Rendered by QuickLaTeX.com \left( \begin{array}{ccc|c} 1 & -1 & 4 & 2 \\[2ex] -3 & -3 & 3 & 7 \\[2ex] -2 & -4 & 7 & 9\end{array} \right) \begin{array}{c} \\[2ex] \xrightarrow{f_2 + 3f_1} \\[2ex] \xrightarrow{f_3 + 2f_1} \end{array} \left( \begin{array}{ccc|c} 1 & -1 & 4 & 2 \\[2ex] 0 & -6 & 15 & 13\\[2ex] 0 & -6 & 15 & 13\end{array} \right)](https://mathority.org/wp-content/ql-cache/quicklatex.com-ff92912f653c6aca7ceb7c990c9635a3_l3.png)
Essayons maintenant de supprimer le dernier élément de la deuxième colonne :
![Rendered by QuickLaTeX.com \left( \begin{array}{ccc|c}1 & -1 & 4 & 2 \\[2ex] 0 & -6 & 15 & 13\\[2ex] 0 & -6 & 15 & 13\end{array} \right) \begin{array}{c} \\[2ex] \\[2ex] \xrightarrow{f_3 -1f_2} \end{array} \left( \begin{array}{ccc|c} 1 & -1 & 4 & 2 \\[2ex] 0 & -6 & 15 & 13\\[2ex] 0 & 0 & 0 & 0 \end{array} \right)](https://mathority.org/wp-content/ql-cache/quicklatex.com-3c6904a64a721f3a92bef8c6b7d713cf_l3.png)
Mais nous obtenons une rangée entière de 0. Il s’agit donc d’un SCI et le système a une infinité de solutions.
Mais comme il s’agit d’un SCI, on peut résoudre le système en se basant sur
![]() . Nous supprimons donc la ligne de 0 :
. Nous supprimons donc la ligne de 0 :
![Rendered by QuickLaTeX.com \left( \begin{array}{ccc|c} 1 & -1 & 4 & 2 \\[2ex] 0 & -6 & 15 & 13\\[2ex] 0 & 0 & 0 & 0 \end{array} \right) \ \longrightarrow \ \left( \begin{array}{ccc|c} 1 & -1 & 4 & 2 \\[2ex] 0 & -6 & 15 & 13 \end{array} \right)](https://mathority.org/wp-content/ql-cache/quicklatex.com-6d856e2c1246f3629d68a7bcd3cd759a_l3.png)
On exprime maintenant la matrice sous la forme d’un système d’équations à inconnues :
![Rendered by QuickLaTeX.com \left( \begin{array}{ccc|c} 1 & -1 & 4 & 2 \\[2ex] 0 & -6 & 15 & 13 \end{array} \right) \ \longrightarrow \ \left. \begin{array}{r} 1x-1y+4z=2 \\[2ex] -6y+15z=13 \end{array} \right\}](https://mathority.org/wp-content/ql-cache/quicklatex.com-a4cf1265bfc12f94580de183230c8b7c_l3.png)
Nous donnons la valeur de
![]() pour
pour ![]()
![]()
Nous remplaçons la valeur de
![]() dans la deuxième équation pour trouver la valeur de
dans la deuxième équation pour trouver la valeur de ![]()
![]()
![]()
![]()
![]()
Et on fait de même avec la première équation : on substitue les valeurs des autres inconnues et on efface
![]()
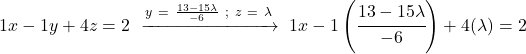
![]()
![]()
Nous avons une somme avec des fractions. Par conséquent, nous réduisons tous les termes à un dénominateur commun :
![]()
![]()
Puisqu’ils ont maintenant tous le même dénominateur, nous pouvons les regrouper en une seule fraction :
![]()
Et enfin on opère sur le numérateur :
![]()
![]()
La solution du système d’équations est donc :
![]()