Sur cette page nous allons découvrir ce qu’est le théorème de Rouché Frobenius et comment calculer le rang d’une matrice avec lui. Vous trouverez également des exemples et des exercices résolus pas à pas avec le théorème de Rouché-Frobenius.
Qu’est-ce que le théorème de Rouché-Frobenius ?
Le théorème de Rouché-Frobenius est une méthode qui permet de classer les systèmes d’équations linéaires. Autrement dit, le théorème de Rouché-Frobenius est utilisé pour savoir combien de solutions un système d’équations a sans avoir à le résoudre.
Il existe 3 types de systèmes d’équations :
- Système compatible déterminé (SCD) : le système a une solution unique.
- Système compatible indéterminé (SCI) : le système a une infinité de solutions.
- Système incompatible (SI) : le système n’a pas de solution.
De plus, le théorème de Rouché-Frobenius nous permettra aussi plus tard de résoudre des systèmes par la règle de Cramer .
Énoncé du théorème de Rouché-Frobenius
Le théorème de Rouché-Frobenius dit que
est la matrice formée par les coefficients des inconnues d’un système d’équations. et le ventre
, ou matrice étendue , est la matrice formée par les coefficients des inconnues d’un système d’équations et les termes indépendants :
Le théorème de Rouché-Frobenius permet de savoir à quel type de système d’équations on a affaire selon le rang des matrices A et A’ :
- Si rang(A) = rang(A’) = nombre d’inconnues ⟶ Système compatible déterminé (SCD)
- Si rang(A) = rang(A’) < nombre d’inconnues ⟶ Système compatible indéterminé (SCI)
- si gamme(A)
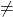plage (A’) ⟶ Système incompatible (SI)
Une fois que nous savons ce que dit le théorème de Rouché-Frobenius, nous allons voir comment résoudre les exercices du théorème de Rouché-Frobenius. Voici donc 3 exemples : un exercice résolu à l’aide du théorème de chaque type de système d’équations.
Exemple de système compatible déterminé (SCD)
![\begin{cases} 2x+y-3z=0 \\[1.5ex] x+2y-z= 1 \\[1.5ex] 4x-2y+z = 3\end{cases}](https://mathority.org/wp-content/ql-cache/quicklatex.com-b6b2f93c6308c25e8df2fbb5da2af9a8_l3.png "Rendered by QuickLaTeX.com")
La matrice A et la matrice étendue A’ du système sont :
![\displaystyle A= \left( \begin{array}{ccc} 2 & 1 & -3 \\[1.1ex] 1 & 2 & -1 \\[1.1ex] 4 & -2 & 1 \end{array} \right) \qquad A'= \left( \begin{array}{ccc|c} 2 & 1 & -3 & 0 \\[1.1ex] 1 & 2 & -1 & 1 \\[1.1ex] 4 & -2 & 1 & 3\end{array} \right)](https://mathority.org/wp-content/ql-cache/quicklatex.com-4597f5171b586bbcf0915d8512f7b89d_l3.png "Rendered by QuickLaTeX.com")
On calcule maintenant le rang de la matrice A. Pour ce faire, on vérifie si le déterminant de toute la matrice est différent de 0 :
![\displaystyle \begin{vmatrix}A \end{vmatrix}= \begin{vmatrix} 2 & 1 & -3 \\[1.1ex] 1 & 2 & -1 \\[1.1ex] 4 & -2 & 1 \end{vmatrix} = 25 \neq 0](https://mathority.org/wp-content/ql-cache/quicklatex.com-6c95b7158a2e6401cd16aeb708f128ff_l3.png "Rendered by QuickLaTeX.com")
Comme la matrice a un déterminant 3×3 différent de 0, la matrice A est de rang 3 :
Une fois qu’on connaît le rang de A, on calcule le rang de A’, qui sera au moins de rang 3 car on vient de voir qu’il a à l’intérieur un déterminant d’ordre 3 différent de 0. De plus, il ne peut pas être de rang 4, puisqu’on ne peut faire aucun déterminant d’ordre 4. Donc, la matrice A’ est aussi de rang 3 :
Ainsi, puisque le rang de la matrice A est égal au rang de la matrice A’ et au nombre d’inconnues du système (3), on sait par le théorème de Rouché Frobenius qu’il s’agit d’un Système Déterminé Compatible (SCD) :
![\displaystyle \begin{array}{c} \begin{array}{c} \color{black}rg(A) = 3 \\[1.3ex] \color{black}rg(A')=3 \\[1.3ex] \color{black}\text{N\'umero de inc\'ognitas} = 3 \end{array}} \\ \\ \color{blue} \boxed{ \color{black}\phantom{^9_9} rg(A) = rg(A') = n = 3 \color{blue} \ \bm{\longrightarrow} \ \color{black} \bm{SCD}\phantom{^9_9}} \end{array}](https://mathority.org/wp-content/ql-cache/quicklatex.com-557185e16670c72d23eec5a3ea13b487_l3.png "Rendered by QuickLaTeX.com")
Exemple de système compatible indéterminé (ICS)
![\begin{cases} x-y+2z=1 \\[1.5ex] 3x+2y+z= 5 \\[1.5ex] 2x+3y-z = 4\end{cases}](https://mathority.org/wp-content/ql-cache/quicklatex.com-2360b9a47257f73cf3f5dea63fb24098_l3.png "Rendered by QuickLaTeX.com")
La matrice A et la matrice étendue A’ du système sont :
![\displaystyle A= \left( \begin{array}{ccc} 1 & -1 & 2 \\[1.1ex] 3 & 2 & 1 \\[1.1ex] 2 & 3 & -1 \end{array} \right) \qquad A'= \left( \begin{array}{ccc|c} 1 & -1 & 2 & 1 \\[1.1ex] 3 & 2 & 1 & 5 \\[1.1ex] 2 & 3 & -1 & 4 \end{array} \right)](https://mathority.org/wp-content/ql-cache/quicklatex.com-b281235e2702433b447e2586ae3092c9_l3.png "Rendered by QuickLaTeX.com")
On calcule maintenant le rang de la matrice A. Pour ce faire, on vérifie si le déterminant de toute la matrice est différent de 0 :
![\displaystyle \begin{vmatrix}A \end{vmatrix}= \begin{vmatrix} 1 & -1 & 2 \\[1.1ex] 3 & 2 & 1 \\[1.1ex] 2 & 3 & -1 \end{vmatrix} = 0](https://mathority.org/wp-content/ql-cache/quicklatex.com-74cafc27ab41134696c3bf263132b98b_l3.png "Rendered by QuickLaTeX.com")
Le déterminant de toute la matrice A donne 0, donc elle n’est pas de rang 3. Pour voir si elle est de rang 2, il faut trouver une sous-matrice dans A dont le déterminant est différent de 0. Par exemple, celle du haut coin gauche :
![\displaystyle \begin{vmatrix} 1 & -1 \\[1.1ex] 3 & 2 \end{vmatrix} = 5 \neq 0](https://mathority.org/wp-content/ql-cache/quicklatex.com-22b2487f7664a70c116593120de2743b_l3.png "Rendered by QuickLaTeX.com")
Comme la matrice a un déterminant 2×2 différent de 0, la matrice A est de rang 2 :
Une fois que nous connaissons le rang de A, nous calculons le rang de A’. On sait déjà que le déterminant des 3 premières colonnes donne 0, on essaie donc les autres déterminants 3×3 possibles :
![\displaystyle \begin{vmatrix}1 & -1 & 1 \\[1.1ex] 3 & 2 & 5 \\[1.1ex] 2 & 3 & 4\end{vmatrix} = 0 \quad \begin{vmatrix}1 & 2 & 1 \\[1.1ex] 3 & 1 & 5 \\[1.1ex] 2 & -1 & 4\end{vmatrix} = 0 \quad \begin{vmatrix} -1 & 2 & 1 \\[1.1ex] 2 & 1 & 5 \\[1.1ex] 3 & -1 & 4\end{vmatrix} = 0](https://mathority.org/wp-content/ql-cache/quicklatex.com-17f264ad3859da88ffa6784be24e4143_l3.png "Rendered by QuickLaTeX.com")
Tous les déterminants 3×3 de la matrice A’ sont 0, donc la matrice A’ ne sera pas non plus de rang 3. Cependant, à l’intérieur elle a bien des déterminants d’ordre 2 différents de 0. Par exemple :
Donc la matrice A’ sera de rang 2 :
L’étendue de la matrice A est égale à l’étendue de la matrice A’ mais celles-ci sont inférieures au nombre d’inconnues du système (3). Par conséquent, selon le théorème de Rouché-Frobenius, il s’agit d’un système compatible indéterminé (SCI) :
![\displaystyle \begin{array}{c} \begin{array}{c} \color{black}rg(A) = 2 \\[1.3ex] \color{black}rg(A')=2 \\[1.3ex] \color{black}\text{N\'umero de inc\'ognitas} = 3 \end{array}} \\ \\ \color{blue} \boxed{ \color{black}\phantom{^9_9} rg(A) = rg(A') = 2 \ < \ n =3 \color{blue} \ \bm{\longrightarrow} \ \color{black} \bm{SCI}\phantom{^9_9}} \end{array}](https://mathority.org/wp-content/ql-cache/quicklatex.com-96868a2569ea0ab5ca99d8dc606d3dc9_l3.png "Rendered by QuickLaTeX.com")
Exemple de système incompatible (SI)
![\begin{cases} 2x+y-2z=3 \\[1.5ex] 3x-2y+z= 2 \\[1.5ex] x+4-5z = 3 \end{cases}](https://mathority.org/wp-content/ql-cache/quicklatex.com-30e1084dd637eb4371f6b2218af24136_l3.png "Rendered by QuickLaTeX.com")
La matrice A et la matrice étendue A’ du système sont :
![\displaystyle A= \left( \begin{array}{ccc} 2 & 1 & -2 \\[1.1ex] 3 & -2 & 1 \\[1.1ex] 1 & 4 & -5 \end{array} \right) \qquad A'= \left( \begin{array}{ccc|c} 2 & 1 & -2 & 3 \\[1.1ex] 3 & -2 & 1 & 2 \\[1.1ex] 1 & 4 & -5 & 3 \end{array} \right)](https://mathority.org/wp-content/ql-cache/quicklatex.com-b435d86f1466af5748d91e6c9bd813e3_l3.png "Rendered by QuickLaTeX.com")
On calcule maintenant le rang de la matrice A. Pour ce faire, on vérifie si le déterminant de toute la matrice est différent de 0 :
![\displaystyle \begin{vmatrix}A \end{vmatrix}= \begin{vmatrix} 2 & 1 & -2 \\[1.1ex] 3 & -2 & 1 \\[1.1ex] 1 & 4 & -5 \end{vmatrix} = 0](https://mathority.org/wp-content/ql-cache/quicklatex.com-714538c91aa2620a6adb40581245f0e0_l3.png "Rendered by QuickLaTeX.com")
Le déterminant de toute la matrice A donne 0, donc elle n’est pas de rang 3. Pour voir si elle est de rang 2, il faut trouver une sous-matrice dans A dont le déterminant est différent de 0. Par exemple, celle du haut coin gauche :
![\displaystyle \begin{vmatrix} 2 & 1 \\[1.1ex] 3 & -2 \end{vmatrix} = -7 \neq 0](https://mathority.org/wp-content/ql-cache/quicklatex.com-5a46decda8fd850d9c847922b0c896db_l3.png "Rendered by QuickLaTeX.com")
Comme la matrice a un déterminant d’ordre 2 différent de 0, la matrice A est de rang 2 :
Une fois que nous connaissons le rang de A, nous calculons le rang de A’. On sait déjà que le déterminant des 3 premières colonnes donne 0, alors maintenant on essaie, par exemple, avec le déterminant des 3 dernières colonnes :
![\displaystyle \begin{vmatrix} 1 & -2 & 3 \\[1.1ex] -2 & 1 & 2 \\[1.1ex] 4 & -5 & 3 \end{vmatrix} = 3 \neq 0](https://mathority.org/wp-content/ql-cache/quicklatex.com-47aecdf801b92f21f2287fb96eaaa3f8_l3.png "Rendered by QuickLaTeX.com")
Par contre, la matrice A’ contient bien un déterminant dont le résultat est différent de 0, donc la matrice A’ aura le rang 3 :
Donc, puisque le rang de la matrice A est plus petit que le rang de la matrice A’, on déduit du théorème de Rouché-Frobenius qu’il s’agit d’un Système Incompatible (SI) :
![\displaystyle \begin{array}{c} \begin{array}{c} \color{black}rg(A) = 2 \\[1.3ex] \color{black}rg(A')=3 \\[1.3ex] \color{black}\text{N\'umero de inc\'ognitas} = 3 \end{array}} \\ \\ \color{blue} \boxed{ \color{black}\phantom{^9_9} rg(A) = 2 \ \neq \ rg(A') = 3 \color{blue} \ \bm{\longrightarrow} \ \color{black} \bm{SI}\phantom{^9_9}} \end{array}](https://mathority.org/wp-content/ql-cache/quicklatex.com-c3da0513f318d25473e93ba88c51fb42_l3.png "Rendered by QuickLaTeX.com")
Problèmes résolus du théorème de Rouché – Frobenius
Exercice 1
Déterminer le type du système d’équations à 3 inconnues suivant à l’aide du théorème de Rouché-Frobenius :
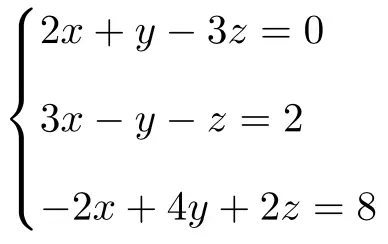
On fait d’abord la matrice A et la matrice étendue A’ du système :
![\displaystyle A= \left( \begin{array}{ccc} 2 & 1 & -3 \\[1.1ex] 3 & -1 & -1 \\[1.1ex] -2 & 4 & 2 \end{array} \right) \qquad A'= \left( \begin{array}{ccc|c} 2 & 1 & -3 & 0 \\[1.1ex] 3 & -1 & -1 & 2 \\[1.1ex] -2 & 4 & 2 & 8 \end{array} \right)](https://mathority.org/wp-content/ql-cache/quicklatex.com-951ce5c1f0c606d4f060a1de58b60303_l3.png "Rendered by QuickLaTeX.com")
Il faut maintenant trouver le rang de la matrice A. Pour cela, on vérifie si le déterminant de la matrice est différent de 0 :
![\displaystyle \begin{vmatrix}A \end{vmatrix}= \begin{vmatrix} 2 & 1 & -3 \\[1.1ex] 3 & -1 & -1 \\[1.1ex] -2 & 4 & 2 \end{vmatrix} = -4+2-36+6+8-6=-30 \bm{\neq 0}](https://mathority.org/wp-content/ql-cache/quicklatex.com-15cddb69f7590648d1d6ae61d942471e_l3.png "Rendered by QuickLaTeX.com")
La matrice ayant un déterminant de troisième ordre différent de 0, la matrice A est de rang 3 :
Une fois que nous connaissons le rang de A, nous calculons le rang de A’. Celui-ci sera au moins de rang 3, car nous venons de voir qu’il a à l’intérieur un déterminant d’ordre 3 différent de 0. De plus, il ne peut pas être de rang 4, puisqu’on ne peut pas faire de déterminant 4×4. Donc, la matrice A’ est aussi de rang 3 :
Ainsi, grâce au théorème de Rouché-Frobenius, nous savons qu’il s’agit d’un système compatible déterminé (SCD), car la plage de A est égale à la plage de A’ et au nombre d’inconnues.
![\displaystyle \begin{array}{c} \begin{array}{c} \color{black}rg(A) = 3 \\[1.3ex] \color{black}rg(A')=3 \\[1.3ex] \color{black}\text{N\'umero de inc\'ognitas} = 3 \end{array}} \\ \\ \color{blue} \boxed{ \color{black}\phantom{^9_9} rg(A) = rg(A') = n = 3 \color{blue} \ \bm{\longrightarrow} \ \color{black} \bm{SCD}\phantom{^9_9}} \end{array}](https://mathority.org/wp-content/ql-cache/quicklatex.com-31b495a48a75d7af1f23e38818bf4eca_l3.png "Rendered by QuickLaTeX.com")
Exercice 2
Classer le système d’équations à 3 inconnues suivant à l’aide du théorème de Rouché-Frobenius :
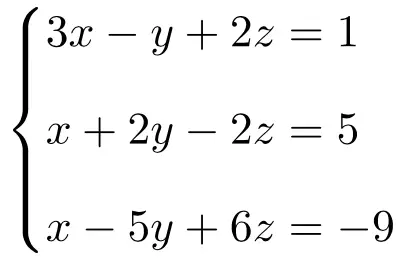
On construit tout d’abord la matrice A et la matrice étendue A’ du système :
![\displaystyle A= \left( \begin{array}{ccc}3 & -1 & 2 \\[1.1ex] 1 & 2 & -2 \\[1.1ex] 1 & -5 & 6 \end{array} \right) \qquad A'= \left( \begin{array}{ccc|c} 3 & -1 & 2 & 1 \\[1.1ex] 1 & 2 & -2 & 5 \\[1.1ex] 1 & -5 & 6 & -9 \end{array} \right)](https://mathority.org/wp-content/ql-cache/quicklatex.com-45e13aabe233ece927df7c9ba0bb3ec1_l3.png "Rendered by QuickLaTeX.com")
Calculons maintenant la plage de la matrice A :
![\displaystyle \begin{vmatrix}A \end{vmatrix}= \begin{vmatrix} 3 & -1 & 2 \\[1.1ex] 1 & 2 & -2 \\[1.1ex] 1 & -5 & 6 \end{vmatrix} = 0](https://mathority.org/wp-content/ql-cache/quicklatex.com-87bc95df0033834bba0398b8421faac5_l3.png "Rendered by QuickLaTeX.com")
![\displaystyle \begin{vmatrix} 3 & -1 \\[1.1ex] 1 & 2 \end{vmatrix} = 7 \neq 0](https://mathority.org/wp-content/ql-cache/quicklatex.com-b9805283b75e2b89f67c7865a1263112_l3.png "Rendered by QuickLaTeX.com")
Donc la matrice A est de rang 2 :
Une fois que nous connaissons le rang de A, nous calculons le rang de A’. On sait déjà que le déterminant des 3 premières colonnes donne 0, on essaie donc les autres déterminants 3×3 possibles :
![\displaystyle \begin{vmatrix}-1 & 2 & 1 \\[1.1ex] 2 & -2 & 5 \\[1.1ex] -5 & 6 & -9\end{vmatrix} = 0 \quad \begin{vmatrix}3 & 2 & 1 \\[1.1ex] 1 & -2 & 5 \\[1.1ex] 1 & 6 & -9\end{vmatrix} = 0 \quad \begin{vmatrix} 3 & -1 & 1 \\[1.1ex] 1 & 2 & 5 \\[1.1ex] 1 & -5 & -9\end{vmatrix} = 0](https://mathority.org/wp-content/ql-cache/quicklatex.com-e6457fe3f03722b7f0d955191f318915_l3.png "Rendered by QuickLaTeX.com")
Tous les déterminants 3×3 de la matrice A’ sont 0, donc la matrice A’ ne sera pas non plus de rang 3. Cependant, à l’intérieur elle a bien des déterminants d’ordre 2 différents de 0. Par exemple :
![\displaystyle \begin{vmatrix} -1 & 2 \\[1.1ex] 2 & -2 \end{vmatrix} = -2 \neq 0](https://mathority.org/wp-content/ql-cache/quicklatex.com-eafa4747802fae3f0c36350357abbeb2_l3.png "Rendered by QuickLaTeX.com")
Donc la matrice A’ sera de rang 2 :
Le rang de la matrice A est égal au rang de la matrice A’ mais ces deux sont inférieurs au nombre d’inconnues du système (3). Par conséquent, par le théorème de Rouché-Frobenius, nous savons qu’il s’agit d’un système compatible indéterminé (SCI):
Exercice 3
Déterminez quel type de système est le système d’équations suivant en utilisant le théorème de Rouché-Frobenius :
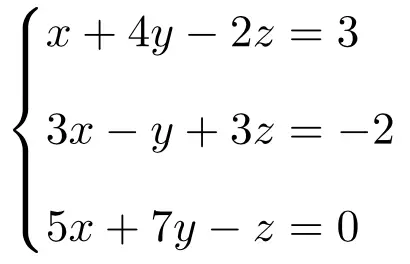
On fait d’abord la matrice A et la matrice étendue A’ du système :
![\displaystyle A= \left( \begin{array}{ccc} 1 & 4 & -2 \\[1.1ex] 3 & -1 & 3 \\[1.1ex] 5 & 7 & -1 \end{array} \right) \qquad A'= \left( \begin{array}{ccc|c} 1 & 4 & -2 & 3 \\[1.1ex] 3 & -1 & 3 & -2 \\[1.1ex] 5 & 7 & -1 & 0 \end{array} \right)](https://mathority.org/wp-content/ql-cache/quicklatex.com-1820d31e4fd5c79804c9b6fa15abb469_l3.png "Rendered by QuickLaTeX.com")
Calculons maintenant la plage de la matrice A :
![\displaystyle \begin{vmatrix}A \end{vmatrix}= \begin{vmatrix} 1 & 4 & -2 \\[1.1ex] 3 & -1 & 3 \\[1.1ex] 5 & 7 & -1\end{vmatrix} = 0](https://mathority.org/wp-content/ql-cache/quicklatex.com-4f998260ee4c96673085ea6fd4ca87ba_l3.png "Rendered by QuickLaTeX.com")
![\displaystyle \begin{vmatrix} 1 & 4 \\[1.1ex] 3 & -1 \end{vmatrix} = -13 \neq 0](https://mathority.org/wp-content/ql-cache/quicklatex.com-159a1c58fdcd972b4b08e4795950e064_l3.png "Rendered by QuickLaTeX.com")
Donc la matrice A est de rang 2 :
Une fois que nous connaissons le rang de A, nous calculons le rang de A’. On sait déjà que le déterminant des 3 premières colonnes donne 0, mais pas le déterminant des 3 dernières colonnes :
![\displaystyle \begin{vmatrix} 4 & -2 & 3 \\[1.1ex]-1 & 3 & -2 \\[1.1ex] 7 & -1 & 0 \end{vmatrix} = -40 \neq 0](https://mathority.org/wp-content/ql-cache/quicklatex.com-c673a5bbbd41933208169fa3e08b7c62_l3.png "Rendered by QuickLaTeX.com")
Donc, la matrice A’ est de rang 3 :
Le rang de la matrice A est plus petit que le rang de la matrice A’, on peut donc déduire du théorème de Rouché-Frobenius qu’il s’agit d’un Système Incompatible (SI) :
Exercice 4
Déterminer le type du système d’équations à 3 inconnues suivant à l’aide du théorème de Rouché-Frobenius :
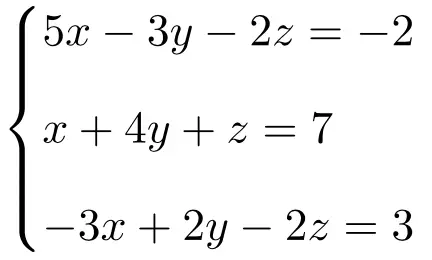
On fait d’abord la matrice A et la matrice étendue A’ du système :
![\displaystyle A= \left( \begin{array}{ccc} 5 & -3 & -2 \\[1.1ex] 1 & 4 & 1 \\[1.1ex]-3 & 2 & -2 \end{array} \right) \qquad A'= \left( \begin{array}{ccc|c} 5 & -3 & -2 & -2 \\[1.1ex] 1 & 4 & 1 & 7 \\[1.1ex]-3 & 2 & -2 & 3 \end{array} \right)](https://mathority.org/wp-content/ql-cache/quicklatex.com-f8a0454c53a64f612c689ba1dae1196b_l3.png "Rendered by QuickLaTeX.com")
Il faut maintenant calculer le rang de la matrice A. Pour cela, on résout le déterminant de la matrice avec la règle de Sarrus :
![\displaystyle \begin{vmatrix}A \end{vmatrix}= \begin{vmatrix} 5 & -3 & -2 \\[1.1ex] 1 & 4 & 1 \\[1.1ex]-3 & 2 & -2 \end{vmatrix} = -40+9-4-24-10-6=-75 \bm{\neq 0}](https://mathority.org/wp-content/ql-cache/quicklatex.com-420f0d1ee000f39cbfbce88bf122f413_l3.png "Rendered by QuickLaTeX.com")
La matrice ayant un déterminant de troisième ordre différent de 0, la matrice A est de rang 3 :
Donc, la matrice A’ est aussi de rang 3 , puisqu’elle est toujours au moins de rang A et elle ne peut pas être de rang 4 car on ne peut résoudre aucun déterminant 4×4.
Ainsi, grâce à l’application du théorème de Rouché-Frobenius, nous savons que le système est un Système Déterminé Compatible (SCD), car la plage de A est égale à la plage de A’ et au nombre d’inconnues.
Exercice 5
Identifiez quel type de système est le système d’équations suivant grâce au théorème de Rouché-Frobenius :
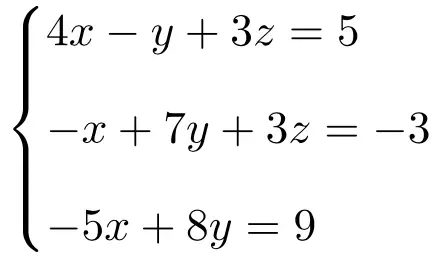
On fait d’abord la matrice A et la matrice étendue A’ du système :
![\displaystyle A= \left( \begin{array}{ccc} 4 & -1 & 3 \\[1.1ex] -1 & 7 & 3 \\[1.1ex] -5 & 8 & 0 \end{array} \right) \qquad A'= \left( \begin{array}{ccc|c} 4 & -1 & 3 & 5 \\[1.1ex] -1 & 7 & 3 & -3 \\[1.1ex] -5 & 8 & 0 & 9 \end{array} \right)](https://mathority.org/wp-content/ql-cache/quicklatex.com-3211e276b2b040969c38bc6c69eabd52_l3.png "Rendered by QuickLaTeX.com")
Calculons maintenant la plage de la matrice A :
![\displaystyle \begin{vmatrix}A \end{vmatrix}= \begin{vmatrix} 4 & -1 & 3 \\[1.1ex] -1 & 7 & 3 \\[1.1ex] -5 & 8 & 0\end{vmatrix} = 0](https://mathority.org/wp-content/ql-cache/quicklatex.com-21004095a3a8ef3edfc15bed5c7853a4_l3.png "Rendered by QuickLaTeX.com")
![\displaystyle \begin{vmatrix} 4 & -1 \\[1.1ex] -1 & 7 \end{vmatrix} = 27 \neq 0](https://mathority.org/wp-content/ql-cache/quicklatex.com-a58059046b56cf1f8d82c6c8939e44ca_l3.png "Rendered by QuickLaTeX.com")
La matrice A est donc de rang 2 :
Une fois que nous connaissons le rang de A, nous calculons le rang de A’. Le déterminant des 3 premières colonnes que nous connaissons déjà donne 0, mais le déterminant des 3 dernières colonnes ne donne pas :
![\displaystyle \begin{vmatrix} -1 & 3 & 5 \\[1.1ex] 7 & 3 & -3 \\[1.1ex] 8 & 0 & 9\end{vmatrix} = -408 \neq 0](https://mathority.org/wp-content/ql-cache/quicklatex.com-992718d3b50aedf77c80c262fad5845f_l3.png "Rendered by QuickLaTeX.com")
Donc, la matrice A’ est de rang 3 :
Et, enfin, on applique le domaine au théorème de Rouché-Frobenius : le domaine de la matrice A est plus petit que le domaine de la matrice A’, c’est donc un Système Incompatible (SI) :
Exercice 6
Classifier le système d’équations d’ordre 3 suivant avec le théorème de Rouché-Frobenius :
![\begin{cases} 6x-2y+4z=1 \\[1.5ex] -2x+4y+3z= 7 \\[1.5ex] 8x-6y+z = -6\end{cases}](https://mathority.org/wp-content/ql-cache/quicklatex.com-d45e8bc425b08e403a98e01693201681_l3.png "Rendered by QuickLaTeX.com")
On construit tout d’abord la matrice A et la matrice étendue A’ du système :
![\displaystyle A= \left( \begin{array}{ccc} 6 & -2 & 4 \\[1.1ex] -2 & 4 & 3 \\[1.1ex] 8 & -6 & 1 \end{array} \right) \qquad A'= \left( \begin{array}{ccc|c} 6 & -2 & 4 & 1 \\[1.1ex] -2 & 4 & 3 & 7 \\[1.1ex] 8 & -6 & 1 & -6 \end{array} \right)](https://mathority.org/wp-content/ql-cache/quicklatex.com-8e779eca9135adc44e4a3a55f368560f_l3.png "Rendered by QuickLaTeX.com")
Calculons maintenant la plage de la matrice A :
![\displaystyle \begin{vmatrix}A \end{vmatrix}= \begin{vmatrix} 6 & -2 & 4 \\[1.1ex] -2 & 4 & 3 \\[1.1ex] 8 & -6 & 1 \end{vmatrix} = 0](https://mathority.org/wp-content/ql-cache/quicklatex.com-c2f63f79858eae462547cf2f270fc780_l3.png "Rendered by QuickLaTeX.com")
![\displaystyle \begin{vmatrix} 6 & -2 \\[1.1ex] -2 & 4 \end{vmatrix} = 20 \neq 0](https://mathority.org/wp-content/ql-cache/quicklatex.com-e5fa293b94b8c6acfd998f1e154abf7a_l3.png "Rendered by QuickLaTeX.com")
Donc la matrice A est de rang 2 :
Une fois que nous connaissons le rang de A, nous calculons le rang de A’. On sait déjà que le déterminant des 3 premières colonnes donne 0, on essaie donc les autres déterminants 3×3 possibles :
![\displaystyle \begin{vmatrix} -2 & 4 & 1 \\[1.1ex]4 & 3 & 7 \\[1.1ex] -6 & 1 & -6\end{vmatrix} = 0 \quad \begin{vmatrix}6 & 4 & 1 \\[1.1ex] -2 & 3 & 7 \\[1.1ex] 8 & 1 & -6\end{vmatrix} = 0 \quad \begin{vmatrix} 6 & -2 & 1 \\[1.1ex] -2 & 4 & 7 \\[1.1ex] 8 & -6 & -6\end{vmatrix} = 0](https://mathority.org/wp-content/ql-cache/quicklatex.com-98958f866454a1bf9f1ac078562065cd_l3.png "Rendered by QuickLaTeX.com")
Tous les déterminants 3×3 de la matrice A’ sont 0, donc la matrice A’ ne sera pas non plus de rang 3. Cependant, à l’intérieur elle a bien des déterminants d’ordre 2 différents de 0. Par exemple :
![\displaystyle \begin{vmatrix} 6 & -2 \\[1.1ex] -2 & 4 \end{vmatrix} = 20 \neq 0](https://mathority.org/wp-content/ql-cache/quicklatex.com-58091f1a37a4ef81fdf56f01dd9531a3_l3.png "Rendered by QuickLaTeX.com")
Donc la matrice A’ sera de rang 2 :
Enfin, en appliquant le théorème de Rouché-Frobenius, on sait qu’il s’agit d’un Système Compatible Indéterminé (SCI), car la plage de la matrice A est égale à la plage de la matrice A’ mais ces deux sont plus petites que le nombre d’inconnues du système (3):