Sur cette page, vous apprendrez ce qu’est la méthode de Gauss-Jordan et comment résoudre un système d’équations à l’aide de la méthode de Gauss. De plus, vous trouverez également des exemples et des exercices résolus de systèmes avec la méthode de Gauss afin que vous puissiez la pratiquer et la comprendre parfaitement.
Qu’est-ce que la méthode de Gauss ?
La méthode de Gauss-Jordan est une procédure utilisée pour résoudre des systèmes d’équations à 3 inconnues, c’est-à-dire comme ceci :
![Rendered by QuickLaTeX.com \left. \begin{array}{r} 3x-4y+5z=10 \\[2ex] x+5y-2z=4 \\[2ex] -x+4y+2z=-1 \end{array} \right\}](https://mathority.org/wp-content/ql-cache/quicklatex.com-088146ef83bbd007e82aca8189434c25_l3.png)
L’objectif de la méthode de Gauss est de convertir le système d’équations initial en un système étagé , c’est-à-dire un système dans lequel chaque équation a une inconnue de moins que la précédente :
![Rendered by QuickLaTeX.com \left. \begin{array}{r} a_1x+b_1y+c_1z=d_1 \\[2ex] a_2x+b_2y+c_2z=d_2 \\[2ex] a_3x+b_3y+c_3z=d_3 \end{array} \right\} \ \bm{\longrightarrow} \left. \begin{array}{r} A_1x+B_1y+C_1z=D_1 \\[2ex] B_2y+C_2z=D_2 \\[2ex] C_3z=D_3 \end{array} \right\}](https://mathority.org/wp-content/ql-cache/quicklatex.com-10926b0856ae512c737ae924bd9413a1_l3.png)
Cependant, pour ce faire, il faut d’abord savoir exprimer un système d’équations sous forme matricielle et les transformations permises sur cette matrice. Nous expliquerons donc ces deux choses avant, puis nous verrons comment utiliser la procédure de la méthode de Gauss .
Matrice étendue au système
Avant de voir comment se résout le système, il faut savoir qu’un système d’équations peut s’exprimer sous la forme d’une matrice : les coefficients des
![]() sont mis dans la première colonne, les coefficients des
sont mis dans la première colonne, les coefficients des![]() dans la deuxième colonne, les coefficients de la
dans la deuxième colonne, les coefficients de la![]() dans la troisième colonne et les nombres sans inconnue dans la quatrième colonne.
dans la troisième colonne et les nombres sans inconnue dans la quatrième colonne.
Par exemple:
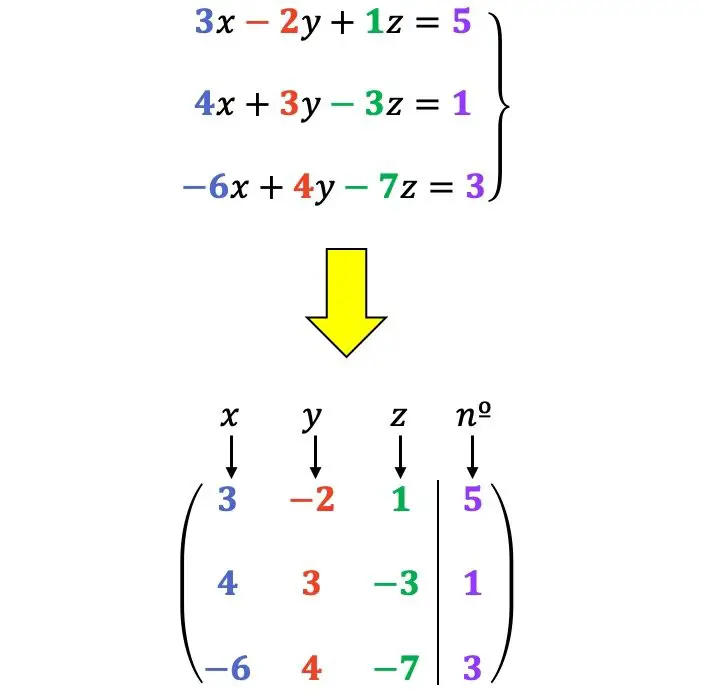
Transformations de lignes autorisées
Afin de convertir le système d’équations en un système échelonné, l’une des opérations suivantes peut être effectuée sur la matrice associée au système :
- Modifiez l’ordre des lignes dans la matrice.
Par exemple, on peut changer l’ordre des lignes 2 et 3 d’une matrice :
![Rendered by QuickLaTeX.com \left( \begin{array}{ccc|c} 3 & 5 & -2 & 1 \\[2ex] -2 & 4 & -1 & 2 \\[2ex] 6 & 1 & -3 & 10 \end{array} \right) \begin{array}{c} \\[2ex] \xrightarrow{ f_2 \rightarrow f_3}} \\[2ex] \xrightarrow{ f_3 \rightarrow f_2}} \end{array} \left( \begin{array}{ccc|c} 3 & 5 & -2 & 1 \\[2ex] 6 & 1 & -3 & 10 \\[2ex] -2 & 4 & -1 & 2 \end{array} \right)](https://mathority.org/wp-content/ql-cache/quicklatex.com-ee0e251559ef9dfd02c9b0105f934af8_l3.png)
- Multipliez ou divisez tous les termes d’une ligne par un nombre autre que 0.
Par exemple, nous pouvons multiplier la ligne 1 par 4 et diviser la ligne 3 par 2 :
![Rendered by QuickLaTeX.com \left( \begin{array}{ccc|c} 1 & -2 & 3 & 1 \\[2ex] 3 & -1 & 5 & -3 \\[2ex] 2 & -4 & -2 & 6 \end{array} \right) \begin{array}{c} \xrightarrow{4 f_1} \\[2ex] \\[2ex] \xrightarrow{ f_3 / 2} \end{array} \left( \begin{array}{ccc|c} 4 & -8 & 12 & 4 \\[2ex] 3 & -1 & 5 & -3 \\[2ex] 1 & -2 & -1 & 3 \end{array} \right)](https://mathority.org/wp-content/ql-cache/quicklatex.com-0e1f081c9056075ede064b2e5c9e4193_l3.png)
- Remplacez une ligne par la somme de la même ligne plus une autre ligne multipliée par un nombre.
Par exemple, dans la matrice suivante, nous ajoutons la ligne 2 à la ligne 3 multipliée par 1 :
![Rendered by QuickLaTeX.com \left( \begin{array}{ccc|c} -1 & -3 & 4 & 1 \\[2ex] 2 & 4 & 1 & -5 \\[2ex] 1 & -2 & 3 & -1 \end{array} \right) \begin{array}{c} \\[2ex] \xrightarrow{f_2 + 1 \cdot f_3} \\[2ex] & \end{array} \left( \begin{array}{ccc|c} -1 & -3 & 4 & 1 \\[2ex] 3 & 2 & 4 & -6 \\[2ex] 1 & -2 & 3 & -1 \end{array} \right)](https://mathority.org/wp-content/ql-cache/quicklatex.com-04417e2094ac05c7a374334c55197f36_l3.png)
Comment résoudre un système d’équations par la méthode de Gauss ?
Nous allons maintenant voir à travers un exemple la procédure de résolution d’un système d’équations avec la méthode de Gauss :
![Rendered by QuickLaTeX.com \left. \begin{array}{r} -x+2y+2z=-24 \\[2ex] x+y+z=48 \\[2ex] 2x-6y+4z=12 \end{array} \right\}](https://mathority.org/wp-content/ql-cache/quicklatex.com-61e6e829301e6730c9e27f9c0a30de2e_l3.png)
La première chose à faire est la matrice étendue du système :
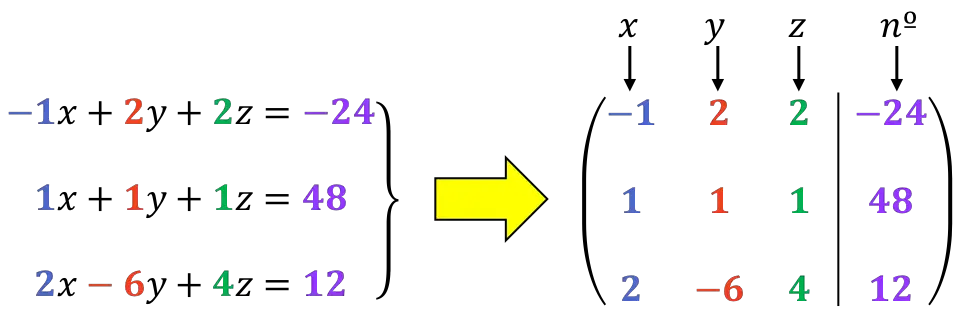
Comme nous le verrons plus tard, il vaut mieux que le premier chiffre de la première ligne soit un 1. Nous allons donc changer l’ordre des lignes 1 et 2 :
![Rendered by QuickLaTeX.com \left( \begin{array}{ccc|c} -1 & 2 & 2 &-24 \\[2ex] 1 & 1 & 1 & 48 \\[2ex] 2 & -6 & 4 & 12 \end{array} \right) \begin{array}{c} \xrightarrow{ f_1 \rightarrow f_2} \\[2ex] \xrightarrow{ f_2 \rightarrow f_1} \\[2ex] & \end{array} \left( \begin{array}{ccc|c} \color{blue}\boxed{\color{black}1} & 1 & 1 & 48 \\[2ex] -1 & 2 & 2 &-24 \\[2ex] 2 & -6 & 4 & 12 \end{array} \right)](https://mathority.org/wp-content/ql-cache/quicklatex.com-b45e0f757ca2880442314f6a4800697b_l3.png)
Le but de la méthode de Gauss est de faire en sorte que les nombres sous la diagonale principale soient 0 . Autrement dit, nous devons convertir les nombres rouges en 0 :
![Rendered by QuickLaTeX.com \left( \begin{array}{ccc|c} 1 & 1 & 1 & 48 \\[2ex] \color{red}\bm{-1} & 2 & 2 &-24 \\[2ex] \color{red}\bm{2} & \color{red}\bm{-6} & 4 & 12 \end{array} \right)](https://mathority.org/wp-content/ql-cache/quicklatex.com-28164ac6b48d32c09b4725548c0633f6_l3.png)
Pour éliminer ces nombres, nous devons effectuer les transformations appropriées des lignes.
Par exemple, le -1, qui est le premier élément de la deuxième ligne, est le négatif de 1, le premier élément de la première ligne. Par conséquent, si nous ajoutons la première ligne à la deuxième ligne, le -1 sera éliminé :

Donc, si nous faisons cette somme, nous nous retrouvons avec la matrice suivante :
![Rendered by QuickLaTeX.com \left( \begin{array}{ccc|c} 1 & 1 & 1 & 48 \\[2ex] -1 & 2 & 2 & -24 \\[2ex] 2 & -6 & 4 & 12 \end{array} \right) \begin{array}{c} \\[2ex] \xrightarrow{f_2 + f_1} \\[2ex] & \end{array} \left( \begin{array}{ccc|c} 1 & 1 & 1 & 48 \\[2ex] \color{blue}\boxed{\color{black}0} & 3 & 3 & 24 \\[2ex] 2 & -6 & 4 & 12 \end{array} \right)](https://mathority.org/wp-content/ql-cache/quicklatex.com-1b106306b92bfc3e99d602c22d5198bd_l3.png)
De cette façon, nous avons réussi à transformer -1 en un 0.
Maintenant, nous allons transformer le 2. Si vous remarquez, le 2, qui est le premier élément de la troisième ligne, est le double de 1, le premier élément de la première ligne. Par conséquent, si nous ajoutons la première ligne multipliée par -2 à la troisième ligne, le 2 sera éliminé :
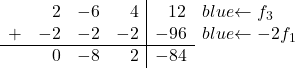
On se retrouve donc avec la matrice suivante :
![Rendered by QuickLaTeX.com \left( \begin{array}{ccc|c} 1 & 1 & 1 & 48 \\[2ex] 0 & 3 & 3 & 24 \\[2ex] 2 & -6 & 4 & 12 \end{array} \right) \begin{array}{c} \\[2ex] \\[2ex] \xrightarrow{f_3-2f_1} \end{array} \left( \begin{array}{ccc|c} 1 & 1 & 1 & 48 \\[2ex] 0 & 3 & 3 & 24 \\[2ex] \color{blue}\boxed{\color{black}0} & -8 & 2 & -84 \end{array} \right)](https://mathority.org/wp-content/ql-cache/quicklatex.com-36b2fdf8de855cf35049ecefcf7c1da5_l3.png)
De cette façon, nous avons réussi à transformer le 2 en un 0.
Il ne nous reste plus qu’à convertir le -8 en 0. Pour ce faire, nous multiplions la troisième ligne par 3 et ajoutons la deuxième ligne multipliée par 8 :
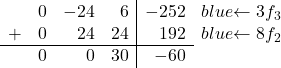
On obtient donc la matrice suivante :
![Rendered by QuickLaTeX.com \left( \begin{array}{ccc|c} 1 & 1 & 1 & 48 \\[2ex] 0 & 3 & 3 & 24 \\[2ex] 0 & -8 & 2 & -84 \end{array} \right) \begin{array}{c} \\[2ex] \\[2ex] \xrightarrow{3f_3 + 8f_2} \end{array} \left( \begin{array}{ccc|c} 1 & 1 & 1 & 48 \\[2ex] 0 & 3 & 3 & 24 \\[2ex] 0 & \color{blue}\boxed{\color{black}0} & 30 & -60 \end{array} \right)](https://mathority.org/wp-content/ql-cache/quicklatex.com-6e2324629222c746a9021ce05ba7d54d_l3.png)
Et avec ces transformations, nous avons obtenu que tous les nombres sous la diagonale principale soient 0. Nous pouvons donc maintenant résoudre le système d’équations.
Il faut maintenant convertir la matrice en un système d’équations à inconnues . Pour ce faire, rappelez-vous que la première colonne correspond à la
![]() , la deuxième colonne du
, la deuxième colonne du![]() , la troisième colonne du
, la troisième colonne du![]() et la dernière colonne sont les nombres sans inconnues :
et la dernière colonne sont les nombres sans inconnues :
![Rendered by QuickLaTeX.com \left( \begin{array}{ccc|c} 1 & 1 & 1 & 48 \\[2ex] 0 & 3 & 3 & 24 \\[2ex] 0 & 0 & 30 & -60 \end{array} \right) \ \longrightarrow \ \left. \begin{array}{r} 1x+1y+1z=48 \\[2ex] 3y+3z=24 \\[2ex] 30z=-60 \end{array} \right\}](https://mathority.org/wp-content/ql-cache/quicklatex.com-6f90de9d9f5a06959a2d4aebf05f4758_l3.png)
Et, enfin, pour résoudre le système, nous devons résoudre les inconnues des équations de bas en haut. Puisque la dernière équation n’a qu’une seule inconnue, nous pouvons donc la résoudre et trouver sa valeur :
![]()
![]()
![]()
Maintenant que nous savons ce qu’est z, si nous substituons sa valeur dans la deuxième équation, nous pouvons trouver la valeur de
![]() :
:
![]()
![]()
![]()
![]()
![]()
![]()
Et on fait de même avec la première équation : on substitue les valeurs des autres inconnues et on efface
![]() :
:
![]()
![]()
![]()
![]()
La solution du système d’équations est donc :
![]()
Problèmes résolus de systèmes d’équations par la méthode de Gauss-Jordan
Exercice 1
Résolvez le système d’équations suivant en utilisant la méthode de Gauss :
![Rendered by QuickLaTeX.com \left. \begin{array}{r} x+y-z=2 \\[2ex] x-2y+3z=0 \\[2ex] 2x-y+3z=3 \end{array} \right\}](https://mathority.org/wp-content/ql-cache/quicklatex.com-854043b0e7e3e2166593dcf5c645bfa0_l3.png)
La première chose que nous devons faire est la matrice étendue du système :
![Rendered by QuickLaTeX.com \left. \begin{array}{r} x+y-z=2 \\[2ex] x-2y+3z=0 \\[2ex] 2x-y+3z=3 \end{array} \right\} \longrightarrow \left( \begin{array}{ccc|c} 1 & 1 & -1 & 2 \\[2ex] 1 & -2 & 3 & 0 \\[2ex] 2 & -1 & 3 & 3 \end{array} \right)](https://mathority.org/wp-content/ql-cache/quicklatex.com-1b6369a58b91f31bf4c8bc212ccf68c6_l3.png)
Maintenant, nous devons faire en sorte que tous les nombres sous le tableau principal soient 0.
Nous effectuons donc des opérations de ligne pour annuler les deux derniers termes de la première colonne :
![Rendered by QuickLaTeX.com \left( \begin{array}{ccc|c}1 & 1 & -1 & 2 \\[2ex] 1 & -2 & 3 & 0 \\[2ex] 2 & -1 & 3 & 3 \end{array} \right) \begin{array}{c} \\[2ex] \xrightarrow{f_2 -f_1} \\[2ex] \xrightarrow{f_3-2f_1} & \end{array} \left( \begin{array}{ccc|c} 1 & 1 & -1 & 2 \\[2ex] 0 & -3 & 4 & -2 \\[2ex] 0 & -3 & 5 & -1 \end{array} \right)](https://mathority.org/wp-content/ql-cache/quicklatex.com-cd42dcf61aebc4c67de13e09dff72f4b_l3.png)
Maintenant, nous supprimons le dernier élément de la deuxième colonne :
![Rendered by QuickLaTeX.com \left( \begin{array}{ccc|c}1 & 1 & -1 & 2 \\[2ex] 0 & -3 & 4 & -2 \\[2ex] 0 & -3 & 5 & -1 \end{array} \right) \begin{array}{c} \\[2ex] \\[2ex] \xrightarrow{f_3-f_2} & \end{array} \left( \begin{array}{ccc|c} 1 & 1 & -1 & 2 \\[2ex] 0 & -3 & 4 & -2 \\[2ex] 0 & 0 & 1 & 1 \end{array} \right)](https://mathority.org/wp-content/ql-cache/quicklatex.com-13945337848a6f1badf6efe249951124_l3.png)
Une fois que tous les nombres sous la diagonale principale sont 0, nous pouvons maintenant résoudre le système d’équations. Pour ce faire, on exprime à nouveau la matrice sous la forme d’un système d’équations à inconnues :
![Rendered by QuickLaTeX.com \left( \begin{array}{ccc|c} 1 & 1 & -1 & 2 \\[2ex] 0 & -3 & 4 & -2 \\[2ex] 0 & 0 & 1 & 1 \end{array} \right) \ \longrightarrow \ \left. \begin{array}{r} x+y-z=2 \\[2ex] -3y+4z=-2 \\[2ex] 1z=1 \end{array} \right\}](https://mathority.org/wp-content/ql-cache/quicklatex.com-f068c276aae018a668cc005bcad3e641_l3.png)
Et on résout les inconnues des équations de bas en haut. On résout d’abord la dernière équation :
![]()
![]()
Maintenant, nous substituons la valeur de z dans la deuxième équation pour trouver la valeur de y :
![]()
![]()
![]()
![]()
![]()
Et on fait de même avec la première équation : on substitue les valeurs des autres inconnues et on résout pour x :
![]()
![]()
![]()
![]()
La solution du système d’équations est donc :
![]()
Exercice 2
Trouver la solution du système d’équations suivant par la méthode de Gauss :
![Rendered by QuickLaTeX.com \left. \begin{array}{r} 2x+y+2z=-3 \\[2ex] x+3y+2z=5 \\[2ex] 4x+2y-z=-1 \end{array} \right\}](https://mathority.org/wp-content/ql-cache/quicklatex.com-7d0595899b8137f769c74fce1b21286b_l3.png)
La première chose que nous devons faire est la matrice étendue du système :
![Rendered by QuickLaTeX.com \left. \begin{array}{r} 2x+y+2z=-3 \\[2ex] x+3y+2z=5 \\[2ex] 4x+2y-z=-1 \end{array} \right\} \longrightarrow \left( \begin{array}{ccc|c} 2 & 1 & 2 & -3 \\[2ex] 1 & 3 & 2 & 5 \\[2ex] 4 & 2 & -1 & -1 \end{array} \right)](https://mathority.org/wp-content/ql-cache/quicklatex.com-5e2a16b6d1451520bd8898675c022dc2_l3.png)
Pour appliquer la méthode de Gauss, c’est plus simple si le premier nombre de la première ligne est un 1. Nous allons donc changer l’ordre des lignes 1 et 2 :
![Rendered by QuickLaTeX.com \left( \begin{array}{ccc|c}2 & 1 & 2 & -3 \\[2ex] 1 & 3 & 2 & 5 \\[2ex] 4 & 2 & -1 & -1 \end{array} \right) \begin{array}{c} \xrightarrow{f_1\rightarrow f_2} \\[2ex] \xrightarrow{f_2\rightarrow f_1} \\[2ex] & \end{array} \left( \begin{array}{ccc|c}1 & 3 & 2 & 5 \\[2ex] 2 & 1 & 2 & -3 \\[2ex] 4 & 2 & -1 & -1\end{array} \right)](https://mathority.org/wp-content/ql-cache/quicklatex.com-ef7e2e42d0eecb0395afb7c8311b2ade_l3.png)
Maintenant, nous devons faire en sorte que tous les nombres sous le tableau principal soient 0.
Nous effectuons donc des opérations sur les lignes pour remplacer les deux derniers éléments de la première colonne :
![Rendered by QuickLaTeX.com \left( \begin{array}{ccc|c} 1 & 3 & 2 & 5 \\[2ex] 2 & 1 & 2 & -3 \\[2ex] 4 & 2 & -1 & -1 \end{array} \right) \begin{array}{c} \\[2ex] \xrightarrow{f_2 -2f_1} \\[2ex] \xrightarrow{f_3-4f_1} & \end{array} \left( \begin{array}{ccc|c} 1 & 3 & 2 & 5 \\[2ex] 0 & -5 & -2 & -13 \\[2ex] 0 & -10 & -9 & -21 \end{array} \right)](https://mathority.org/wp-content/ql-cache/quicklatex.com-40baaee3bbde9ed1577e00bc1c3b338f_l3.png)
Maintenant, nous convertissons le dernier élément de la deuxième colonne en zéro :
![Rendered by QuickLaTeX.com \left( \begin{array}{ccc|c}1 & 3 & 2 & 5 \\[2ex] 0 & -5 & -2 & -13 \\[2ex] 0 & -10 & -9 & -21\end{array} \right) \begin{array}{c} \\[2ex] \\[2ex] \xrightarrow{f_3-2f_2} & \end{array} \left( \begin{array}{ccc|c} 1 & 3 & 2 & 5 \\[2ex] 0 & -5 & -2 & -13 \\[2ex] 0 & 0 & -5 & 5 \end{array} \right)](https://mathority.org/wp-content/ql-cache/quicklatex.com-f328906485bfe6ee77833c04869e1240_l3.png)
Une fois que tous les nombres sous la diagonale principale sont 0, nous pouvons résoudre le système d’équations. Pour ce faire, on exprime à nouveau la matrice sous la forme d’un système d’équations à inconnues :
![Rendered by QuickLaTeX.com \left( \begin{array}{ccc|c} 1 & 3 & 2 & 5 \\[2ex] 0 & -5 & -2 & -13 \\[2ex] 0 & 0 & -5 & 5 \end{array} \right) \ \longrightarrow \ \left. \begin{array}{r} x+3y+2z=5 \\[2ex] -5y-2z=-13 \\[2ex] -5z=5 \end{array} \right\}](https://mathority.org/wp-content/ql-cache/quicklatex.com-a7e129715c720218a5cb25ef07442442_l3.png)
Et on résout les inconnues des équations de bas en haut. On résout d’abord la dernière équation :
![]()
![]()
Maintenant, nous substituons la valeur de z dans la deuxième équation pour trouver la valeur de y :
![]()
![]()
![]()
![]()
![]()
Et on fait de même avec la première équation : on substitue les valeurs des autres inconnues et on résout pour x :
![]()
![]()
![]()
![]()
La solution du système d’équations est donc :
![]()
Exercice 3
Calculez la solution du système d’équations suivant par la méthode de Gauss :
![Rendered by QuickLaTeX.com \left. \begin{array}{r} 2x+3y+z=-1 \\[2ex] 6x+4y+4z=0 \\[2ex] -4x+2y-z=5 \end{array} \right\}](https://mathority.org/wp-content/ql-cache/quicklatex.com-4301eae3179543fbdee7568e8f88aa4c_l3.png)
La première chose que nous devons faire est la matrice étendue du système :
![Rendered by QuickLaTeX.com \left. \begin{array}{r} 2x+3y+z=-1 \\[2ex] 6x+4y+4z=0 \\[2ex] -4x+2y-z=5\end{array} \right\} \longrightarrow \left( \begin{array}{ccc|c} 2 & 3 & 1 & -1 \\[2ex] 6 & 4 & 4 & 0 \\[2ex] -4 & 2 & -1 & 5 \end{array} \right)](https://mathority.org/wp-content/ql-cache/quicklatex.com-c0d96160d6670e817dd39f61816e1e6e_l3.png)
Maintenant, nous devons rendre tous les nombres sous le tableau parent 0.
Nous effectuons donc des opérations sur les lignes pour remplacer les deux derniers éléments de la première colonne :
![Rendered by QuickLaTeX.com \left( \begin{array}{ccc|c} 2 & 3 & 1 & -1 \\[2ex] 6 & 4 & 4 & 0 \\[2ex] -4 & 2 & -1 & 5\end{array} \right) \begin{array}{c} \\[2ex] \xrightarrow{f_2 -3f_1} \\[2ex] \xrightarrow{f_3+2f_1} & \end{array} \left( \begin{array}{ccc|c} 2 & 3 & 1 & -1 \\[2ex] 0 & -5 & 1 & 3 \\[2ex] 0 & 8 & 1 & 3\end{array} \right)](https://mathority.org/wp-content/ql-cache/quicklatex.com-87853177b6be449178c24e414dc0865a_l3.png)
Maintenant, nous convertissons le dernier élément de la deuxième colonne en zéro :
![Rendered by QuickLaTeX.com \left( \begin{array}{ccc|c}2 & 3 & 1 & -1 \\[2ex] 0 & -5 & 1 & 3 \\[2ex] 0 & 8 & 1 & 3\end{array} \right) \begin{array}{c} \\[2ex] \\[2ex] \xrightarrow{5f_3+8f_2} & \end{array} \left( \begin{array}{ccc|c} 2 & 3 & 1 & -1 \\[2ex] 0 & -5 & 1 & 3 \\[2ex] 0 & 0 & 13 & 39 \end{array} \right)](https://mathority.org/wp-content/ql-cache/quicklatex.com-c4105ceb64b201c532109f8639bdefde_l3.png)
Une fois que tous les nombres sous la diagonale principale sont 0, nous pouvons résoudre le système d’équations. Pour ce faire, on exprime à nouveau la matrice sous la forme d’un système d’équations à inconnues :
![Rendered by QuickLaTeX.com \left( \begin{array}{ccc|c} 2 & 3 & 1 & -1 \\[2ex] 0 & -5 & 1 & 3 \\[2ex] 0 & 0 & 13 & 39\end{array} \right) \ \longrightarrow \ \left. \begin{array}{r} 2x+3y+1z=-1 \\[2ex] -5y+z=3 \\[2ex] 13z=39 \end{array} \right\}](https://mathority.org/wp-content/ql-cache/quicklatex.com-faae83295a3f7b3d8b6d76f78d56fac6_l3.png)
Et on résout les inconnues des équations de bas en haut. On résout d’abord la dernière équation :
![]()
![]()
Maintenant, nous substituons la valeur de z dans la deuxième équation pour trouver la valeur de y :
![]()
![]()
![]()
![]()
Et on fait de même avec la première équation : on substitue les valeurs des autres inconnues et on résout pour x :
![]()
![]()
![]()
![]()
![]()
La solution du système d’équations est donc :
![]()
Exercice 4
Résoudre le système d’équations à 3 inconnues suivant par la méthode de Gauss :
![Rendered by QuickLaTeX.com \left. \begin{array}{r} 2x-6=4y+6z \\[2ex] -y-3z=1-3x \\[2ex] -4x-y=6-3z \end{array} \right\}](https://mathority.org/wp-content/ql-cache/quicklatex.com-b005b2eda0d63c7130f2f5531c2ae4a0_l3.png)
Avant d’appliquer la méthode de Gauss, nous devons disposer le système d’équations de manière à ce que toutes les inconnues soient à gauche de l’équation et les nombres à droite :
![Rendered by QuickLaTeX.com \left. \begin{array}{r}2x-6=4y+6z \\[2ex] -y-3z=1-3x \\[2ex] -4x-y=6-3z \end{array} \right\} \longrightarrow \left. \begin{array}{r} 2x-4y-6z=6 \\[2ex] 3x-y-3z=1 \\[2ex] -4x-y+3z=6\end{array} \right\}](https://mathority.org/wp-content/ql-cache/quicklatex.com-1e0ca77b625e8f9e235ce8da4e4008df_l3.png)
Une fois le système commandé, on construit la matrice développée du système :
![Rendered by QuickLaTeX.com \left. \begin{array}{r} 2x-4y-6z=6 \\[2ex] 3x-y-3z=1 \\[2ex] -4x-y+3z=6 \end{array} \right\} \longrightarrow \left( \begin{array}{ccc|c} 2 & -4 & -6 & 6 \\[2ex] 3 & -1 & -3 & 1 \\[2ex] -4 & -1 & 3 & 6 \end{array} \right)](https://mathority.org/wp-content/ql-cache/quicklatex.com-b88e3ff141b847028a55ba4b46b8e870_l3.png)
Comme tous les nombres de la première rangée sont pairs, avant d’opérer avec les rangées nous allons diviser la première rangée par 2. Puisque cela facilitera les calculs :
![Rendered by QuickLaTeX.com \left( \begin{array}{ccc|c}2 & -4 & -6 & 6 \\[2ex] 3 & -1 & -3 & 1 \\[2ex] -4 & -1 & 3 & 6 \end{array} \right) \begin{array}{c} \xrightarrow{f_1/2} \\[2ex] \\[2ex] & \end{array} \left( \begin{array}{ccc|c}1 & -2 & -3 & 3 \\[2ex] 3 & -1 & -3 & 1 \\[2ex] -4 & -1 & 3 & 6\end{array} \right)](https://mathority.org/wp-content/ql-cache/quicklatex.com-b05235526cd8e44c16749606bfe8976c_l3.png)
Maintenant, nous devons faire en sorte que tous les nombres sous le tableau principal soient 0.
Nous effectuons donc des opérations sur les lignes pour remplacer les deux derniers éléments de la première colonne :
![Rendered by QuickLaTeX.com \left( \begin{array}{ccc|c} 1 & -2 & -3 & 3 \\[2ex] 3 & -1 & -3 & 1 \\[2ex] -4 & -1 & 3 & 6 \end{array} \right) \begin{array}{c} \\[2ex] \xrightarrow{f_2 -3f_1} \\[2ex] \xrightarrow{f_3+4f_1} & \end{array} \left( \begin{array}{ccc|c} 1 & -2 & -3 & 3 \\[2ex] 0 & 5 & 6 & -8 \\[2ex] 0 & -9 & -9 & 18\end{array} \right)](https://mathority.org/wp-content/ql-cache/quicklatex.com-3da82815d14fdfae0f61a8e1747fb9fe_l3.png)
Comme précédemment, puisque tous les nombres de la dernière ligne sont des multiples de 9, nous allons le diviser par 9 pour faciliter les calculs :
![Rendered by QuickLaTeX.com \left( \begin{array}{ccc|c}1 & -2 & -3 & 3 \\[2ex] 0 & 5 & 6 & -8 \\[2ex] 0 & -9 & -9 & 18 \end{array} \right) \begin{array}{c} \\[2ex] \\[2ex]\xrightarrow{f_3/9} & \end{array} \left( \begin{array}{ccc|c}1 & -2 & -3 & 3 \\[2ex] 0 & 5 & 6 & -8 \\[2ex] 0 & -1 & -1 & 2\end{array} \right)](https://mathority.org/wp-content/ql-cache/quicklatex.com-342000d19a7bd19e055a39695c79cb49_l3.png)
Maintenant, nous convertissons le dernier élément de la deuxième colonne en zéro :
![Rendered by QuickLaTeX.com \left( \begin{array}{ccc|c}1 & -2 & -3 & 3 \\[2ex] 0 & 5 & 6 & -8 \\[2ex] 0 & -1 & -1 & 2\end{array} \right) \begin{array}{c} \\[2ex] \\[2ex] \xrightarrow{5f_3+f_2} & \end{array} \left( \begin{array}{ccc|c} 1 & -2 & -3 & 3 \\[2ex] 0 & 5 & 6 & -8 \\[2ex] 0 & 0 & 1 & 2 \end{array} \right)](https://mathority.org/wp-content/ql-cache/quicklatex.com-2158e7f439f677617bb8a40695fb5711_l3.png)
Une fois que tous les nombres sous la diagonale principale sont 0, nous pouvons résoudre le système d’équations. Pour ce faire, on exprime à nouveau la matrice sous la forme d’un système d’équations à inconnues :
![Rendered by QuickLaTeX.com \left( \begin{array}{ccc|c} 1 & -2 & -3 & 3 \\[2ex] 0 & 5 & 6 & -8 \\[2ex] 0 & 0 & 1 & 2 \end{array} \right) \ \longrightarrow \ \left. \begin{array}{r} x-2y-3z=3 \\[2ex] 5y+6z=-8 \\[2ex] 1z=2 \end{array} \right\}](https://mathority.org/wp-content/ql-cache/quicklatex.com-ea162e98aa70f8d56ffba28438a9de2a_l3.png)
Et on résout les inconnues des équations de bas en haut. On résout d’abord la dernière équation :
![]()
![]()
Maintenant, nous substituons la valeur de z dans la deuxième équation pour trouver la valeur de y :
![]()
![]()
![]()
![]()
![]()
Et on fait de même avec la première équation : on substitue les valeurs des autres inconnues et on résout pour x :
![]()
![]()
![]()
![]()
La solution du système d’équations est donc :
![]()