Ici nous expliquons comment dériver une puissance (ou fonction potentielle), vous trouverez la formule de la dérivée d’une puissance, plusieurs exemples et vous pourrez même vous entraîner avec des exercices résolus étape par étape.
Formule pour la dérivée d’une puissance
La dérivée d’une puissance, ou fonction potentielle, est le produit de l’exposant de la puissance multiplié par la base élevée à l’exposant moins 1 fois la dérivée de la base.
![]()
Par conséquent, si la base est la fonction identité , pour obtenir la puissance, il suffit de multiplier la fonction par l’exposant et de soustraire une unité à l’exposant :
![]()
En effet, la dérivée de la fonction identité est égale à 1.
En résumé, pour dériver une fonction potentielle, il existe deux formules : la première qui peut toujours être utilisée et la seconde qui ne peut être appliquée que lorsque la base est un x.
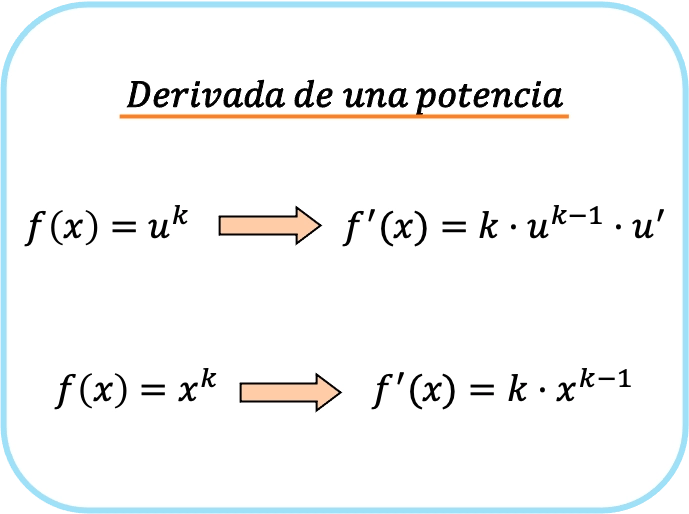
On peut facilement vérifier que la première formule présentée pour la dérivée d’une puissance est comme la seconde mais appliquant la règle de la chaîne.
A noter que ces formules ne peuvent être utilisées que lorsque la variable est la base de la puissance, si le x est au dénominateur vous devez appliquer la règle de la dérivée d’une fonction exponentielle :
➤ Voir : dérivée d’une fonction exponentielle
Exemples de dérivés de puissance
Une fois que nous aurons vu la formule de la dérivée d’une fonction potentielle, nous allons expliquer plusieurs exemples de ce type de dérivées afin que vous compreniez comment sont dérivées les puissances.
Exemple 1 : Dérivée d’une puissance de base x
![]()
Comme nous l’avons expliqué dans la section précédente, lorsque la base de la puissance est seulement un x, la formule que nous devons utiliser pour dériver la fonction est la suivante :
![]()
La dérivée de la puissance x élevée à la puissance 4 est donc :
![]()
Exemple 2 : Dérivée d’une puissance avec parenthèses
![]()
Dans cet exemple la base n’est pas la fonction identité, il faut donc utiliser la formule générale de la dérivée d’une puissance :
![]()
La fonction entre parenthèses est une fonction linéaire, donc sa dérivée est 2. Par conséquent, la dérivée de la fonction potentielle entière est :
![]()
Exemple 3 : Dérivée d’une puissance négative
![]()
Dans ce cas nous avons une fonction potentielle dont l’exposant est négatif et dont la base est un logarithme, nous utiliserons donc la formule suivante pour différencier la fonction :
![]()
Même si l’exposant de puissance est négatif, il faut aussi lui en soustraire un. La dérivée de la fonction est donc :
![]()
Si vous avez des doutes sur la résolution, vous pouvez consulter la formule de la dérivée d’une fonction logarithmique ici :
➤ Voir : dérivée d’une fonction logarithmique
Exemple 4 : Dérivée d’une puissance avec racine
![]()
La fonction dans cet exemple est une puissance au sein d’une expression rationnelle. Cependant, les radicaux peuvent être transformés en expressions potentielles, la fonction peut donc être simplifiée en la convertissant en une fonction potentielle avec un exposant fractionnaire :
![]()
Nous appliquons maintenant la formule de la dérivée d’une puissance d’une variable :
![]()
Et la dérivée est :
![]()
Vous pouvez également différencier ces types de fonctions à l’aide de la règle de dérivée racine :
➤ Voir : dérivé d’une racine
Exercices résolus sur la dérivée d’une puissance
Calculez la dérivée des puissances suivantes :
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
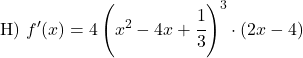
![]()