Dérivé d'une racine

Nous expliquons ici comment prendre la dérivée d’une racine (ou d’une fonction radicale). Vous trouverez la formule pour diviser les racines et des exercices résolus pas à pas de dérivées de racines.

Formule de la dérivée d’une racine

La dérivée d’une racine, ou fonction irrationnelle, est égale à la dérivée du radicande (expression sous le radical) divisée par le produit de l’indice de la racine par la même racine, en soustrayant 1 à l’exposant du radicande.

$f(x)=\sqrt[n]{u}\quad\color{orange}\bm{\longrightarrow}\color{black}\quad f'(x)=\cfrac{u'}{n\sqrt[n]{u^{n-1}}}$

Cependant, si le radicande racine n’est qu’un x, la formule se simplifie. La dérivée racine de x est donc la suivante :

$f(x)=\sqrt[n]{x}\quad\color{orange}\bm{\longrightarrow}\color{black}\quad f'(x)=\cfrac{1}{n\sqrt[n]{x^{n-1}}}$

En bref, il existe deux formules pour dériver une racine : la première qui peut toujours être utilisée et la seconde qui ne peut être utilisée que lorsque le radicande est x.

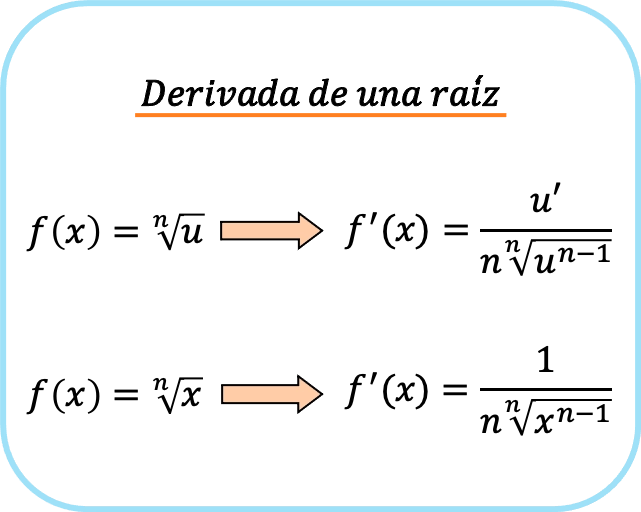
Si vous regardez bien, le terme du numérateur de la fraction est celui qui résulte de l’application de la règle de la chaîne lors de la prise de la dérivée de la racine. C’est pourquoi lorsque le radicande est x, 1 apparaît au dénominateur puisque c’est la dérivée de x.

Exemples de dérivés de racine

Étant donné la formule de la dérivée d’une fonction radicale, nous expliquons ci-dessous plusieurs exemples de ce type de dérivé afin que vous compreniez comment prendre la dérivée d’une racine.

Exemple 1 : Dérivée d’une racine carrée

Nous verrons ensuite quelle est la dérivée d’une racine carrée :

$f(x)=\sqrt{x}$

Dans ce cas, l’expression à l’intérieur de la racine est juste un x, nous pouvons donc utiliser la formule suivante :

$f(x)=\sqrt[n]{x}\quad\color{orange}\bm{\longrightarrow}\color{black}\quad f'(x)=\cfrac{1}{n\sqrt[n]{x^{n-1}}}$

Ainsi, la dérivée d’une racine carrée est égale à 1 divisé par le produit de 2 fois la racine carrée de x :

$f(x)=\sqrt{x}\quad\color{orange}\bm{\longrightarrow}\color{black}\quad f'(x)=\cfrac{1}{2\sqrt{x^{2-1}}}=\cfrac{1}{2\sqrt{x}}$

Exemple 2 : Dérivée d’une racine cubique

$f(x)=\sqrt[3]{x}$

Dans cet exemple, l’expression sous la racine est un x, nous pouvons donc appliquer la formule suivante :

$f(x)=\sqrt[n]{x}\quad\color{orange}\bm{\longrightarrow}\color{black}\quad f'(x)=\cfrac{1}{n\sqrt[n]{x^{n-1}}}$

Donc la dérivée d’une racine cubique est égale à 1 divisé par 3 fois la racine cubique de x au carré :

$f(x)=\sqrt[3]{x}\quad\color{orange}\bm{\longrightarrow}\color{black}\quad f'(x)=\cfrac{1}{3\sqrt[3]{x^{3-1}}}=\cfrac{1}{3\sqrt[3]{x^2}}$

Exemple 3 : Dérivée d’une racine quatrième

$f(x)=\sqrt[4]{7x-2}$

Maintenant, nous n’avons pas de x sous le signe radical, mais nous avons une expression algébrique plus complexe. Par conséquent, nous devons utiliser la formule générale pour la dérivée d’une racine :

$f(x)=\sqrt[n]{u}\quad\color{orange}\bm{\longrightarrow}\color{black}\quad f'(x)=\cfrac{u'}{n\sqrt[n]{u^{n-1}}}$

L’expression sous le radical est une fonction du premier degré, donc sa dérivée est 7. Ainsi, la dérivée de la fonction entière est :

$f(x)=\sqrt[4]{7x-2}\quad\color{orange}\bm{\longrightarrow}\color{black}\quad f'(x)=\cfrac{7}{4\sqrt[4]{(7x-2)^3}}$

Exemple 4 : Dérivée d’une racine dans une autre

$f(x)=\sqrt{x^2+\sqrt[3]{x^4-5}}$

Pour résoudre la dérivée de cette racine composée d’une autre racine, il faut appliquer la formule suivante :

$f(x)=\sqrt[n]{u}\quad\color{orange}\bm{\longrightarrow}\color{black}\quad f'(x)=\cfrac{u'}{n\sqrt[n]{u^{n-1}}}$

Dans ce cas, il faut utiliser la même formule deux fois de suite pour calculer la dérivée :

$\begin{aligned}f'(x)& =\cfrac{1}{2\sqrt{x^2+\sqrt[3]{x^4-5}}}\cdot\left(x^2+\sqrt[3]{x^4-5}\right)' \\[3ex]&\displaystyle =\cfrac{1}{2\sqrt{x^2+\sqrt[3]{x^4-5}}}\cdot \left(2x+\frac{1}{ 3\sqrt[3]{(x^4-5)^2}}\cdot (x^4-5)'\right)\\[3ex]&\displaystyle =\cfrac{1}{2\sqrt{x^2+\sqrt[3]{x^4-5}}}\cdot \left(2x+\frac{1}{ 3\sqrt[3]{(x^4-5)^2}}\cdot 4x^3\right)\end{aligned}$

Problèmes résolus de la dérivée d’une racine

Calculez les dérivées des racines suivantes :

$\text{A) } f(x)=\sqrt[5]{x}$

$\text{B) } f(x)=\sqrt[3]{x^4}$

$\text{C) } f(x)=\sqrt{x^2-4x+9}$

$\text{D) } f(x)=\sqrt[4]{x^9+5x^4-2x}$

$\text{E) } f(x)=\sqrt[5]{3(x^2-1)^4}$

$\text{F) } f(x)=\sqrt[6]{x^2+4(5x^3-8x)^2}$

voir solution

$\text{A) } f'(x)=\cfrac{1}{5\sqrt[5]{x^4}}$

$\text{B) } f'(x)=\cfrac{4x^3}{3\sqrt[3]{\left(x^4\right)^2}}= \cfrac{4x^3}{3\sqrt[3]{x^8}}$

$\text{C) } f'(x)=\cfrac{2x-4}{2\sqrt{x^2-4x+9}}$

$\text{D) } f'(x)=\cfrac{9x^8+20x^3-2}{4\sqrt[4]{\left(x^9+5x^4-2x\right)^3}}$

$\text{E) } f'(x)=\cfrac{3\cdot 4 \cdot (x^2-1)^3\cdot 2x}{5\sqrt[5]{\left(3\left(x^2-1\right)^4\right)^4}}=\cfrac{24x(x^2-1)^3}{5\sqrt[5]{81\left(x^2-1\right)^{16}}}$

$\text{F) } f'(x)=\cfrac{2x+2\cdot 4(5x^3-8x)\cdot (15x^2-8)}{6\sqrt[6]{\left(x^2+4(5x^3-8x)^2\right)^5}}=\cfrac{2x+8(5x^3-8x)(15x^2-8)}{6\sqrt[6]{\left(x^2+4(5x^3-8x)^2\right)^5}}$

Dérivé d’une racine

Formule de la dérivée d’une racine

Exemples de dérivés de racine

Exemple 1 : Dérivée d’une racine carrée

Exemple 2 : Dérivée d’une racine cubique

Exemple 3 : Dérivée d’une racine quatrième

Exemple 4 : Dérivée d’une racine dans une autre

Problèmes résolus de la dérivée d’une racine

Leave a Comment Cancel Reply