Dérivée d'arcsinus hyperbolique

Vous trouverez ici quelle est la dérivée de l’arcsinus hyperbolique (formule). De plus, vous pourrez voir plusieurs exercices résolus sur les dérivées de l’arcsinus hyperbolique d’une fonction. Enfin, nous vous montrons la formule de la dérivée de ce type de fonction trigonométrique.

Formule dérivée arcsinus hyperbolique

La dérivée de l’arcsinus hyperbolique de x est un sur la racine carrée de x au carré plus 1.

$f(x)=\text{arcsenh}(x) \quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=\cfrac{1}{\sqrt{x^2+1}}$

Ainsi, la dérivée de l’arc sinus hyperbolique d’une fonction est égale au quotient de la dérivée de cette fonction divisé par la racine carrée de cette fonction au carré plus un.

$f(x)=\text{arcsenh}(u) \quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=\cfrac{u'}{\sqrt{u^2+1}}$

La deuxième formule est comme la première mais en appliquant la règle de la chaîne. C’est-à-dire qu’avec la première formule, seul l’arc sinus hyperbolique de xy peut être dérivé, alors qu’avec la seconde formule, l’arc sinus hyperbolique de n’importe quelle fonction peut être dérivé.

Gardez à l’esprit que l’arcsinus hyperbolique est la fonction inverse du sinus hyperbolique, dont vous pouvez voir la dérivée ici :

➤ Voir : formule de la dérivée du sinus hyperbolique

Exemples de la dérivée de l’arcsinus hyperbolique

Exemple 1

$f(x)=\text{arcsenh}(3x)$

Pour résoudre la dérivée de la fonction arc sinus, on utilise la formule vue ci-dessus :

$f(x)=\text{arcsenh}(u) \quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=\cfrac{u'}{\sqrt{u^2+1}}$

La dérivée de 3x est 3, donc un 3 va au numérateur. Et au dénominateur, nous devons simplement mettre la racine carrée de 3x au carré plus 1 :

$f(x)=\text{arcsenh}(3x) \quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=\cfrac{3}{\sqrt{(3x)^2+1}}=\cfrac{3}{\sqrt{9x^2+1}}$

Exemple 2

$f(x)=\text{arcsenh}(x^3)$

Pour dériver l’arcsinus hyperbolique de la fonction x au cube, il faut appliquer la même formule :

$f(x)=\text{arcsenh}(u) \quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=\cfrac{u'}{\sqrt{u^2+1}}$

La dérivée de x au cube est 3x ² , donc la dérivée de l’arcsinus hyperbolique de x élevé à 3 sera :

$f(x)=\text{arcsenh}(x^3) \quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=\cfrac{3x^2}{\sqrt{\left(x^3\right)^2+1}}=\cfrac{3x^2}{\sqrt{x^6+1}}$

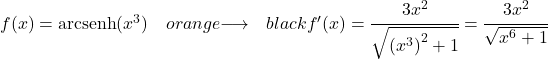
Preuve de la dérivée de l’arc sinus hyperbolique

Nous allons démontrer la formule de la dérivée de l’arcsinus hyperbolique :

$y=\text{arcsenh}(x)$

Tout d’abord, on transforme l’arcsinus hyperbolique en sinus hyperbolique :

$x=\text{senh}(y)$

On déduit des deux côtés de l’égalité :

$1=\text{cosh}(y)\cdot y'$

Nous vous dédouanons :

$y'=\cfrac{1}{\text{cosh}(y)}$

Ensuite, on applique l’identité trigonométrique qui relie le sinus hyperbolique et le cosinus hyperbolique :

$\text{cosh}^2(y)-\text{senh}^2(y)=1 \ \longrightarrow \ \text{cosh}(y)=\sqrt{1+\text{senh}^2(y)}$

$y'=\cfrac{1}{\sqrt{1+\text{senh}^2(y)}}$

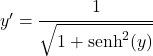
Mais ci-dessus nous avons déduit que x correspond au sinus hyperbolique de y, de sorte que l’équation reste :

$y'=\cfrac{1}{\sqrt{1+x^2}}$

Comme vous pouvez le voir, en appliquant ces étapes, nous avons obtenu la formule de la dérivée de l’arc sinus hyperbolique, c’est pourquoi elle est prouvée.

Dérivée d’arcsinus hyperbolique

Formule dérivée arcsinus hyperbolique

Exemples de la dérivée de l’arcsinus hyperbolique

Exemple 1

Exemple 2

Preuve de la dérivée de l’arc sinus hyperbolique

Articles Similaires

Leave a Comment Cancel Reply