▷ Différentiabilité d'une fonction (théorie et exercices résolus)

Dans cet article, vous apprendrez comment étudier la différentiabilité d’une fonction, c’est-à-dire savoir si une fonction est différentiable ou non. De plus, nous verrons la relation entre différentiabilité et continuité d’une fonction. Et enfin, nous étudierons la différentiabilité d’une fonction par morceaux.

Différentiabilité et continuité d’une fonction

La continuité et la différentiabilité d’une fonction en un point sont liées comme suit :

Si une fonction est différentiable en un point, la fonction est continue en ce point.
Si une fonction n’est pas continue en un point, elle n’est pas non plus dérivable en ce point.

Cependant, l’inverse de ce théorème est faux : ce n’est pas parce qu’une fonction est continue en un point qu’elle est toujours dérivable en ce point.

Vous pouvez également voir si une fonction est différentiable ou non en un point à partir de sa représentation graphique :

S’il s’agit d’un point lisse, la fonction est dérivable en ce point.
S’il s’agit d’un point angulaire, la fonction est continue mais non dérivable en ce point.

Point de lissage à x=0 :
fonction continue et différentiable à ce stade.

Point angulaire en x=2 :
fonction continue mais non différenciable à ce stade.

Différentiabilité d’une fonction par morceaux

Une fois que nous connaîtrons la relation entre continuité et différentiabilité d’une fonction, nous allons voir comment étudier la différentiabilité d’une fonction définie par morceaux.

Vous pouvez savoir si une fonction par morceaux est différentiable en un point en calculant les dérivées latérales à ce point :

Si les dérivées latérales en un point ne sont pas égales, la fonction n’est pas dérivable en ce point :

$f'(x_o^-) \neq f'(x_o^+) \ \longrightarrow$ Il n’est pas déductible dans $x_o$

Si les dérivées latérales en un point coïncident, la fonction est dérivable en ce point :

$f'(x_o^-) = f'(x_o^+) \ \longrightarrow$ Oui, c’est dérivable dans $x_o$

Remarque : Pour qu’une fonction soit dérivable en un point, la fonction doit être continue en ce point. Par conséquent, avant de calculer les dérivées latérales, nous devons nous assurer que la fonction est continue en ce point. Si vous ne savez pas comment la continuité est étudiée en un point, vous pouvez voir comment cela se fait dans le lien suivant :

➤ Voir : continuité d’une fonction en un point

Voyons maintenant un exemple de comment calculer la dérivée d’une fonction définie par morceaux en un point :

Étudiez la continuité et la différentiabilité de la fonction suivante définie par morceaux au point x=2 :

$\displaystyle f(x)= \left\{ \begin{array}{lcl} 3x^2-6x & \text{si} & x<2 \\[2ex] 6\ln (x-1) & \text{si} & x\geq 2 \end{array} \right.$

Les fonctions des deux pièces sont continues dans leurs intervalles respectifs, cependant il faut voir si la fonction est continue au point critique x=2. Pour ce faire, on résout les limites latérales de la fonction au point :

$\lim\limits_{x\to 2^-} f(x) = \lim\limits_{x\to 2^-} \bigl(3x^2-6x\bigr) = 3\cdot2^2-6\cdot2=12-12=\bm{0}$

$\lim\limits_{x\to 2^+} f(x) = \lim\limits_{x\to 2^+} 6\ln (x-1) = 6\ln (2-1)=6 \ln 1=6 \cdot 0= \bm{0}$

Les limites latérales au point critique nous ont donné le même résultat, donc la fonction est continue au point x=2.

Une fois que nous savons que la fonction est continue en x=2, nous allons étudier la différentiabilité de la fonction à ce point. Pour ce faire, on calcule les dérivées latérales de la fonction définie en morceaux :

$\displaystyle f'(x)= \left\{ \begin{array}{lcl} 6x-6 & \text{si} & x<2 \\[2ex] \cfrac{6}{x-1} & \text{si} & x\geq 2 \end{array} \right.$

Nous évaluons maintenant chaque dérivée latérale au point critique :

$f'(2^-)=6\cdot2-6=12-6 = \bm{6}$

$f'(2^+)=\cfrac{6}{2-1} = \cfrac{6}{1} = \bm{6}$

Les deux dérivées latérales nous ont donné le même résultat, donc la fonction est différentiable en x=2 et la valeur de la dérivée est 6 :

$f'(2^-) = f'(2^+) = 6 \ \longrightarrow \ \bm{f'(2) = 6}$

En revanche, si les dérivées latérales nous avaient donné un résultat différent, cela voudrait dire que la fonction n’est pas dérivable en x=2. Autrement dit, la dérivée n’existerait pas à ce stade.

Pour finir, dites-vous simplement que cette procédure est également valable pour étudier la différentiabilité d’une fonction à valeur absolue, puisque les fonctions à valeurs absolues peuvent également être définies par morceaux. Vous pouvez voir comment convertir une fonction de valeur absolue en morceaux ici :

➤ Voir : comment définir par morceaux une fonction avec une valeur absolue

Exercices résolus sur la différentiabilité d’une fonction

Exercice 1

Étudiez la continuité et la différentiabilité de la fonction par morceaux suivante :

$\displaystyle f(x)= \left\{ \begin{array}{lcl} x^3-4x^2 + 5 & \text{si} & x<1 \\[2ex] -x^2+3x & \text{si} & x\geq 1 \end{array} \right.$

Voir la solution

Les fonctions des deux pièces sont continues, mais il faut voir si la fonction est continue au point critique x=1. Pour ce faire on résout les limites latérales de la fonction au point :

$\lim\limits_{x\to 1^-} f(x) = \lim\limits_{x\to 1^-} \bigl(x^3-4x^2 + 5\bigr)=1^3-4\cdot 1^2 + 5=2$

$\lim\limits_{x\to 1^+} f(x) = \lim\limits_{x\to 1^+} \bigl( -x^2+3x \bigr)=-1^2+3\cdot 1=2$

Les deux limites latérales au point critique donnent le même résultat, donc la fonction est continue en x=1.

Une fois que nous savons que la fonction est continue au point critique, nous étudierons si elle est dérivable au même point. On calcule donc les dérivées latérales :

$\displaystyle f'(x)= \left\{ \begin{array}{lcl} 3x^2-8x & \text{si} & x<1 \\[2ex] -2x+3 & \text{si} & x\geq 1 \end{array} \right.$

Et nous évaluons les deux dérivées latérales à x=1 ;

$f'(1^-)=3\cdot1^2-8\cdot 1=3-8=-5$

$f'(1^+)=-2\cdot 1+3=-2+3 =1$

Les dérivées latérales ne coïncident pas au point x=1 donc la fonction n’est pas dérivable à ce point.

$f'(1^-) \neq f'(1^+) \ \longrightarrow \ \cancel{\exists} \ f'(1)$

Exercice 2

Analyser la dérivabilité et la continuité de la fonction suivante définie dans les sections :

$\displaystyle f(x)= \left\{ \begin{array}{lcl} \sqrt{4x} & \text{si} & x\leq 1 \\[2ex] 2+\ln x & \text{si} & x> 1 \end{array} \right.$

Voir la solution

Les fonctions des deux sections sont continues dans leurs intervalles, mais il faut aussi savoir si la fonction est continue au point critique de changement de définition x=1. Nous définissons donc les limites latérales de la fonction à ce point :

$\lim\limits_{x\to 1^-} f(x) = \lim\limits_{x\to 1^-} \sqrt{4x} = \sqrt{4\cdot 1} = \sqrt{4}=2$

$\lim\limits_{x\to 1^+} f(x) = \lim\limits_{x\to 1^+} \bigl( 2+\ln x \bigr) = 2 + \ln (1) = 2+0 =2$

Les deux limites latérales au point critique donnent le même résultat, donc la fonction est continue en x=1.

Et maintenant nous étudions si la fonction est différentiable en ce point en calculant les dérivées latérales :

$\displaystyle f'(x)= \left\{ \begin{array}{lcl} \cfrac{4}{2\sqrt{4x}} & \text{si} & x<1 \\[4ex] \cfrac{1}{x} & \text{si} & x\geq 1 \end{array} \right.$

Nous évaluons les deux dérivées latérales à x=1 :

$f'(1^-)=\cfrac{4}{2\sqrt{4\cdot1}}=\cfrac{4}{2\sqrt{4}}=\cfrac{4}{2\cdot 2}=\cfrac{4}{4}=1$

$f'(1^+)=\cfrac{1}{1}=1$

Les dérivées latérales sont égales, donc la fonction est différentiable en x=1 et la valeur de la dérivée est 1.

$f'(1^-) = f'(1^+) = 1 \ \longrightarrow \ \bm{f'(1) = 1}$

Exercice 3

Déterminez si la fonction par morceaux suivante est continue et différentiable sur l’ensemble de son domaine :

*** QuickLaTeX cannot compile formula:
\displaystyle f(x)= \left\{ \begin{array}{lcl} x^2+2x+1 & \text{si} &  x\leq -1 \\[2ex] 2x+2 & \text{si} & -1<div class="wp-block-otfm-box-spoiler-start otfm-sp__wrapper otfm-sp__box js-otfm-sp-box__closed otfm-sp__E6F9EF" role="button" tabindex="0" aria-expanded="false" data-otfm-spc="#E6F9EF" style="text-align:center"><div class="otfm-sp__title"> <strong>Voir la solution</strong></div></div> Les fonctions des trois pièces sont continues, mais nous devons encore vérifier si la fonction est continue aux points critiques. On vérifie donc d'abord la continuité de la fonction au point x=-1 en résolvant les limites latérales en ce point : 

*** Error message:
Missing $ inserted.
leading text: \displaystyle
Missing { inserted.
leading text: ...="wp-block-otfm-box-spoiler-start otfm-sp__
Missing { inserted.
leading text: ...ox-spoiler-start otfm-sp__wrapper otfm-sp__
Missing { inserted.
leading text: ...m-sp__wrapper otfm-sp__box js-otfm-sp-box__
Missing { inserted.
leading text: ...fm-sp__box js-otfm-sp-box__closed otfm-sp__
You can't use `macro parameter character #' in math mode.
leading text: ...="0" aria-expanded="false" data-otfm-spc="#
Missing { inserted.
leading text: ...e="text-align:center"><div class="otfm-sp__
Please use \mathaccent for accents in math mode.
leading text: ...g></div></div> Les fonctions des trois piè
Please use \mathaccent for accents in math mode.
leading text: ...sont continues, mais nous devons encore vé

\lim\limits_{x\to -1^-} f(x) = \lim\limits_{x\to -1^-} \bigl(x^2+2x+1\bigr) = (-1)^2+2(-1)+1 =0 \lim\limits_{x\to -1^+} f(x) = \lim\limits_{x\to -1^+} \bigl(2x+2\bigr) = 2(-1)+2=0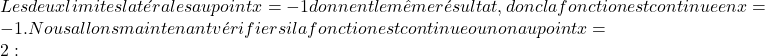 $Les deux limites latérales au point x=-1 donnent le même résultat, donc la fonction est continue en x=-1. Nous allons maintenant vérifier si la fonction est continue ou non au point x=2 :$ \lim\limits_{x\to 2^-} f(x) = \lim\limits_{x\to 2^-} \bigl(2x+2\bigr) = 2\cdot 2+2=4+2=6 \lim\limits_{x\to 2^+} f(x) = \lim\limits_{x\to 2^+} \bigl( -x^2+8x\bigr) = -2^2+8\cdot 2 = -4+16=12 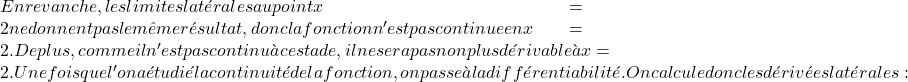$En revanche, les limites latérales au point x=2 ne donnent pas le même résultat, donc la fonction n'est pas continue en x=2. De plus, comme il n'est pas continu à ce stade, il ne sera pas non plus dérivable à x=2. Une fois que l'on a étudié la continuité de la fonction, on passe à la différentiabilité. On calcule donc les dérivées latérales :$ \displaystyle f'(x)= \left\{ \begin{array}{lcl} 2x+2 & \text{si} & x\leq -1 \\[2ex] 2 & \text{si} & -1

Nous savons déjà que la fonction n’est pas dérivable en x=2, il suffit donc d’étudier si la fonction est dérivable en x=-1. Pour ce faire, nous évaluons les deux dérivées latérales au point :

$f'(-1^-)=2(-1)+2 = -2+2=0$

$f'(-1^+)=2$

Les dérivées latérales ne coïncident pas au point x=-1, donc la fonction n’est pas dérivable à ce point.

$f'(-1^-) \neq f'(-1^+) \ \longrightarrow \ \cancel{\exists} \ f'(-1)$

Exercice 4

Calculez la valeur des paramètres a et b pour que la fonction par morceaux suivante soit continue et différentiable dans tout son domaine :

$\displaystyle f(x)= \left\{ \begin{array}{lcl} 2e^{x-3} + a & \text{si} & x< 3 \\[2ex](x-b)^2 & \text{si} & x\geq 3 \end{array} \right.$

Voir la solution

Quelles que soient les valeurs des inconnues, la fonction est continue et différentiable en tous points sauf en x=3, où il faut vérifier sa continuité et sa différentiabilité.

Pour que la fonction soit continue en un point, les deux limites latérales en ce point doivent coïncider. Par conséquent, nous évaluons les limites latérales au point critique :

$\lim\limits_{x\to 3^-} f(x) = \lim\limits_{x\to 3^-} \bigl(2e^{x-3}+a\bigr) = 2e^{3-3}+a = 2 \cdot e^0+a =2\cdot 1 +a = 2+a$

$\lim\limits_{x\to 3^+} f(x) = \lim\limits_{x\to 3^+} (x-b)^2 = (3-b)^2$

Il faut donc que les deux valeurs obtenues à partir des limites latérales soient égales pour que la fonction soit continue :

$2+a = (3-b)^2$

Nous allons maintenant analyser la différentiabilité au point x=3. On retrouve les dérivées latérales :

$\displaystyle f'(x)= \left\{ \begin{array}{lcl} 2e^{x-3} & \text{si} & x< 3 \\[2ex]2(x-b) & \text{si} & x\geq 3 \end{array} \right.$

Et nous évaluons les deux dérivées latérales au point critique :

$f'(3^-)= 2e^{3-3} = 2e^0 = 2\cdot 1 = 2$

$f'(3^+)=2(3-b) = 6 - 2b$

Par conséquent, pour que la fonction soit dérivable en x=3, les valeurs obtenues à partir des dérivées latérales doivent être égales :

$2=6-2b$

Et en résolvant cette équation nous pouvons trouver la valeur de b :

$2b=6-2$

$2b=4$

$b=\cfrac{4}{2} =\bm{2}$

Enfin, une fois que l’on connaît la valeur du paramètre b, on peut calculer la valeur du paramètre a en résolvant l’équation que l’on a obtenue précédemment dans les limites latérales :

$2+a = (3-b)^2$

$2+a = (3-2)^2$

$2+a =1$

$a =1-2$

$\bm{a =-1}$

Différentiabilité et continuité d’une fonction

Différentiabilité d’une fonction par morceaux

Exercices résolus sur la différentiabilité d’une fonction

Exercice 1

Exercice 2

Exercice 3

Exercice 4

Leave a Comment Cancel Reply