Fonctions à valeur absolue -

Cette page explique ce qu’est une fonction de valeur absolue. Vous découvrirez également comment définir une fonction de valeur absolue par morceaux et comment représenter ces types de fonctions sur un graphique. De plus, vous le verrez avec des exemples de fonctions à valeur absolue et vous pourrez vous entraîner avec des exercices et des problèmes résolus étape par étape.

Que sont les fonctions à valeur absolue ?

La définition d’une fonction à valeur absolue est la suivante :

La valeur absolue d’une fonction transforme toutes ses images en images positives. Par conséquent, le chemin d’une fonction absolue ne peut jamais avoir de valeurs négatives.

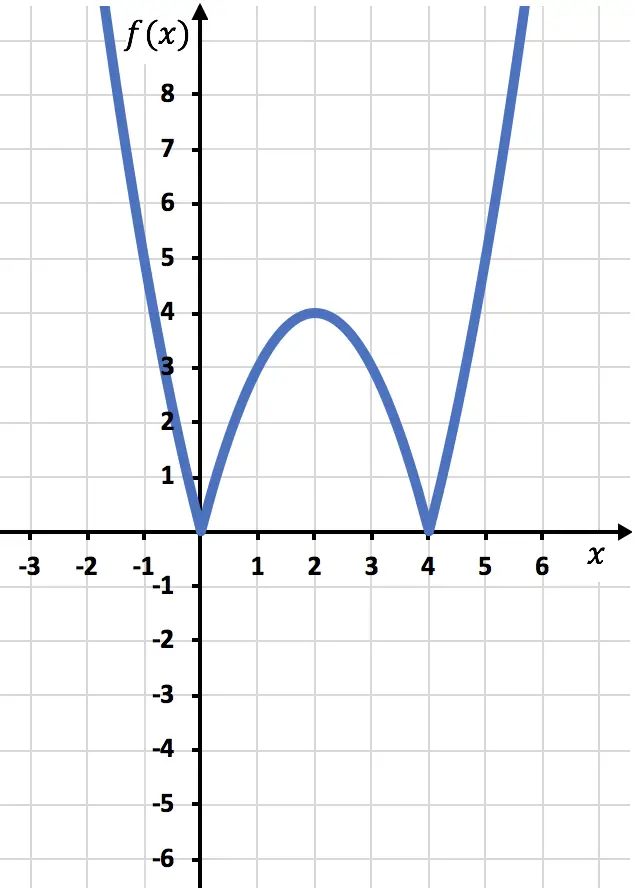
La fonction suivante est un exemple de fonction valeur absolue :

$f(x)=\lvert 5x \rvert$

Si lors de l’évaluation de la fonction en un point nous obtenons un résultat positif, il reste positif :

$f(1)=\lvert 5\cdot 1 \rvert =\lvert 5 \rvert = 5$

En revanche, si le résultat est négatif il devient positif :

$f(-1)=\lvert 5\cdot (-1) \rvert =\lvert -5 \rvert = 5$

Les fonctions à valeur absolue sont généralement données au lycée, car leurs caractéristiques les rendent un peu difficiles à comprendre.

Comment définir par morceaux une fonction avec une valeur absolue

Une fonction à valeur absolue peut être exprimée sous la forme d’une fonction par morceaux. Pour ce faire, il faut changer le signe de la fonction sur les intervalles qui est négatif.

Voyons un exemple de la façon de passer d’une fonction de valeur absolue à une fonction par morceaux :

Exprimez la fonction suivante avec une valeur absolue sous la forme d’une fonction par morceaux :

$f(x) = \lvert 4 - x^2 \rvert$

La première chose que nous devons faire est de déterminer quand la fonction est négative. Pour ce faire, nous fixons l’expression algébrique en valeur absolue égale à 0 et résolvons l’équation :

$4-x^2=0$

$4 = x^2$

$\sqrt{4}=\sqrt{x^2}$

$\pm 2 = x$

$x=+2 \qquad x=-2$

Nous représentons maintenant les valeurs obtenues sur la ligne :

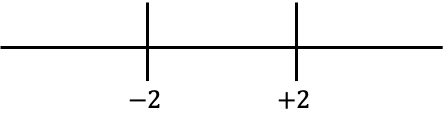
Et nous regardons quel signe a la fonction sans la valeur absolue dans chaque intervalle de la ligne :

$x<-2$

On prend tout point inférieur à -2, par exemple

$x=-3:$

$4-(-3)^2$

$-5$

Négatif

$-2 < x < 2$

On prend n’importe quel point entre -2 et +2, par exemple

$x=0:$

$4-0^2$

$+4$

Positif

$x>2$

On prend par exemple tout point supérieur à 2

$x=3:$

$4-3^2$

$-5$

Négatif

Comme nous l’avons vu, la fonction sans la valeur absolue serait négative sur les intervalles

$x<-2$ et $x>2.$ Par conséquent, nous devons exprimer la fonction en tirets en changeant son signe dans ces intervalles :

$\displaystyle f(x)= \lvert 4 - x^2 \rvert = \left\{ \begin{array}{lcl} -(4-x^2) & \text{si} & x<-2 \\[2ex] 4-x^2 & \text{si} & -2 \le x \le 2 \\[2ex] -(4-x^2) & \text{si} & x>2 \end{array} \right.$

$\displaystyle f(x)= \lvert 4 - x^2 \rvert = \left\{ \begin{array}{lcl} -4+x^2 & \text{si} & x<-2 \\[2ex] 4-x^2 & \text{si} & -2 \le x \le 2 \\[2ex] -4+x^2 & \text{si} & x>2 \end{array} \right.$

Notez que dans certains intervalles, vous devez inclure l’égalité. Par exemple, ici nous l’avons mis dans le deuxième intervalle

$-2 \le x \le 2$ . Mais vous pouvez le placer dans n’importe quel intervalle de votre choix à condition qu’il y ait une égalité dans tous les points critiques. Autrement dit, ce serait la même chose si nous avions défini la fonction comme suit :

$\displaystyle f(x)= \lvert 4 - x^2 \rvert = \left\{ \begin{array}{lcl} -4+x^2 & \text{si} & x\le-2 \\[2ex] 4-x^2 & \text{si} & -2 < x < 2 \\[2ex] -4+x^2 & \text{si} & x\ge 2 \end{array} \right.$

Comment représenter une fonction avec une valeur absolue

Pour représenter une fonction avec une valeur absolue sur un graphique, nous devons suivre les étapes décrites ci-dessous :

Représentez la fonction comme si elle n’avait pas la valeur absolue.
Dans les intervalles dans lesquels la fonction est négative, c’est-à-dire qu’elle se trouve en dessous de l’axe X, dessinez la fonction symétrique.
Supprimez la partie de la fonction qui se trouve en dessous de l’axe X.

Voyons un exemple de la façon de représenter graphiquement une fonction avec une valeur absolue

Représentez graphiquement la fonction suivante en valeur absolue :

$f(x) = \lvert -x+2 \rvert$

Pour représenter une fonction de valeur absolue, nous devons d’abord représenter la fonction sans la valeur absolue. On fait donc le tableau des valeurs des fonctions sans la valeur absolue :

$f(x)=-x+2$

$x= 0 \ \longrightarrow \ f(0) = -0+2=2$

$x= 1 \ \longrightarrow \ f(1) = -1+2=1$

$x= 2 \ \longrightarrow \ f(2) = -2+2=0$

$\begin{array}{c|c} x & f(x) \\ \hline 0 & 2 \\ 1 & 1 \\ 2 & 0 \end{array}$

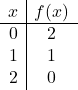
Nous représentons les points sur un graphique et traçons la ligne comme s’il s’agissait d’une fonction normale :

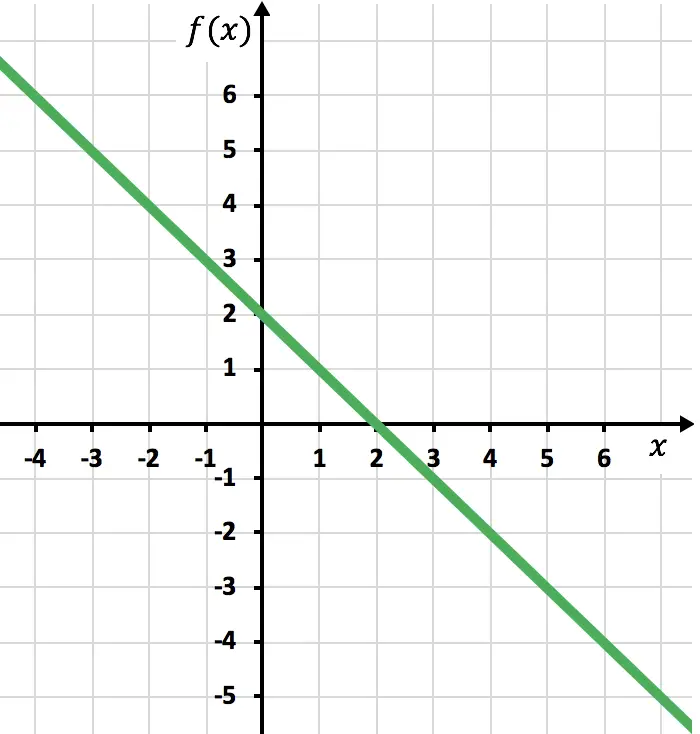
Nous devons maintenant dessiner la fonction symétrique là où la fonction est négative, c’est-à-dire là où elle se trouve en dessous de l’axe des x. Par conséquent, nous inversons la fonction à partir de x=2 :

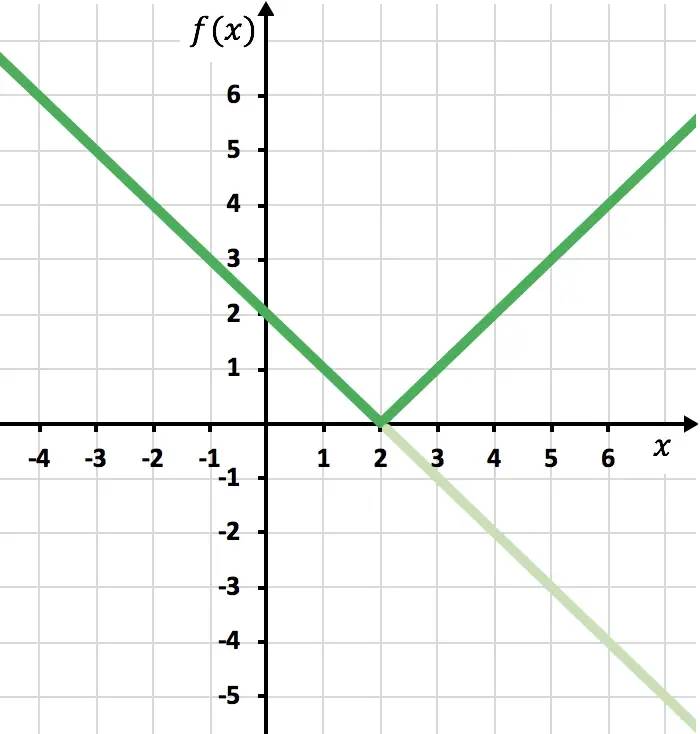
comment représenter une fonction avec une valeur absolue

Et enfin on élimine la trace de la fonction qui se trouve en dessous de l’axe X :

comment tracer graphiquement une fonction avec une valeur absolue

Et de cette façon, nous avons déjà représenté la fonction avec une valeur absolue. Comme vous l’avez vu, la seule chose qui change c’est qu’il faut inverser la partie de la fonction qui se trouve en dessous de l’axe OX. Par conséquent, le graphique de toute fonction avec une valeur absolue se situera toujours du côté de l’axe semi-Y positif.

D’un autre côté, pour revoir les concepts, à partir du graphique, on peut déduire que le domaine de la fonction de valeur absolue précédente est entièrement constitué de nombres réels. En revanche, la plage ou la plage de ladite fonction avec une valeur absolue est composée uniquement de nombres positifs et de zéro.

Exercices résolus sur les fonctions à valeur absolue

Exercice 1

Exprimez la fonction suivante avec une valeur absolue sous la forme d’une fonction par morceaux :

$f(x)= \lvert -x+3 \rvert$

Voir la solution

Tout d’abord, il faut regarder quand la fonction est négative. Pour ce faire, nous fixons la valeur absolue égale à zéro et résolvons l’équation :

$-x+3=0$

$x=3$

Nous représentons la valeur trouvée sur la ligne :

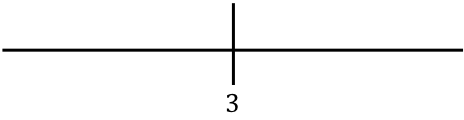
Maintenant, nous évaluons un point de chaque intervalle de la fonction sans la valeur absolue pour savoir quel signe la fonction a réellement dans chaque section de la ligne :

$x<3$

On prend par exemple tout point inférieur à 3

$x=0:$

$-0+3$

$+3$

Positif

$x>3$

On prend par exemple n’importe quel point supérieur à 3

$x=4:$

$-4+3$

$-1$

Négatif

La fonction sans la valeur absolue serait négative dans l’intervalle x>3. Il faut donc exprimer la fonction en tirets en changeant son signe dans cet intervalle :

$\displaystyle f(x)= \lvert -x+3 \rvert = \left\{ \begin{array}{lcl} -x+3 & \text{si} & x<3 \\[2ex] -(-x+3) & \text{si} & x\ge 3 \end{array} \right.$

$\displaystyle f(x)= \lvert -x+3 \rvert = \left\{ \begin{array}{lcl} -x+3 & \text{si} & x<3 \\[2ex] x-3 & \text{si} & x\ge 3 \end{array} \right.$

Exercice 2

Trouvez l’expression sous forme de morceaux de la fonction suivante avec une valeur absolue :

$f(x)= \lvert 3x^2-75 \rvert$

Voir la solution

La première chose que nous devons faire est de déterminer quand la fonction est négative. Pour ce faire, nous devons mettre l’argument valeur absolue égal à zéro et résoudre l’équation :

$3x^2-75 =0$

$3x^2=75$

$x^2=\cfrac{75}{3}$

$x^2=25$

$x= \pm 5$

On représente maintenant les racines de la fonction obtenue sur la droite :

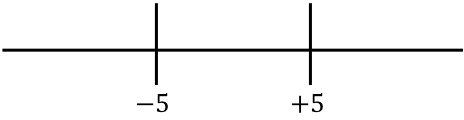
Et nous regardons quel signe a la fonction sans la valeur absolue dans chaque intervalle de la ligne :

$x<-5$

On prend par exemple tout point inférieur à -5

$x=-6:$

$3(-6)^2-75$

$108-75$

$+33$

Positif

$-5 < x < 5$

On prend n’importe quel point entre -5 et +5, par exemple

$x=0:$

$3(0)^2-75$

$0-75$

$-75$

Négatif

$x>5$

On prend par exemple n’importe quel point supérieur à 5

$x=6:$

$3(6)^2-75$

$108-75$

$+33$

Positif

Par conséquent, la fonction sans la valeur absolue ne serait négative que dans l’intervalle -5<x<5. Par conséquent, nous devons exprimer la fonction en parties en changeant uniquement le signe de cet intervalle :

$\displaystyle f(x)= \lvert 3x^2-75 \rvert = \left\{ \begin{array}{lcl} 3x^2-75 & \text{si} & x<-5 \\[2ex] -(3x^2-75) & \text{si} & -5 \le x \le 5 \\[2ex] 3x^2-75 & \text{si} & x>5 \end{array} \right.$

$\displaystyle f(x)= \lvert 3x^2-75 \rvert = \left\{ \begin{array}{lcl} 3x^2-75 & \text{si} & x<-5 \\[2ex] -3x^2+75 & \text{si} & -5 \le x \le 5 \\[2ex] 3x^2-75 & \text{si} & x>5 \end{array} \right.$

Exercice 3

Faites la représentation graphique de la fonction suivante en valeur absolue :

$f(x)= \lvert 2x-6 \rvert$

Voir la solution

Pour représenter une fonction avec une valeur absolue, il faut d’abord représenter la fonction sans la valeur absolue :

$f(x)= 2x+6$

C’est une fonction affine, il faut donc construire un tableau de valeurs pour la représenter graphiquement :

$x=0 \longrightarrow f(0)=2\cdot 0-6=-6$

$x=1 \longrightarrow f(1)=2\cdot 1-6=-4$

$x=2 \longrightarrow f(2)=2\cdot 2-6=-2$

$\begin{array}{c|c} x & f(x) \\ \hline 0 & -6 \\ 1 & -4 \\ 2 & -2 \end{array}$

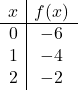
Nous représentons les points sur le graphique et traçons la ligne :

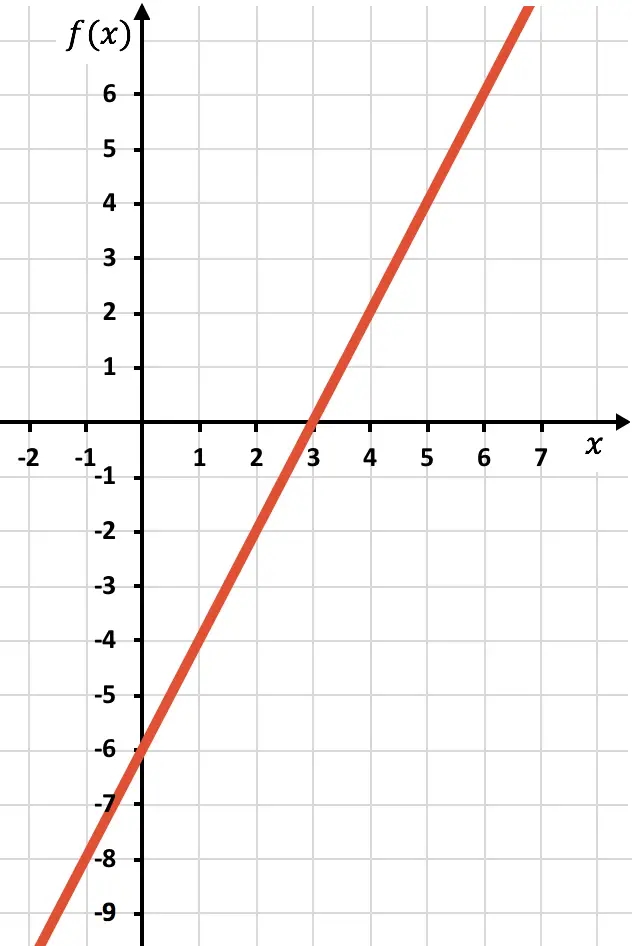
exercice résolu 3 fonction de valeur absolue 1

Nous devons maintenant dessiner la fonction symétrique là où la fonction est négative, c’est-à-dire là où elle se trouve en dessous de l’axe X. Par conséquent, nous inversons la fonction de x=3 vers l’envers :

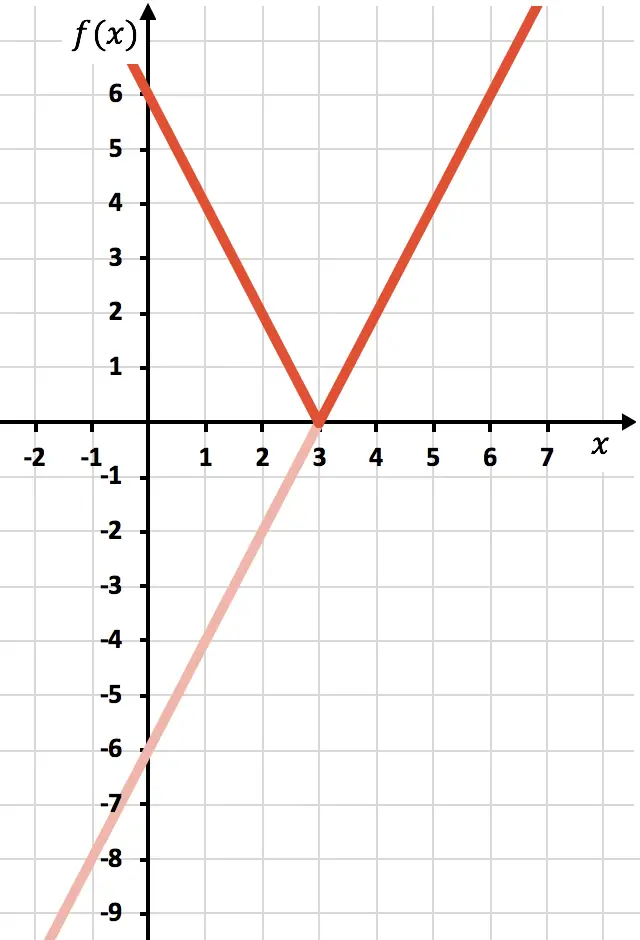
exercice résolu 3 fonction de valeur absolue 2

Et enfin, on élimine la partie de la fonction qui se trouve en dessous de l’axe X :

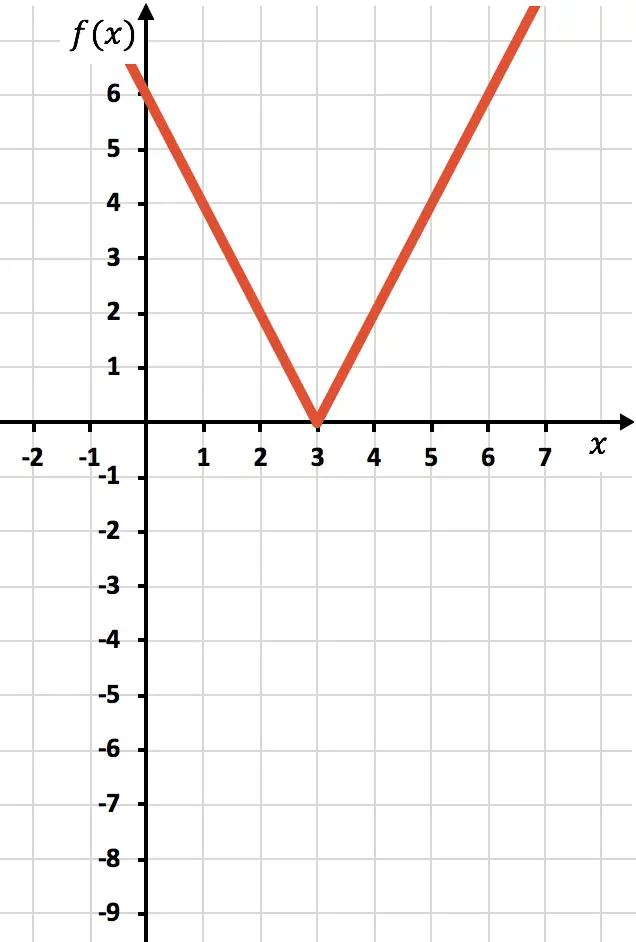
exercices résolus sur des fonctions à valeur absolue

Exercice 4

Représentez graphiquement la fonction suivante en valeur absolue :

$f(x)= \lvert x^2-4x \rvert$

Voir la solution

Pour représenter une fonction avec une valeur absolue, nous devons d’abord dessiner la fonction sans la valeur absolue.

$f(x)= x^2-4x$

Il s’agit d’une fonction quadratique. Par conséquent, pour la représenter, nous devons calculer la coordonnée X du sommet de la parabole avec sa formule :

$x = \cfrac{-b}{2a} = \cfrac{-(-4)}{2\cdot 1} = \cfrac{+4}{2} = 2$

Maintenant, nous créons une table de valeurs. Pour ce faire, nous calculons la valeur de

$f(x)$ au sommet et autour du sommet :

$x= 2 \ \longrightarrow \ f(2)=2^2-4\cdot 2 = -4$

$x= 1 \ \longrightarrow \ f(1)=1^2-4\cdot 1 = -3$

$x= 3 \ \longrightarrow \ f(3)=3^2-4\cdot 3 = -3$

$x= 0 \ \longrightarrow \ f(0)=0^2-4\cdot 0 = 0 -0 = 0$

$x= 4 \ \longrightarrow \ f(4)=4^2-4\cdot 4 = 0$

$\begin{array}{c|c} x & f(x) \\ \hline 2 & -4 \\ 1 & -3 \\ 3 & -3 \\ 0 & 0 \\ 4 & 0 \end{array}$

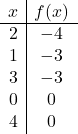
Nous représentons les points sur le graphique et dessinons la parabole :

Nous devons maintenant traduire la fonction par symétrie là où elle est négative, c’est-à-dire là où elle est en dessous de l’axe OX. Par conséquent, nous inversons la fonction de x=0 à x=4 :

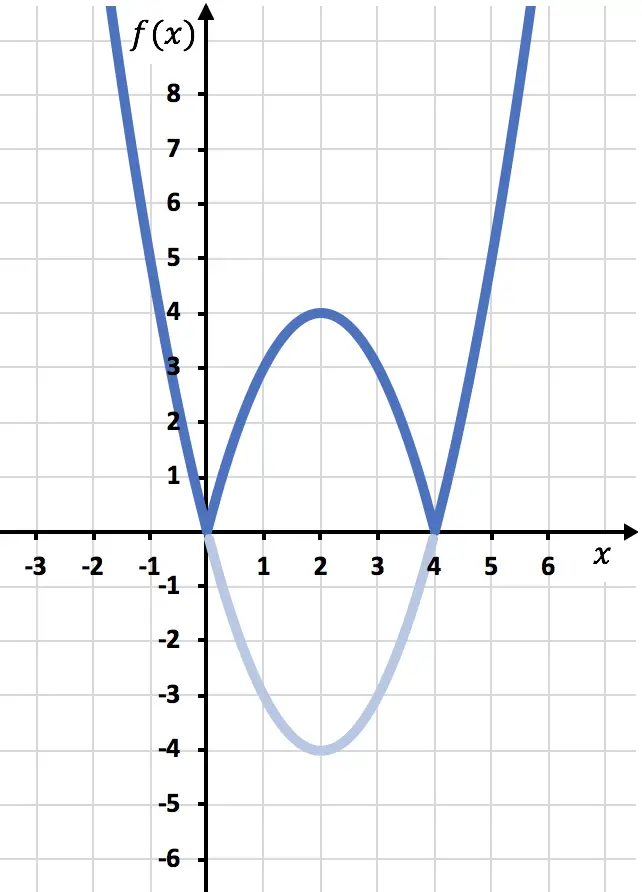
Et enfin on supprime la partie de la fonction qui se trouve en dessous de l’axe X :

Que sont les fonctions à valeur absolue ?

Comment définir par morceaux une fonction avec une valeur absolue

Comment représenter une fonction avec une valeur absolue

Exercices résolus sur les fonctions à valeur absolue

Exercice 1

Exercice 2

Exercice 3

Exercice 4

Leave a Comment Cancel Reply