Vous trouverez ici quelles sont les asymptotes verticales d’une fonction (avec des exemples). Nous vous expliquons également comment trouver les asymptotes verticales d’une fonction et, en plus, vous pourrez vous entraîner avec des exercices résolus pas à pas.
Qu’est-ce qu’une asymptote verticale ?
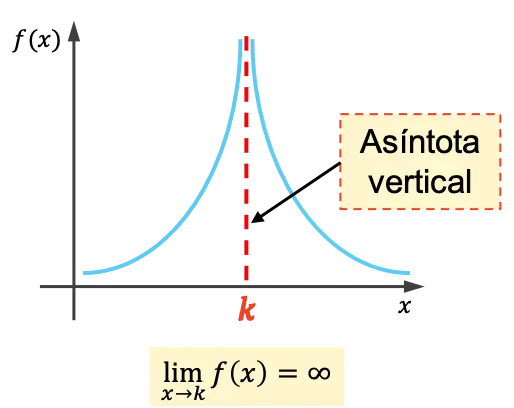
Une asymptote verticale d’une fonction est une droite verticale dont son graphe se rapproche indéfiniment sans jamais la croiser. Par conséquent, l’équation d’une asymptote verticale est x=k , où k est la valeur de l’asymptote verticale.
Autrement dit, k est une asymptote verticale si la limite de la fonction lorsque x s’approche de k est infinie.
Comment calculer l’asymptote verticale d’une fonction
Pour calculer l’asymptote verticale d’une fonction, les étapes suivantes doivent être suivies :
- Trouvez le domaine de la fonction. Si tous les points sont dans le domaine, la fonction n’a pas d’asymptotes verticales.
- Calculez la limite de la fonction aux points qui ne sont pas dans le domaine.
- Les asymptotes verticales de la fonction seront toutes les valeurs dans lesquelles la limite donne l’infini.
Notez qu’une fonction peut avoir plus d’une asymptote verticale. Par exemple, le graphe de la fonction tangente a une infinité d’asymptotes verticales.
➤ Voir : caractéristiques de la fonction tangente
Exemple d’asymptote verticale
A titre d’exemple, nous allons trouver toutes les asymptotes de la fonction rationnelle suivante afin que vous puissiez voir comment cela se fait :
![]()
En général, les points où il y a des asymptotes verticales n’appartiennent pas au domaine de la fonction. Par conséquent, nous allons d’abord calculer le domaine de la fonction.
C’est une fonction rationnelle, donc on regarde quand le dénominateur s’annule pour déterminer les points qui n’appartiennent pas au domaine :
![]()
![]()
Par conséquent, le domaine de la fonction est tous les nombres réels sauf x=2 :
![]()
Donc x=2 pourrait être une asymptote verticale de la fonction. Pour le vérifier, il faut calculer la limite de la fonction en ce point :
![]()
Dans ce cas, nous avons obtenu l’indétermination d’un nombre entre zéro et, par conséquent, pour résoudre la limite, nous devons calculer les limites latérales pour savoir si elle est plus l’infini, moins l’infini ou si la limite n’existe pas. Cependant, lorsque nous calculons des asymptotes verticales, nous n’avons pas besoin de faire les limites latérales, mais l’obtention de cette indétermination suffit pour affirmer qu’il s’agit d’une asymptote verticale.
En bref, puisque la limite de la fonction quand x tend vers 2 donne l’infini, x=2 est une asymptote verticale.
Ci-dessous la fonction représentée graphiquement. Comme vous pouvez le voir, il s’approche très près de la ligne x=2 (à la fois de la gauche et de la droite) mais il ne la coupe jamais car c’est une asymptote verticale :

De plus, on peut déduire du graphe les limites latérales de la fonction au point x=2 :
![]()
Problèmes résolus d’asymptotes verticales
Exercice 1
Calculez l’asymptote verticale de la fonction rationnelle suivante :
![]()
Il n’y a pas de formule pour calculer les asymptotes verticales d’une fonction, mais il faut trouver le domaine de la fonction et voir en quels points où la fonction n’est pas définie la limite donne l’infini.
Par conséquent, nous fixons le dénominateur de la fonction rationnelle égal à 0 pour trouver les points qui n’appartiennent pas au domaine :
![]()
![]()
![]()
Ainsi, le domaine de la fonction est tous les nombres réels sauf x=1/2 :
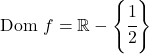
Donc x=1/2 pourrait être une asymptote verticale. Pour le vérifier, on calcule la limite de la fonction en ce point :
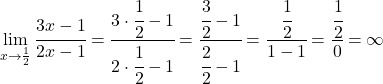
Donc x=1/2 est une asymptote verticale , puisque la limite de la fonction en ce point donne l’infini.
Exercice 2
Trouvez toutes les asymptotes verticales de la fonction fractionnaire suivante :
![]()
Tout d’abord, nous définissons le dénominateur de la fraction égal à zéro pour voir quelles valeurs ne font pas partie du domaine de la fonction :
![]()
On résout l’équation quadratique incomplète :
![]()
![]()
Le domaine de la fonction rationnelle est donc :
![]()
Ainsi, pour déterminer lesquelles de ces deux valeurs sont des asymptotes verticales, nous résolvons la limite de la fonction en chaque point :
![]()
![]()
Les deux limites donnent l’infini, donc x=3 et x=-3 sont les deux asymptotes verticales de la fonction problème .
Exercice 3
Trouvez, si vous avez, toutes les asymptotes verticales de la fonction rationnelle suivante :
![]()
➤ Voir : zéro entre zéro indétermination
Tout d’abord, nous résolvons l’équation quadratique du dénominateur pour trouver les valeurs qui annulent le dénominateur de la fraction :
![]()
![Rendered by QuickLaTeX.com \begin{aligned}\displaystyle x&=\cfrac{-b\pm\sqrt{b^2-4ac}}{2a}=\cfrac{-2\pm\sqrt{2^2-4\cdot1\cdot(-3)}}{2\cdot1}=\\[3ex]\displaystyle &=\cfrac{-2\pm\sqrt{16}}{2}=\cfrac{-2\pm 4}{2}=\begin{cases}\cfrac{-2+4}{2}=1\\[3ex]\cfrac{-2-4}{2}=-3\end{cases}\end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-9b2170358d5d1719077695aba5afa02e_l3.png)
Donc le domaine de la fonction est :
![]()
Donc, nous calculons d’abord la limite de la fonction en x=1 :
![]()
Et, d’autre part, on résout la limite de la fonction quand x tend vers -3 :
![Rendered by QuickLaTeX.com \begin{array}{l}\displaystyle\lim_{x \to -3}\frac{x+3}{x^2+2x-3}=\frac{-3+3}{(-3)^2+2\cdot(-3)-3}=\frac{0}{0}=\\[3ex]\displaystyle =\lim_{x \to -3}\frac{\cancel{x+3}}{(x-1)\cancel{(x+3)}}=\lim_{x \to -3}\frac{1}{x-1}=\frac{1}{-3-1}=-\frac{1}{4}\end{array}](https://mathority.org/wp-content/ql-cache/quicklatex.com-f0e96a48986cd110e04058e3545290a0_l3.png)
La limite précédente donne la forme indéterminée zéro entre zéro, donc pour la résoudre, nous devons factoriser les polynômes. Si vous avez des doutes sur la façon dont nous avons résolu la limite, vous pouvez voir l’explication complète de la façon de résoudre ce type d’indétermination dans le lien vers l’énoncé de l’exercice.
Dans ce cas, seule la limite de la fonction au point x=1 donne l’infini, donc x=1 est la seule asymptote verticale de la fonction .