▷ Qu'est-ce qu'un trinôme carré parfait ? (exemples)

Sur cette page, nous expliquons en quoi consiste un trinôme carré parfait et comment il est pris en compte. De plus, vous pourrez voir plusieurs exemples et vous entraîner avec des exercices étape par étape du trinôme carré parfait.

Qu’est-ce qu’un trinôme carré parfait ?

Évidemment, avant de voir la signification d’un trinôme carré parfait, vous devez savoir ce que sont les trinômes , je vous recommande donc de jeter un œil à cette page liée (où c’est expliqué en détail) avant de continuer.

Ainsi, la définition d’un trinôme carré parfait est la suivante :

En mathématiques, un trinôme carré parfait , également connu sous le nom de TCP , est le trinôme obtenu en mettant au carré un binôme.

Par conséquent, un trinôme carré parfait consiste en un polynôme avec deux carrés parfaits et un autre terme qui est le double produit des bases de ces carrés.

Comme vous pouvez le voir à partir des deux formules ci-dessus, le trinôme carré parfait est obtenu à partir de deux identités notables (ou produits notables), c’est pourquoi il est si important. Plus précisément, un trinôme carré parfait est trouvé lors de la résolution du carré d’une addition ou du carré d’une soustraction .

Exemples de trinôme carré parfait

Pour finir de comprendre le concept du trinôme carré parfait, nous allons expliquer 2 exemples étape par étape :

Exemple 1

$x^2+6x+9$

Cet exemple est un trinôme carré parfait car dans son expression algébrique il y a deux carrés parfaits (c’est-à-dire qu’ils ont une racine carrée exacte), puisque

$x^2$ et 9 sont équivalents à $x$ et 3 élevés respectivement à la puissance deux :

$(x)^2 = x^2$

$(3)^2 = 9$

Et de plus, le dernier terme restant du trinôme

$(6x)$ Il s’obtient en multipliant les bases des deux carrés précédents entre elles et par 2 :

$2\cdot x \cdot 3 = 6x$

Ainsi, toute l’identité notable complète dans cet exercice serait :

$(x+3)^2 =x^2+6x+9$

Exemple 2

$16x^2-40x+25$

Cet autre exemple est aussi un trinôme carré parfait car les 3 conditions nécessaires sont remplies : deux termes correspondent à deux carrés parfaits, et un autre terme est le résultat de la multiplication des bases de ces carrés entre elles et par 2.

$(4x)^2 = 16x^2$

$(5)^2 = 25$

$2\cdot 4x \cdot 5 =40x$

Dans ce cas le trinôme carré parfait a un monôme négatif, il correspond donc au développement de l’égalité notable d’une différence au carré :

$(4x-5)^2 = 16x^2-40x+25$

Comment factoriser un trinôme carré parfait

En algèbre, un problème très courant consiste à factoriser un trinôme carré parfait (TCP). Au cas où vous ne sauriez pas ce que cela signifie, factoriser un polynôme signifie transformer son expression en un produit de facteurs.

Ainsi, afin de factoriser ce type de trinôme algébrique, les règles suivantes doivent être respectées :

Le trinôme doit avoir deux carrés parfaits, que nous appellerons 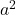$a^2$ et $b^2.$
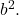
Le troisième terme restant du trinôme doit être égal au double produit des bases des deux carrés parfaits, ce qui correspond mathématiquement à l’expression $2\cdot a \cdot b.$
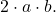
Le trinôme factorisé sera 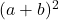$(a+b)^2$ si tous les termes du trinôme carré parfait sont positifs, sinon, si le double produit des bases des carrés a un signe négatif, le trinôme factorisé sera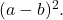 $(a-b)^2.$

Pour finir de comprendre la procédure, nous allons résoudre un exercice étape par étape :

Factoriser le trinôme carré parfait suivant :

$x^2-12x+36$

La première chose que nous devons faire est d’identifier si le trinôme a deux éléments qui sont des carrés parfaits, ou en d’autres termes, si sa racine carrée ne donne pas de nombre décimal. Dans ce problème

$x^2$ est le carré de la variable $x$ et 36 est le carré de 6 :

$\sqrt{x^2} = x$

$\sqrt{36} = 6$

Le trinôme possède donc bien deux carrés parfaits.

Dans un deuxième temps, il faut vérifier si le terme intermédiaire est équivalent au double produit des deux racines calculé à l’étape précédente :

$2 \cdot x \cdot 6 = 12x$

Cette règle est également respectée.

Ensuite, toutes les conditions sont réunies. Par conséquent, le trinôme carré parfait factorisé est le binôme formé par les deux racines trouvées (

$x$ et le nombre 6) au carré :

$x^2-12x+36=(x-6)^2$

Puisque le terme intermédiaire est négatif, il faut également mettre un signe moins entre parenthèses. Par contre, s’il était positif il faudrait ajouter une somme :

$x^2+12x+36=(x+6)^2$

Logiquement, la factorisation est une procédure compliquée donc, en plus d’essayer de faire l’exercice ci-dessous, je vous recommande de regarder ces exemples de factorisation de polynômes . Dans ce lien, nous expliquons également une méthode qui sert non seulement à factoriser les trinômes, mais aussi tout type de polynôme, et aussi rapidement.

Exercices résolus du trinôme carré parfait

Transformez les trinômes suivants en binômes carrés en appliquant la formule correspondante :

$\text{A)} \ x^2+8x+16$

$\text{B)} \ x^2-14x+49$

$\text{C)} \ x^4-20x^2+100$

$\text{D)} \ 81x^2+90x+25$

$\text{E)} \ 64x^4-176x+121$

Voir la solution

Pour convertir un trinôme carré parfait en puissance d’un binôme carré il faut utiliser les formules des identités notables du carré d’une somme et du carré d’une différence, qui sont :

$(a+b)^2 = a^2+2ab+b^2$