Sur cette page, nous expliquons ce qu’est le terme indépendant d’un polynôme et comment il est calculé. De plus, vous pourrez voir plusieurs exemples sur la façon d’identifier le terme indépendant de différents polynômes et, même, pratiquer avec des exercices résolus.
Quel est le terme indépendant d’un polynôme ?
La définition du terme indépendant d’un polynôme est la suivante :
En mathématiques, le terme indépendant d’un polynôme est le terme qui n’a pas de variable. Par conséquent, le terme indépendant d’un polynôme correspond au monôme de degré zéro du polynôme.
Par exemple, le terme indépendant du polynôme suivant est 7 :
Dans le polynôme de l’exemple précédent, le terme qui n’a pas de partie littérale, c’est-à-dire qu’il n’a pas de x, est le nombre 7. Pour cette raison, le terme indépendant dudit polynôme est 7.
Bien que le terme indépendant d’un polynôme semble être un concept très simple, sachez qu’il est très utile pour certains calculs de polynômes. Par exemple, la procédure pour trouver les racines d’un polynôme commence à son terme indépendant. Si vous voulez en savoir plus sur la façon de trouver les racines (ou les zéros) d’un polynôme, vous pouvez consulter ce lien, où vous pouvez également voir des exemples et vous pouvez vous entraîner avec des exercices résolus étape par étape.
Exemples de termes indépendants de polynômes
Une fois que nous connaissons la signification du terme indépendant d’un polynôme, nous allons voir plusieurs exemples de comment trouver le terme indépendant d’un polynôme :
- Exemple de terme indépendant d’un polynôme de degré 4 :
Le polynôme dans cet exemple est un polynôme monique et le terme qui n’a pas de variable est 5, donc la valeur du terme indépendant du polynôme est 5.
- Exemple de terme indépendant d’un polynôme de degré 5 :
L’élément de ce polynôme qui n’est pas accompagné de la variable x est -2, c’est donc le terme indépendant du polynôme. Notez que le signe négatif du nombre est également inclus dans le terme indépendant.
- Exemple de terme indépendant d’un polynôme de degré 8 :
Tous les monômes de ce polynôme ont une variable sauf +1, donc le terme indépendant du polynôme est +1.
Enfin, une des propriétés du terme indépendant est que la valeur numérique d’un polynôme pour x=0 est toujours égale à son terme indépendant. Si vous êtes plus intéressé par cette chose curieuse, vous pouvez consulter sur la page liée comment la valeur numérique d’un polynôme est calculée, en plus, vous trouverez également plusieurs exemples de la façon dont cela est fait et vous pourrez pratiquer avec des exercices résolu pas à pas.
Exercice résolu sur le terme indépendant d’un polynôme
Pour finir d’assimiler ce qu’est le terme indépendant d’un polynôme, nous vous proposons de faire l’exercice que nous résolvons ci-dessous :
- Étant donné le polynôme
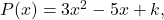calcule la valeur du terme indépendant
pour qu’il soit rempli
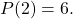
La première chose à faire pour résoudre ce problème est d’essayer de déterminer
pourtant:
Nous calculons la puissance:
On fait les multiplications :
Et nous soustrayons comme termes :
Ainsi, pour que la condition de l’énoncé soit remplie, il faut égaliser l’expression algébrique obtenue à 6 :
Il suffit donc de résoudre l’équation résultante :
En conclusion, le terme indépendant du polynôme doit être 4.
Enfin, il faut savoir que le terme indépendant d’un polynôme est aussi important pour appliquer correctement la règle de Ruffini. Au cas où vous ne sauriez pas ce que c’est, la règle de Ruffini est une méthode utilisée pour diviser rapidement des polynômes. Ici vous pouvez voir comment faire la règle de Ruffini et comment elle se rapporte au terme indépendant d’un polynôme.