▷ Taux de variation moyen et instantané (exercices résolus)

Nous expliquons ici ce que sont le taux de changement, le taux de changement moyen et le taux de changement instantané. Vous pourrez voir plusieurs exemples sur la façon de calculer le taux de changement et, en plus, vous pourrez vous entraîner avec des exercices résolus étape par étape sur le taux de changement.

Quel est le taux de variation ?

En mathématiques, le taux de variation (TV) d’une fonction est la différence des valeurs d’une fonction en deux points différents. Par conséquent, pour calculer le taux de variation entre deux points, les valeurs de la fonction en ces deux points doivent être soustraites.

$\text{TV}[a,b]=f(b)-f(a)$

Par exemple, si deux images d’une fonction sont f(2)=1 et f(5)=7, leur taux de changement est :

$\text{TV}[2,5]=f(5)-f(2)=7-1=6$

Nous venons de voir la signification mathématique du taux de changement, mais en économie le concept de taux de changement signifie ce qui suit :

En économie, le taux de variation entre deux valeurs est la différence entre elles exprimée en pourcentage, c’est-à-dire que le taux de variation d’une variable entre différentes périodes est sa variation relative. Par conséquent, pour calculer le taux de variation, les valeurs des deux périodes différentes sont soustraites et le résultat obtenu est divisé par la valeur de la période initiale.

$\text{TV}[t,t+n]=\cfrac{Y_{t+n}-Y_t}{Y_t}\cdot 100$

Par exemple, si la valeur de certaines actions est passée de 35 € à 50 € en un mois, son rythme d’évolution sera :

$\text{TV}[t,t+1]=\cfrac{50-35}{35}\cdot 100=42,86 \ \%$

Compte tenu des deux significations possibles du taux de variation, dans cet article, nous nous concentrerons sur la compréhension de la définition mathématique du taux de variation. Deux types de taux de variation peuvent être distingués : le taux de variation moyen et le taux de variation instantané. Ci-dessous vous avez l’explication de chaque type.

Taux de variation moyen

Le taux de variation moyen (TVM) d’une fonction dans un intervalle est le nombre d’unités que la fonction augmente (ou diminue) pour chaque unité que sa variable indépendante augmente. Par conséquent, le taux de variation moyen d’une fonction est calculé en divisant la croissance de la fonction dans un intervalle par l’amplitude de ce même intervalle.

$\text{TVM}[a,b]=\cfrac{f(b)-f(a)}{b-a}$

Afin que vous puissiez voir comment le taux de variation moyen est calculé, nous avons résolu ci-dessous un exemple étape par étape.

Exemple de calcul du taux de variation moyen d’une fonction

Calculez le taux de variation moyen dans l’intervalle [2,5] de la fonction suivante :

$f(x) = x^2-1$

Tout d’abord, on calcule la valeur de la fonction à x=2 et x=5 :

$f(5)= 5^2-1=25-1=24$

$f(2)=2^2-1=4-1=3$

Et puis on calcule le taux moyen de variation de la fonction dans l’intervalle simplement en appliquant la formule :

$\text{TVM} [a,b] = \cfrac{f(b)-f(a)}{b-a}$

$\text{TVM} [2,5]=\cfrac{f(5)-f(2)}{5-2} = \cfrac{24 - 3}{5-2} = \cfrac{21}{3} = \bm{7}$

Puisque le résultat de TVM[2,5] est positif, cela signifie que la fonction croît dans l’intervalle [2,5]. En revanche, si le résultat avait été négatif, cela signifierait que la fonction diminue dans cet intervalle.

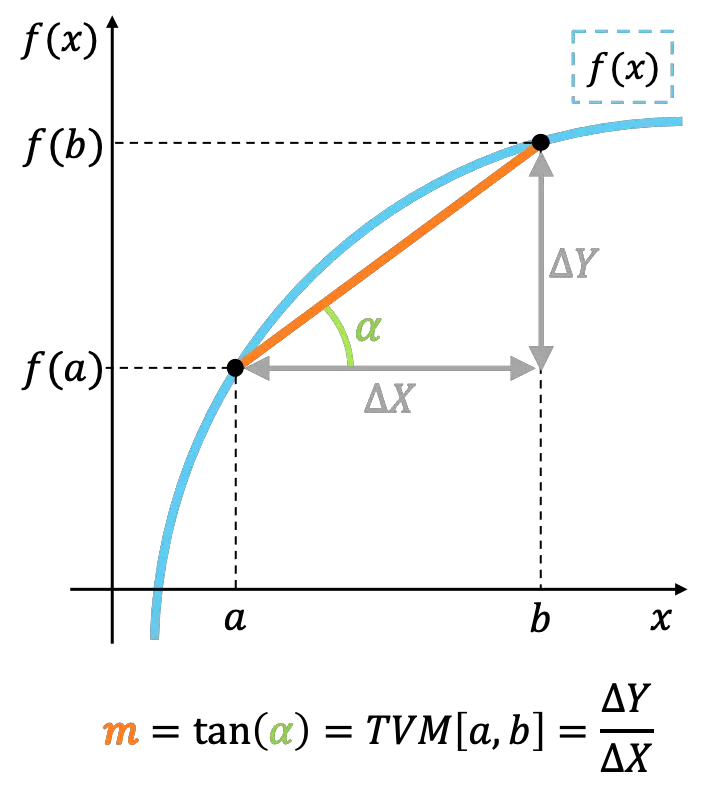
Interprétation géométrique du taux de changement moyen

Géométriquement, le taux de variation moyen d’une fonction dans un intervalle représente la pente de la ligne joignant les points extrêmes de l’intervalle.

Taux de variation instantané

Le taux de variation instantané (TVI) d’une fonction en un point est la limite infinitésimale de l’augmentation relative de la fonction sur un intervalle. Par conséquent, le taux de changement instantané est calculé en résolvant la limite du quotient de f(a+h)-f(a) par h lorsque h tend vers zéro.

$\displaystyle\text{TVI}(a)=\lim_{h \to 0}\frac{f(a+h)-f(a)}{h}$

La valeur du taux de changement instantané peut être positive, négative ou nulle, et signifie que la fonction à ce point augmente, diminue ou reste la même respectivement à ce point.

Exemple de calcul du taux de variation instantané d’une fonction

Calculez le taux de changement instantané au point x=2 de la fonction suivante :

$f(x) = x^2$

Pour calculer le taux de variation instantané, nous devons appliquer la formule :

$\text{TVI} (a) = \lim\limits_{h \to 0} \cfrac{f(a+h)-f(a)}{h}$

$\text{TVI} (2) = \lim\limits_{h \to 0} \cfrac{f(2+h)-f(2)}{h} = \lim\limits_{h \to 0} \cfrac{(2+h)^2-2^2}{h}$

On résout l’identité notable :

$\lim\limits_{h \to 0} \cfrac{2^2+h^2+2\cdot 2 \cdot h -2^2}{h} = \lim\limits_{h \to 0} \cfrac{4+h^2+4h -4}{h} = \lim\limits_{h \to 0} \cfrac{h^2+4h}{h}$

➤ Si vous ne vous souvenez plus des formules des identités notables , vous trouverez toutes les formules sur notre site spécialisé dans les polynômes : www.polinomios.org

Essayons maintenant de résoudre la limite :

$\lim\limits_{h \to 0} \cfrac{h^2+4h}{h} = \cfrac{0^2+4\cdot 0}{0} =\cfrac{0}{0}$

Mais on retrouve l’indétermination zéro entre zéro, donc :

$\lim\limits_{h \to 0} \cfrac{h^2+4h}{h}= \lim\limits_{h \to 0} \cfrac{\cancel{h}(h+4)}{\cancel{h}} = \lim\limits_{h \to 0} (h+4)$

➤ Voir : comment résoudre une limite avec une indétermination nulle entre zéro

Et enfin nous résolvons la limite :

$\lim\limits_{h \to 0} (h+4) = 0 +4 = \bm{4}$

Pourtant:

$\mathbf{TVI} \bm{(2) = 4}$

Puisque le résultat de TVI(2) est positif, cela signifie que la fonction croît à x=2. En revanche, si le résultat avait été négatif, cela signifierait que la fonction diminue à ce stade.

Interprétation géométrique du taux de changement instantané

Géométriquement, le taux de changement instantané d’une fonction en un point représente la pente de la ligne tangente à la fonction en ce même point.

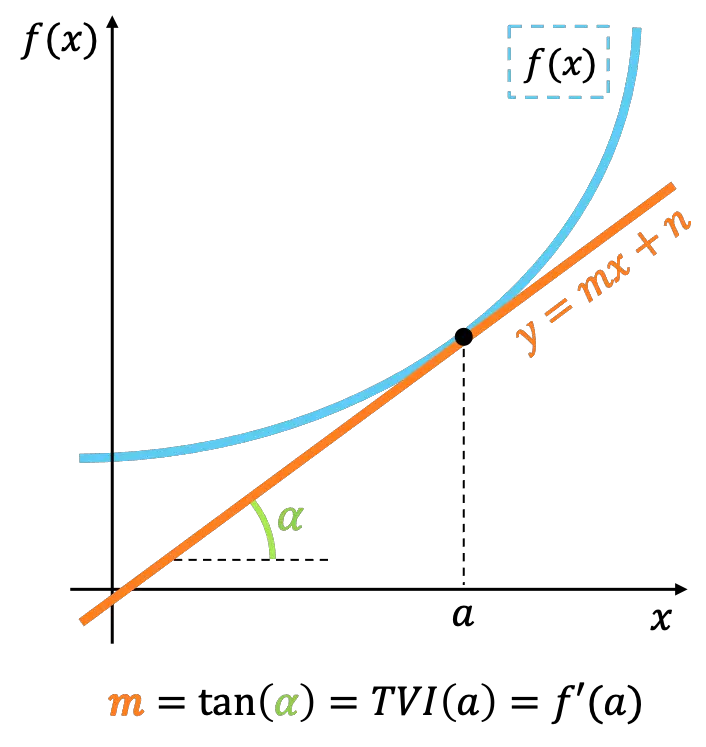
Si vous regardez attentivement, la signification du taux de variation instantané est équivalente au concept de dérivée d’une fonction . Ainsi, le taux de variation instantané sert également à calculer la valeur de la dérivée d’une fonction en un point.

Exercices résolus sur le taux de changement

Exercice 1

Calculez la valeur du taux de variation de la fonction suivante dans l’intervalle [1,3].

$f(x)=x^2-5$

Voir la solution

Tout d’abord, on détermine la valeur de la fonction aux extrémités de l’intervalle :

$f(1)=1^2-5=1-5=-4$

$f(3)=3^2-5=9-5=4$

Et maintenant, nous appliquons la formule du taux de changement :

$\text{TV}[a,b]=f(b)-f(a)$

$\text{TV}[1,3]=f(3)-f(1)=4-(-4)=4+4=\bm{8}$

Exercice 2

Calculez le taux de changement moyen (TVM) de la fonction suivante sur l’intervalle [1,4] :

$f(x)=2x+1$

Voir la solution

Nous calculons d’abord les images de la fonction à x=1 et x=4.

$f(4)=2\cdot4+1=9$

$f(1)=2\cdot 1+1=3$

Et nous appliquons la formule du taux de variation moyen :

$\text{TVM} [a,b] = \cfrac{f(b)-f(a)}{b-a}$

$\text{TVM} [1,4] = \cfrac{f(4)-f(1)}{4-1} = \cfrac{9-3}{4-1}=\cfrac{6}{3} = \bm{2}$

Exercice 3

Trouvez le taux de variation moyen de la fonction suivante dans l’intervalle [-1,3] :

$f(x)=(x+1)^2$

Voir la solution

Pour déterminer le taux de variation moyen, nous devons d’abord calculer f(-1) et f(3) :

$f(3)=(3+1)^2=(4)^2=16$

$f(-1)=((-1)+1)^2=(0)^2=0$

Nous utilisons maintenant la formule pour le taux de variation moyen :

$\text{TVM} [a,b] = \cfrac{f(b)-f(a)}{b-a}$

$\text{TVM} [-1,3] = \cfrac{f(3)-f(-1)}{3-(-1)} = \cfrac{16-0}{3+1}=\cfrac{16}{4} = \bm{4}$

Exercice 4

Calculez le taux de variation moyen dans l’intervalle [2,4] de la fonction représentée dans le graphique suivant :

Voir la solution

Nous appliquons la formule du taux de variation moyen :

$\text{TVM} [a,b] = \cfrac{f(b)-f(a)}{b-a}$

$\text{TVM} [2,4]=\cfrac{f(4)-f(2)}{4-2}$

Comme nous le voyons dans la formule, nous devons trouver la valeur de f(4) et f(2). Et cela peut être facilement fait en regardant la représentation graphique de la fonction :

$f(4)=5$

$f(2)=1$

Et maintenant que nous connaissons les valeurs de la fonction, nous les substituons dans la formule :

$\text{TVM}[2,4]=\cfrac{f(4)-f(2)}{4-2}=\cfrac{5-1}{4-2}=\cfrac{4}{2}=\bm{2}$

Exercice 5

Calculez le taux de variation instantané de la fonction suivante au point x=2 :

$f(x)=3x$

Voir la solution

Pour déterminer le taux de variation instantané de la fonction au point x=2 nous appliquons sa formule correspondante :

$\text{TVI}(a)=\lim\limits_{h \to 0} \cfrac{f(a+h)-f(a)}{h}$

$\begin{array}{l}\text{TVI}(2)=\lim\limits_{h \to 0} \cfrac{f(2+h)-f(2)}{h}=\\[4ex]=\lim\limits_{h \to 0} \cfrac{3(2+h)-3\cdot 2}{h} =\\[4ex]=\lim\limits_{h \to 0} \cfrac{6+3h-6}{h}= \lim\limits_{h \to 0} \cfrac{3h}{h} =\\[4ex]=\lim\limits_{h \to 0} \cfrac{3\cancel{h}}{\cancel{h}}=\lim\limits_{h \to 0} 3 = \bm{3}\end{array}$

Exercice 6

Déterminez le taux de variation instantané (TVI) de la fonction suivante au point x=1 :

$f(x)=x^2+1$

Voir la solution

Nous appliquons la formule du taux de variation instantané :

$\text{TVI} (a) = \lim\limits_{h \to 0} \cfrac{f(a+h)-f(a)}{h}$

$\text{TVI} (1) = \lim\limits_{h \to 0} \cfrac{f(1+h)-f(1)}{h}$

Ensuite, on calcule

$f(1+h)$ et $f(1):$

$f(1+h) = (1+h)^2+1$

$f(1)=1^2+1=1+1=2$

Et on substitue les valeurs trouvées dans la limite :

$\text{TVI} (1) = \lim\limits_{h \to 0} \cfrac{f(1+h)-f(1)}{h}= \lim\limits_{h \to 0} \cfrac{(1+h)^2+1-2}{h} =\lim\limits_{h \to 0} \cfrac{(1+h)^2-1}{h}$

On résout le produit notable :

$\lim\limits_{h \to 0} \cfrac{1^2+h^2+2\cdot 1 \cdot h-1}{h}=\lim\limits_{h \to 0} \cfrac{1+h^2+2h-1}{h}=\lim\limits_{h \to 0} \cfrac{h^2+2h}{h}$

Essayons maintenant de résoudre la limite :

$\lim\limits_{h \to 0} \cfrac{h^2+2h}{h}=\cfrac{0^2+2\cdot 0}{0} = \cfrac{0}{0}$

Mais on retrouve la forme indéterminée zéro divisé par zéro, on factorise donc le polynôme du numérateur de la fraction et on simplifie :

$\lim\limits_{h \to 0} \cfrac{h^2+2h}{h}=\lim\limits_{h \to 0} \cfrac{h(h+2)}{h} = \lim\limits_{h \to 0} \cfrac{\cancel{h}(h+2)}{\cancel{h}}= \lim\limits_{h \to 0}(h+2)$

➤ Si vous ne savez pas comment résoudre l’indétermination nulle entre zéro , vous pouvez voir l’explication complète dans le lien ci-dessus sur la façon de résoudre une limite avec indétermination nulle entre zéro.

Et enfin, nous résolvons la limite :

$\lim\limits_{h \to 0}(h+2) = 0+2 =\bm{2}$

En résumé, le taux de changement instantané de la fonction au point x=1 est égal à 2.

$\mathbf{TVI} \bm{(1) = 2}$

Exercice 7

Trouvez le taux de variation instantané de la fonction suivante au point x=2 :

$f(x)=4x^2-x+3$

Voir la solution

Nous utilisons d’abord la formule du taux de changement instantané :

$\text{TVI} (a) = \lim\limits_{h \to 0} \cfrac{f(a+h)-f(a)}{h}$

$\text{TVI} (2) = \lim\limits_{h \to 0} \cfrac{f(2+h)-f(2)}{h}$

Nous calculons

$f(2+h)$ et $f(2):$

$f(2+h) = 4(2+h)^2-(2+h)+3=4(2+h)^2-h+1$

$f(2) =4\cdot 2^2-2+3=4\cdot 4-2+3 =17$

Et on substitue les valeurs trouvées dans la limite :

$\text{TVI} (2) = \lim\limits_{h \to 0} \cfrac{f(2+h)-f(2)}{h}=\\[4ex]=\lim\limits_{h \to 0} \cfrac{4(2+h)^2-h+1-17}{h}=\\[4ex]= \lim\limits_{h \to 0} \cfrac{4(2+h)^2-h-16}{h}$

On calcule l’égalité notable :

$\lim\limits_{h \to 0} \cfrac{4(2^2+h^2+2\cdot 2 \cdot h)-h-16}{h}=\lim\limits_{h \to 0} \cfrac{4(4+h^2+4h)-h-16}{h}$

On opère sur le numérateur :

$\lim\limits_{h \to 0} \cfrac{16+4h^2+16h-h-16}{h}=\lim\limits_{h \to 0} \cfrac{4h^2+15h}{h}$

Essayons maintenant de résoudre la limite :

$\lim\limits_{h \to 0} \cfrac{4h^2+15h}{h}=\cfrac{4\cdot0^2+15\cdot 0}{0} = \cfrac{0}{0}$

Mais on obtient l’indétermination zéro divisé par zéro, donc on factorise les polynômes et on simplifie :

$\lim\limits_{h \to 0} \cfrac{4h^2+15h}{h}=\lim\limits_{h \to 0} \cfrac{h(4h+15)}{h}=\lim\limits_{h \to 0} \cfrac{\cancel{h}(4h+15)}{\cancel{h}}= \lim\limits_{h \to 0}(4h+15)$

Et enfin, nous résolvons la limite :

$\lim\limits_{h \to 0}(4h+15)=4\cdot 0+15 =\bm{15}$

Pourtant:

$\mathbf{TVI} \bm{(2) = 15}$

Taux de changement moyen et instantané

Quel est le taux de variation ?

Taux de variation moyen

Exemple de calcul du taux de variation moyen d’une fonction

Interprétation géométrique du taux de changement moyen

Taux de variation instantané

Exemple de calcul du taux de variation instantané d’une fonction

Interprétation géométrique du taux de changement instantané

Exercices résolus sur le taux de changement

Exercice 1

Exercice 2

Exercice 3

Exercice 4

Exercice 5

Exercice 6

Exercice 7

Leave a Comment Cancel Reply