Sur cette page vous découvrirez quelles sont les racines d’un polynôme et comment elles sont calculées. De plus, vous pourrez voir des exemples et des exercices résolus étape par étape sur les racines d’un polynôme.
Quelles sont les racines d’un polynôme ?
En mathématiques, les racines (ou zéros) d’un polynôme sont les valeurs qui annulent le polynôme. Autrement dit, les racines d’un polynôme sont toutes ces valeurs qui, lorsqu’elles sont évaluées dans le polynôme, ont une valeur numérique égale à 0.
Finalement,
![]() est une racine du polynôme
est une racine du polynôme![]() Ouais
Ouais ![]()
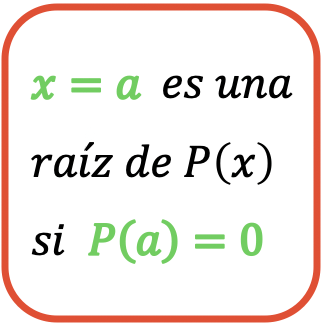
Par exemple, si nous avons le polynôme suivant :
![]()
On peut vérifier que l’une des racines du polynôme est 1, puisque la valeur numérique du polynôme en x=1 est égale à zéro :
![]()
En revanche, 3 n’est pas une racine du polynôme car ce n’est pas une valeur qui annule le polynôme, ou en d’autres termes, la valeur numérique du polynôme en x=3 est différente de zéro :
![]()
Vous comprenez sûrement mieux maintenant ce qu’est la racine d’un polynôme, mais n’aimeriez-vous pas savoir combien de racines possède un polynôme ? Ou comment trouver toutes les racines d’un polynôme ? Eh bien, c’est précisément ce que nous allons voir dans la section suivante.
Comment calculer toutes les racines d’un polynôme ?
Pour trouver toutes les racines d’un polynôme, il faut suivre les étapes suivantes :
- Tout d’abord, tous les diviseurs du terme indépendant du polynôme sont calculés.
- Deuxièmement, toutes les valeurs trouvées à l’étape précédente sont évaluées dans le polynôme.
- Enfin, si lors de l’évaluation d’un nombre dans le polynôme sa valeur numérique est égale à zéro, ledit nombre est une racine du polynôme. Dans le cas contraire, ledit nombre ne correspond pas à une racine du polynôme.
Cette procédure est déduite du théorème des restes , cliquez sur ce lien pour découvrir la raison de cette procédure particulière.
Exemple de calcul des racines d’un polynôme
Ci-dessous, nous allons résoudre un exemple étape par étape afin que vous puissiez mieux comprendre comment prendre les racines d’un polynôme.
- Quelles sont toutes les racines du polynôme suivant ?
![]()
Tout d’abord, il faut trouver les diviseurs du terme indépendant, car toute racine d’un polynôme est aussi diviseur du terme indépendant. Ainsi, les diviseurs de 6 sont :
Diviseurs de 6 : +1, -1, +2, -2, +3, -3
N’oubliez pas que si un nombre est un diviseur, son négatif est également un diviseur. Puisqu’un nombre est divisible par des nombres positifs et négatifs.
Ainsi, les racines ou zéros possibles du polynôme sont : ±1, ±2, ±3. Par conséquent, nous devons déterminer la valeur numérique du polynôme pour toutes ces valeurs. Et, pour ce faire, on substitue ces valeurs dans l’expression du polynôme où il y a un x :
![]()
![]()
![]()
![]()
![]()
![]()
Ainsi le polynôme disparaît uniquement lorsque la variable x est +2 ou +3, voici donc les racines du polynôme :
Racines ou zéros du polynôme : +2 et +3
Par contre, remarquez que le polynôme a autant de racines que son degré, c’est-à-dire que puisque le polynôme est du deuxième degré, il a deux racines. Dans les propriétés des racines d’un polynôme (ci-dessous), nous verrons pourquoi cette caractéristique est toujours valable pour tout polynôme.
Nous venons de voir une manière de trouver les racines d’un polynôme. Cependant, il existe encore d’autres méthodes pour y parvenir, par exemple vous pouvez également trouver les racines d’un polynôme avec la règle de Ruffini. Cliquez sur le lien suivant pour voir des exemples de la règle de Ruffini , vous découvrirez ici en quoi consiste cette méthode bien connue et, également, quelles sont les différences entre les deux procédures.
Propriétés des racines d’un polynôme
Les racines ou zéros d’un polynôme ont les caractéristiques suivantes :
- Comme nous l’avons vu précédemment, les racines entières (ou zéros) d’un polynôme sont des diviseurs du terme indépendant du polynôme.
- Si l’on connaît toutes les racines d’un polynôme, on peut exprimer ledit polynôme sous forme de produits de binômes du type
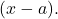
Par exemple, le polynôme
![]() Il a 3 racines qui sont
Il a 3 racines qui sont![]() et
et![]() On peut donc réécrire le polynôme sous la forme de 3 multiplications de facteurs, chacune formée par la variable
On peut donc réécrire le polynôme sous la forme de 3 multiplications de facteurs, chacune formée par la variable![]() et une racine a changé de signe :
et une racine a changé de signe :
![Rendered by QuickLaTeX.com \displaystyle\definecolor{vermell}{HTML}{F44336}\definecolor{blau}{HTML}{2196F3}\definecolor{verd}{HTML}{27AE60} P(x) =x^3+3x^2-x-3 \ \longrightarrow \ \text{ra\'ices} \begin{cases} x=\color{verd}\bm{+1} \\[2ex] x=\color{vermell}\bm{-1} \\[2ex] x=\color{blau}\bm{-3}\end{cases}](https://mathority.org/wp-content/ql-cache/quicklatex.com-ce071610927d2723c8ac2e7b299c1c5d_l3.png)
![]()
C’est ce qu’on appelle la factorisation de polynômes. En fait, l’une des principales applications de la détermination des racines d’un polynôme est qu’elles servent à le factoriser. Dans le lien suivant, vous pourrez découvrir en quoi consiste cette opération très spéciale et, en plus, vous pourrez vous entraîner avec des exercices de factorisation polynomiale résolus .
- Un polynôme a autant de racines que son degré l’indique. Ainsi, un polynôme du deuxième degré aura 2 racines, un polynôme du troisième degré aura 3 racines, un polynôme du quatrième degré aura 4 racines, et ainsi de suite.
- Si un polynôme n’a pas de terme indépendant, cela signifie qu’une de ses racines est 0. Ensuite, le reste des racines doivent être des diviseurs du coefficient du monôme du degré le plus bas.
Par exemple, le polynôme suivant n’a pas de terme indépendant :
![]()
Donc une racine du polynôme doit nécessairement être 0. Et le reste des racines sont des diviseurs du coefficient du terme de degré le plus bas, soit -2. Plus précisément, les autres racines sont
![]() et
et![]() donc toutes les racines du polynôme sont :
donc toutes les racines du polynôme sont :
Racines ou zéros du polynôme : 0, +1 et -2
- Lorsque les racines d’un polynôme ne peuvent être déterminées, on dit que c’est un polynôme irréductible.
Par exemple, nous allons essayer de calculer les racines du polynôme suivant :
![]()
Les seules racines possibles du polynôme sont les diviseurs de -1, c’est-à-dire -1 et +1. Nous évaluons donc le polynôme à ces valeurs :
![]()
![]()
En aucun cas le polynôme n’est annulé, il n’a donc pas de racines et, par conséquent, c’est un polynôme irréductible.
- Lorsque le polynôme est composé du produit de plusieurs polynômes, il n’est pas nécessaire de faire ce produit pour calculer les racines, mais les racines du polynôme sont les racines de chaque facteur multiplié.
A titre d’exemple, si l’on a le polynôme suivant :
![]()
De la deuxième propriété des racines des polynômes, on peut déduire que la racine du polynôme de gauche est +2 et la racine du polynôme de droite est -1.
![]()
![]()
Ainsi, les racines du polynôme résultant de la multiplication des deux facteurs sont leurs racines respectives, soit +2 et -1.
![Rendered by QuickLaTeX.com \displaystyle P(x) = (x-2) \cdot (x+1) \ \longrightarrow \ \text{ra\'ices} \ \begin{cases}x=+2 \\[2ex] x=-1 \end{cases}](https://mathority.org/wp-content/ql-cache/quicklatex.com-416399918b5a2a051a6bfc7343ef7960_l3.png)
Exercices résolus sur les racines des polynômes
Exercice 1
Déterminer si
![]() est une racine du polynôme suivant :
est une racine du polynôme suivant :
![]()
Pour savoir si
![]() est une racine du polynôme, nous devons l’évaluer à cette valeur. Pourtant:
est une racine du polynôme, nous devons l’évaluer à cette valeur. Pourtant:
![Rendered by QuickLaTeX.com \begin{aligned}P(-4)& =(-4)^3+2\cdot (-4)^2-11\cdot (-4) -12 \\[2ex] & = -64+2\cdot 16 +44 -12 \\[2ex] & = -64+32+44 -12 \\[2ex] & = 0 \end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-0c88c4456693b0c57d55aba68287414c_l3.png)
La valeur numérique du polynôme dans
![]() est nul, c’est donc effectivement une racine du polynôme.
est nul, c’est donc effectivement une racine du polynôme.
Exercice 2
Calculez toutes les racines du polynôme suivant :
![]()
Tout d’abord, pour trouver les racines possibles du polynôme, il faut trouver les diviseurs du terme indépendant. Ainsi, les diviseurs de 2 sont :
Diviseurs de 2 : +1, -1, +2, -2
Les racines ou zéros possibles du polynôme sont donc ±1 et ±2. Par conséquent, nous devons calculer combien vaut le polynôme dans toutes ces valeurs :
![]()
![]()
![]()
![]()
Ainsi, le polynôme disparaît lorsque x vaut +1 ou +2, voici donc les racines du polynôme :
Racines ou zéros du polynôme : +1 et +2
Exercice 3
Trouvez les racines du polynôme suivant :
![]()
Il faut d’abord trouver les diviseurs du terme indépendant, puisque la racine d’un polynôme est aussi un diviseur du terme indépendant. Ainsi, les diviseurs de 4 sont :
Diviseurs de 4 : +1, -1, +2, -2, +4, -4
Les racines ou zéros possibles du polynôme sont donc ±1, ±2 et ±4. Il faut donc trouver la valeur numérique du polynôme dans toutes ces valeurs :
![]()
![]()
![]()
![]()
![]()
![]()
Ainsi, le polynôme disparaît uniquement lorsque x vaut +1, +2 ou -2, voici donc les racines du polynôme :
Racines ou zéros du polynôme : +1, +2 et -2
Exercice 4
Trouvez les racines du polynôme suivant :
![]()
Dans ce cas, le polynôme n’a pas de terme indépendant. Par conséquent, selon la quatrième propriété des racines expliquée ci-dessus, nous savons que l’une des racines du polynôme doit être 0.
Racines du polynôme :
![]()
De plus, dans ce cas, les racines possibles ne sont pas les diviseurs du terme indépendant, mais plutôt celles du coefficient du terme de degré le plus bas, soit 8 :
Diviseurs de 8 : +1, -1, +2, -2, +4, -4, +8, -8
Ainsi, les racines ou zéros possibles du polynôme sont ±1, ±2, ±4 et ±8. Il faut donc calculer la valeur numérique du polynôme à toutes ces valeurs :
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Ainsi le polynôme disparaît lorsque x vaut +2 ou +4, donc ces valeurs sont les racines du polynôme. Cependant, il faut également ajouter la racine 0 que nous avons trouvée au début du problème. En conclusion, toutes les racines du polynôme sont :
Racines ou zéros du polynôme : 0, +2 et +4
Exercice 5
Utilisez les propriétés des racines des polynômes pour calculer les racines du polynôme suivant :
![]()
Comme nous l’avons vu dans la sixième propriété des racines, lorsque le polynôme est formé par le produit de facteurs, il n’est pas nécessaire de calculer toutes les racines, puisque les racines du polynôme entier sont les racines de chaque facteur.
De plus, de la deuxième propriété des racines des polynômes, on peut déduire que la racine du premier facteur est +1 et la racine du deuxième facteur est -3.
![]()
![]()
Il suffit donc de trouver les racines du dernier facteur. Pour ce faire, on retrouve les diviseurs du terme indépendant (-2) :
Diviseurs de -2 : +1, -1, +2, -2
Ainsi, les racines ou zéros possibles du dernier polynôme sont ±1 et ±2. Avec lequel nous devons calculer la valeur numérique dudit polynôme dans toutes ces valeurs :
![]()
![]()
![]()
![]()
![]()
Les racines du polynôme de droite sont donc -1 et 2.
Par conséquent, les racines du polynôme entier sont toutes les racines trouvées :
Racines ou zéros du polynôme : +1, -1, +2, -3