Polynôme

Un monôme est une expression algébrique formée par un coefficient (valeur numérique) qui multiplie une variable par un exposant, par exemple l’expression 4x² est un monôme. Donc à partir de ce concept mathématique, on arrive au polynôme qui est un ensemble d’additions et de soustractions de plusieurs monômes. Dans l’image ci-dessus, vous pouvez voir un exemple de la structure d’un polynôme composé de plusieurs monômes.

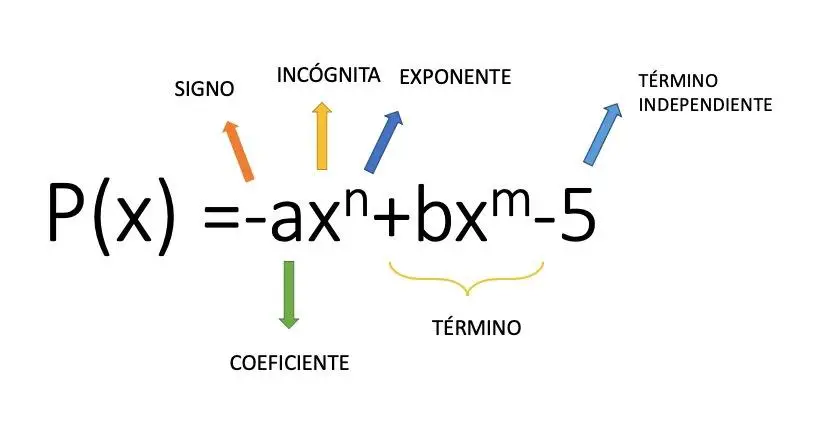
types de polynômes

Grâce à l’exposant d’un certain monôme, nous pouvons classer les polynômes en différents types. Nous pouvons classer ces expressions en catégories telles que : polynôme du premier degré, polynôme du second degré, polynôme du troisième degré, etc. Fondamentalement, vous devez identifier le monôme qui a le plus grand exposant et qui sera le degré du polynôme . Et une fois que vous le connaissez, vous pouvez le classer dans l’un des types dont nous venons de parler.

Polynôme de plusieurs variables

De plus, il existe également une autre façon d’organiser les polynômes, qui est en fonction du nombre de monômes qui les forment. Par exemple, si nous avons un binôme , cela équivaudra à avoir un polynôme à deux termes, si nous avons un trinôme , cela équivaudra à avoir un polynôme à trois termes, etc. Toutes ces manières de cataloguer les polynômes ont une infinité de sous-catégories. Puisque ces expressions peuvent être composées de tous les monômes que nous voulons et peuvent également avoir n’importe quel degré.

Caractéristiques et propriétés des polynômes

• Degré absolu d’un polynôme : dans la section précédente, nous avons discuté de la définition du degré relatif. Mais dans le cas de polynômes formés par plus d’une variable, nous avons le degré absolu qui équivaut à la somme maximale des exposants de toutes les variables de ce monôme. Par exemple, dans le monôme 5x²y³, le degré absolu est égal à 2 + 3 = 5.
• Polynôme ordonné : Nous définissons un polynôme ordonné par rapport à une variable lorsque les exposants de cette variable sont disposés en ordre croissant ou décroissant. Par exemple, si on trouve ce polynôme P(x) = 3x + 4x³ – x², dans ce cas il ne sera pas ordonné. Donc, on devrait le corriger et on obtiendrait ce résultat : P(x) = 4x³ – x² + 3x.
• Polynôme complet : Lorsque nous trouvons un polynôme qui a des monômes avec tous les exposants possibles (du degré le plus élevé au terme indépendant), nous disons qu’il s’agit d’un polynôme complet . Par exemple, l’expression suivante : P(x) = 3 x² + 2x – 4 est de ce type car il n’y a pas d’exposant manquant entre 2 et 0.
• Polynôme homogène: est ce polynôme qui a un degré absolu égal dans chacun de ses monômes. Les variables peuvent avoir des valeurs différentes dans l’exposant, mais la somme des exposants des variables dans tous les monômes doit nécessairement être la même. Par exemple : P(x) = x²y³z + 3 x ⁴ yz, les deux sommes donnent six 2 + 3 + 1 = 4 + 1 + 1 = 6.
• Polynômes identiques : lorsque nous trouvons deux ou plusieurs polynômes qui partagent les coefficients des mêmes termes, alors nous dirons qu’il s’agit de polynômes identiques. Ci-dessous vous pouvez voir un exemple entre deux polynômes : P(x) = 2x + 27 et Q(x) = 5 (x + 3) – 3 (x – 4), ils seront identiques car ils partagent les coefficients de chaque exposant : 2x = 5x – 3x et 27 = 15 + 12.
• Polynôme nul : ce polynôme n’a que des coefficients nuls (égaux à zéro), donc la valeur totale du polynôme sera également nulle. Le polynôme P(x) = 0x³ + 0x² – 0x – 0 est un exemple clair de ce type de polynôme, mais il ne faut pas le confondre avec Q(x) = 0, car dans ce cas vous formez une équation et cela ne signifie pas que tous les coefficients de Q(x) sont 0.

Valeur numérique d’un polynôme

La valeur numérique d’un polynôme est le résultat que nous obtiendrons en substituant la variable de cette expression à un nombre. Nous devons simplement résoudre ce polynôme comme s’il s’agissait d’une opération combinée . Ensuite, nous expliquerons les trois méthodes que vous pouvez utiliser pour obtenir la valeur numérique d’une expression de ce style.

• Remplacement direct : lorsqu’on nous donne directement les valeurs correspondant à chacune des variables du polynôme, il suffit de substituer ces variables à ces nombres. De cette manière, si nous avons le polynôme P(x) = 2x² – x + 4 et qu’on nous dit que x = 3, alors la valeur numérique du polynôme sera égale à 2 · 3² – 3 + 4 = 19.
• Résolution de la variable : nous appliquerons ce cas lorsqu’ils ne nous donnent pas directement la valeur de la variable, mais qu’ils nous donnent une équivalence. Par exemple, P(2) si P(x – 1) = x³ – 2x + 1 est vrai, alors nous allons d’abord résoudre l’équation 2 = x – 1 et obtenir x = 3. Enfin, nous devrons substituer 3 à x, tel que 3³ – 2 · 3 + 1 = 22.
• Changement de variable : lorsqu’on a un polynôme P(x) = 4x – 2 et qu’on veut connaître cette valeur pour P(x + 2). Ensuite, nous devons changer tous les x de l’expression en a (x + 2). Cela dit, voyons à quoi ressemblerait ce dernier exemple résolu : P (x + 2) = 4 (x + 2) – 2.

Opérations avec des polynômes

Ci-dessous, nous expliquerons comment résoudre les quatre opérations arithmétiques de base avec des polynômes , en suivant toujours la hiérarchie des opérations . Dans chaque section, vous trouverez un peu de théorie qui vous permettra de savoir comment procéder dans chaque cas et quelques exemples pratiques.

addition de polynômes

Pour additionner des polynômes il faut tenir compte du fait qu’ils ne peuvent être regroupés que par des termes semblables , donc si on a les polynômes P(x) = 3x³ – x² + 2x – 4 et Q(x) = 2x² + 3x – 2. Alors pour faire P(x) + Q(x), on additionnera les coefficients des deux polynômes accompagnés du même exposant : P(x) + Q(x) = 3x³ + (-x) ² + 2x²) + (2x + 3x) + (-4 -2) = 3x³ + x² + 5x – 6. En résumé, nous pouvons dire que nous avons regroupé et additionné les coefficients de chaque terme similaire et au final nous avons exprimé tous les termes dans un seul polynôme.

soustraction de polynômes

La soustraction de polynômes se résout de la même manière que l’addition, la seule différence est évidemment le symbole. Ensuite, nous regroupons des termes similaires, soustrayons et transformons le tout en une seule expression. Ci-dessous, nous allons vous montrer à l’aide d’un exemple : P(x) = 5x³ – 2x² + x – 3 et Q(x) = 3x² + 5x + 4, puis P(x) – Q(x) = 5x³ + (-2x² + 3x²) + (x + 5x) + (-3 + 4) = 5x³ + x² + 6x + 1.

multiplication polynomiale

Lors de la résolution de ce type de multiplication, les choses peuvent devenir un peu compliquées, mais si vous suivez toutes les étapes dont nous vous parlerons, alors tout ira bien. Dans cette opération mathématique tous les monômes opéreront avec tous les autres, cela signifie que nous ne multiplierons pas seulement les termes semblables. De plus, non seulement les coefficients changeront , mais les exposants changeront également . Avec cet exemple vous comprendrez beaucoup mieux tout : P(x) = 2x² + 3x – 1 et Q(x) = 2x + 3 :

P(x) Q(x) = ( 2x² + 3x –1 ) · ( 2x + 3 ) = 2x² · 2x + 2x² · 3 + 3x · 2x + 3x · 3 + (-1 ) · 2x + (-1 ) · 3 = 4x³ + 6x² + 6x² + 9x – 2x – 3 = 4x³ + 12x² + 7x – 3

En gros, on multiplie les coefficients de chaque terme d’un polynôme par tous ceux du second puis on applique la propriété de puissance de a ⁿ · a ^m = a ^n+m .

division de polynômes

Enfin, nous n’avons qu’à expliquer comment résoudre la division des polynômes, en gros nous devons appliquer la propriété distributive de la division : (a + b + c) ÷ d = (a ÷ d) + (b ÷ d) + (c ÷ d). Et nous appliquerons également la propriété d’exponentiation suivante à ⁿ ÷ a ^m = a ^nm . Nous allons maintenant le voir avec un exemple simple : P(x) = 3x³ – 6x² + 9x et Q(x) = 3x.

P(x) ÷ Q(x) = ( 3x³ – 6x² +9x ) ÷ 3x = ( 3x³ ÷ 3x ) + ( 6x² ÷ 3x ) + (9x ÷ 3x ) = x² – 2x + 3

Maintenant que vous avez fini de voir comment résoudre toutes ces opérations avec des polynômes, nous espérons que vous savez comment l’appliquer en pratique. Mais si vous pensez que ce n’est pas le cas et que vous voulez continuer à pratiquer un peu, alors nous vous recommandons de regarder quelques exercices résolus sur cette page . Ceux-ci vous aideront à finir d’intérioriser tous ces concepts mathématiques.

Factorisation de polynômes

Pour factoriser des polynômes, vous pouvez le faire manuellement comme expliqué dans l’article de ce dernier lien ou vous pouvez le faire à l’aide d’une calculatrice Ruffini . Nous vous recommandons de le faire avec cette deuxième option si vous voulez le faire rapidement, mais si vous apprenez juste à factoriser, alors mieux vaut vous entraîner manuellement. La manière de le faire doit être choisie en fonction de votre situation.

Résolvez des polynômes avec la calculatrice scientifique

Il existe de nombreuses calculatrices scientifiques différentes sur le marché aujourd’hui. Mais si vous recherchez une calculatrice bon marché capable de résoudre des polynômes , nous vous recommandons la Casio FX-991SPX II . Il est facile à utiliser, très puissant et fonctionnel, ce qui le rend parfait pour tout étudiant en mathématiques au collège et au lycée. Ci-dessous, nous expliquerons brièvement comment les expressions mathématiques de ce style sont résolues à l’aide de ce modèle ou d’un modèle Casio similaire.

Il faut d’abord introduire la valeur numérique des variables, l’écrire puis appuyer sur « STO » + lettre de la variable , par exemple x. Ainsi, lorsque toutes les variables sont définies, il vous suffit d’écrire l’expression polynomiale telle quelle avec toutes les variables et tous les nombres. Et enfin, vous devez appuyer sur la touche égale, de cette façon vous obtiendrez le résultat équivalent à la valeur numérique du polynôme.