Dans cet article, nous expliquons quelles opérations peuvent être effectuées avec les fonctions. Vous pourrez voir l’explication ainsi que des exercices résolus sur les opérations avec les fonctions. Et enfin, vous retrouverez les propriétés des opérations avec les fonctions.
Que sont les opérations avec des fonctions ?
Vous pouvez effectuer 5 types d’opérations différents avec des fonctions : addition, soustraction, produit, division et composition. Autrement dit, deux fonctions peuvent être ajoutées, soustraites, multipliées, divisées ou composées.
Ensuite, nous allons voir comment chaque type d’opération est réalisé avec des fonctions et les caractéristiques de chacune d’elles.
Somme des fonctions
La valeur de la somme (ou de l’addition) de deux fonctions est égale à la somme de la valeur de chaque fonction. Autrement dit, pour calculer l’image d’une fonction somme, il suffit d’ajouter les images des fonctions impliquées dans l’opération.
![]()
De plus, le domaine de la somme de deux fonctions est l’intersection du domaine de chaque fonction sommée.
![]()
Voyons comment deux fonctions sont ajoutées à l’aide d’un exemple :
![]()
Nous ajoutons d’abord les deux fonctions :
![]()
Et maintenant nous trouvons le domaine de la fonction somme. Pour ce faire, nous calculons le domaine de chaque fonction séparément :
![]()
➤ Voir : comment calculer le domaine d’une fonction
Alors, le domaine de la fonction résultant de l’opération sera :
![]()
Chaque opération avec des fonctions doit être accompagnée de son domaine pour définir complètement le résultat.
Soustraction de fonctions
L’image de la soustraction (ou différence) de deux fonctions est la soustraction des images de chaque fonction participant à l’opération :
![]()
Comme pour la fonction d’addition, le domaine de soustraction de deux fonctions est équivalent à l’intersection du domaine de chaque fonction.
![]()
Ainsi, si une fonction n’est pas définie à une certaine valeur de la variable indépendante x, la fonction résultant de la soustraction ne le sera pas non plus.
Voyons comment deux fonctions sont soustraites à travers un exemple :
![]()
Nous soustrayons d’abord les deux fonctions :
![]()
Et puis on détermine le domaine de la fonction de soustraction :
![]()
![]()
Produit phare
Pour calculer le produit ou (la multiplication) de deux fonctions , il faut simplement multiplier les expressions de chaque fonction.
![]()
D’autre part, le domaine de la fonction produit est l’ensemble d’intersections du domaine de chaque fonction multipliée.
![]()
Par exemple, si nous avons les deux fonctions suivantes :
![]()
Tout d’abord, nous effectuons le fonctionnement du produit avec les deux fonctions :
![]()
Et, enfin, on trouve le domaine de la fonction résultant de l’opération :
![]()
![]()
Répartition des fonctions
Le résultat numérique d’une division (ou quotient) de deux fonctions correspond à l’équation suivante :
![]()
Cependant, le domaine de division de deux fonctions est l’ensemble des intersections du domaine de chaque fonction moins tous les x qui annulent la fonction qui fait office de diviseur, car sinon on obtiendrait une indétermination.
![]()
A titre d’exemple, nous allons diviser les fonctions suivantes :
![]()
La répartition des fonctions est la suivante :
![]()
D’autre part, le domaine de chaque fonction séparément est constitué de tous les nombres réels
![]()
Cependant, comme il ne peut pas y avoir de zéro au dénominateur d’une fraction, dans le domaine de la fonction résultante, nous devons supprimer toutes les valeurs qui annulent le dénominateur (x=3).
![]()
Composition des fonctions
La composition des fonctions est l’opération la plus difficile à résoudre, car c’est le concept le plus compliqué.
La composition des fonctions consiste en l’application successive de deux fonctions. Algébriquement, la composition de deux fonctions s’exprime comme suit :
![]()
D’autre part, le domaine de composition des fonctions
![]() est équivalent à l’ensemble de toutes les valeurs de x dans le domaine de la fonction
est équivalent à l’ensemble de toutes les valeurs de x dans le domaine de la fonction![]() tel que
tel que![]() appartient au domaine de la fonction
appartient au domaine de la fonction![]()
![]()
Par exemple, étant donné les deux fonctions suivantes :
![]()
Pour trouver la fonction composée
![]() suivi de
suivi de![]() nous devons remplacer l’expression de
nous devons remplacer l’expression de![]() où il y en a un
où il y en a un![]() dans l’expression de
dans l’expression de![]()
![Rendered by QuickLaTeX.com \begin{aligned}(g\circ f)(x)&=g\Bigl(f(x)\Bigr)\\[2ex]&= g\Bigl(x^2+1\Bigr)\\[2ex]&=3(x^2+1)-4\\[2ex]&=3x^2+3-4\\[2ex]&=3x^2-1\end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-f48079d61cf80409fdbf6610b5724189_l3.png)
Dans ce cas, le domaine des deux fonctions est entièrement constitué de nombres réels, donc le domaine de la fonction composite sera également constitué de nombres réels.
![]()
Comme vous pouvez le constater, la composition des fonctions n’est pas une opération simple à comprendre. C’est pourquoi nous vous recommandons de vous entraîner à faire les exercices suivants sur la composition des fonctions :
➤ Voir : exercices résolus sur la composition des fonctions
Propriétés des opérations avec des fonctions
De toutes les opérations avec fonctions, la somme et le produit se caractérisent par les propriétés suivantes :
- Propriété associative : l’ordre dans lequel 3 fonctions ou plus sont ajoutées ou multipliées est sans importance.
![]()
![]()
- Propriété commutative : l’ordre de l’addition ou de la multiplication de deux fonctions ne modifie pas le résultat.
![]()
![]()
- Élément neutre : l’opération somme et l’opération produit ont des fonctions constantes d’élément neutre
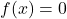 et
et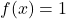 respectivement.
respectivement.
- Élément symétrique : la fonction somme a la fonction opposée
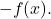
- Propriété distributive : cette propriété relie la somme et le produit des opérations, et repose sur l’égalité suivante :
![]()